3Dconfigurations/DescriptionOfRiemannTypeI

Description of Riemann Type I Ellipsoids

Type I Riemann Ellipsoids

An earlier, less succinct version of this chapter is titled, ThreeDimensionalConfigurations/DescriptionOfRiemannTypeI. Links to even earlier ramblings are provided below.

Analytic Determination of Equilibrium Model Parameters

Drawing heavily from §47 (pp. 129 - 132) of [EFE] , in a separate chapter we show how the steady-state 2^nd-order tensor virial equations can be used to derive the equilibrium structure of Riemann Ellipsoids of Type I, II, & III. By definition, for these types of Riemann Ellipsoids, the two vectors $\overrightarrow{\mathrm{\Omega }}$ and $\overrightarrow{\zeta }$ are not parallel to any of the principal axes of the ellipsoid, and they are not aligned with each other, but they both lie in the $y-z$ plane — that is to say, $({\mathrm{\Omega }}_1,{\zeta }_1)=(0,0)$. For a given specified density $(\rho )$ and choice of the three semi-axes $(a_1,a_2,a_3)\leftrightarrow (a,b,c)$, all five of the expressions displayed in that chapter's Summary Table must be used in order to determine the equilibrium configuration's associated values of the five unknowns: $\mathrm{\Pi },({\mathrm{\Omega }}_2,{\zeta }_2),({\mathrm{\Omega }}_3,{\zeta }_3)$.

STEP #1: Choose the trio of semi-axis lengths that will define the surface of a uniform-density ellipsoid. By definition, for Riemann Type I ellipsoids the choice must be restricted to the domain,

$a_2\ge a_1\ge a_3$	and	$2a_1\ge (a_2+a_3).$
BCO2004, Chapter X, §6, top of p. 186; English translation of Riemann (1861) [ EFE, Chapter 7, §51, Eq. (186) ]

STEP #2: Evaluate the integral expressions for the index symbols, $A_1$, $A_2$, and $A_3$, which will be used to evaluate the gravitational potential on the surface of, and throughout the interior of, the chosen ellipsoid. Because, for Type I ellipsoids, $a_2\ge a_1\ge a_3$, presumably we must adopt the associations, $(A_1,a_1)\leftrightarrow (A_m,a_m)$, $(A_2,a_2)\leftrightarrow (A_{\ell },a_{\ell })$, and $(A_3,a_3)\leftrightarrow (A_s,a_s).$ This means that the three most relevant index symbols are defined by the expressions,

$A_2$	$=$	$2\left(\frac{a_1}{a_2}\right)\left(\frac{a_3}{a_2}\right)\left[\frac{F(\theta ,k)-E(\theta ,k)}{k^2{\sin }^3\theta }\right],$
$A_3$	$=$	$2\left(\frac{a_1}{a_2}\right)\left[\frac{(a_1/a_2)\sin \theta -(a_3/a_2)E(\theta ,k)}{(1-k^2){\sin }^3\theta }\right],$
$A_1=2-(A_2+A_3)$	$=$	$\frac{2a_1{a}_3}{a_2^2}\left[\frac{E(\theta ,k)-(1-k^2)F(\theta ,k)-(a_3/a_1)k^2\sin \theta }{k^2(1-k^2){\sin }^3\theta }\right],$

where, the arguments of the incomplete elliptic integrals are,

$\theta ={\cos }^{-1}\left(\frac{a_3}{a_2}\right)$

and

$k=[\frac{1-(a_1/a_2{)}^2}{1-(a_3/a_2{)}^2}{]}^{1/2}.$

Note as well that,

$B_{23}$	$=$	$\left[\frac{A_2{a}_2^2-A_3{a}_3^2}{a_2^2-a_3^2}\right].$
[ EFE, Chapter 3, §21, Eqs. (105) & (107) ]

STEP #3: Switching notation from $(a_1,a_2,a_3)\to (a,b,c)$, evaluate the intermediary parameters, ${\beta }_{\pm }$ and ${\gamma }_{\pm }$:

$\beta$ $=$ $\frac{1}{4a^2}\{(4a^2-b^2+c^2)\mp [(4a^2+c^2-b^2{)}^2-16a^2{c}^2{]}^{1/2}\};$ [ EFE, Chapter 7, §47, Eq. (16) ] $\gamma$ $=$ $\frac{1}{4a^2}\{(4a^2+b^2-c^2)\mp [(4a^2+c^2-b^2{)}^2-16a^2{c}^2{]}^{1/2}\}.$ [ EFE, Chapter 7, §47, Eq. (17) ] As is emphasized in EFE (Chapter 7, §47, p. 131) "… the signs in front of the radicals, in the two expressions, go together. Furthermore, "the two roots … correspond to the fact that, consistent with Dedekind's theorem, two states of internal motions are compatible with the same external figure."

STEP #4: Using the following set of five constraint equations, determine the values of the five structural parameters, $\mathrm{\Pi }$, ${\mathrm{\Omega }}_2$, ${\zeta }_2$, ${\mathrm{\Omega }}_3$, and ${\zeta }_3$. The resulting parameter values will reflect the equilibrium properties of a "Direct" (Jacobi-like) configuration if $(\beta ,\gamma )\to ({\beta }_{+},{\gamma }_{+})$, whereas they will reflect the equilibrium properties of the "Adjoint" (Dedekind-like) configuration if $(\beta ,\gamma )\to ({\beta }_{-},{\gamma }_{-})$.

$\left[\frac{3\cdot 5}{2\pi (abc)\rho }\right]\mathrm{\Pi }$

$=$

$4\pi G\rho c^2\{A_3+[\frac{a^2(3b^2-4a^2+c^2)B_{23}+b^2(a^2{A}_1-c^2{A}_3)}{4a^4-a^2(b^2+c^2)+b^2{c}^2}\left]\right\};$

$0$	$=$	$\beta \left(\frac{{\mathrm{\Omega }}_2^2}{\pi G\rho }\right)\left[\frac{c^2-b^2}{4c^2}\right][4a^4-a^2(b^2+c^2)+b^2{c}^2]+[a^2(3b^2-4a^2+c^2)B_{23}+b^2(a^2{A}_1-c^2{A}_3)];$
[ EFE, Chapter 7, §51, Eq. (170) ]

${\zeta }_2$	$=$	$-{\mathrm{\Omega }}_2\beta \left[\frac{a^2+c^2}{c^2}\right];$
[ EFE, Chapter 7, §47, Eq. (12) ]

$0$	$=$	$-\gamma \left(\frac{{\mathrm{\Omega }}_3^2}{\pi G\rho }\right)\left[\frac{c^2-b^2}{4b^2}\right][4a^4-a^2(b^2+c^2)+b^2{c}^2]+[a^2(b^2+3c^2-4a^2)B_{23}+c^2(a^2{A}_1-b^2{A}_2)];$
[ EFE, Chapter 7, §51, Eq. (171) ]

${\zeta }_3$	$=$	$-{\mathrm{\Omega }}_3\gamma \left[\frac{a^2+b^2}{b^2}\right].$
[ EFE, Chapter 7, §47, Eq. (12) ]

Maclaurin Spheroid Limit

Basic Relations

In Chapter 7, §51(c) (pp. 165 - 166) of [EFE] , Chandrasekhar shows that "… the entire Maclaurin sequence can be considered as limiting $(a_2/a_1\to 1)$ forms of the Riemann Ellipsoids of type I." First, we recall that, as viewed from the inertial frame, each Maclaurin spheroid of eccentricity, $e=(1-a_3^2/a_1^2{)}^{1/2}$, rotates uniformly with angular velocity,

${\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}^2\equiv \frac{{\omega }_0^2}{\pi G\rho }=2e^2{B}_{13}$	$=$	$2(3-2e^2)(1-e^2{)}^{1/2}\cdot \frac{{\sin }^{-1}e}{e^3}-\frac{6(1-e^2)}{e^2}.$
[EFE], §32, pp. 77-78, Eqs. (4) & (6)

Given the specified value of the semi-axis ratio, $a_3/a_1$, the properties of the limiting Riemann Type I ellipsoid are given by the expressions,

$2{\mathrm{\Omega }}_3$	$=$	${\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}\pm [16B_{13}+{\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}^2{]}^{1/2},$
[EFE], Chapter 7, §51(c), p. 166, Eq. (215)

and,

${\zeta }_3$	$=$	$2({\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}-{\mathrm{\Omega }}_3),$
[EFE], Chapter 7, §51(c), p. 165, Eq. (212)

where,

$B_{13}$	$=$	$\left[\frac{A_1{a}_1^2-A_3{a}_3^2}{a_1^2-a_3^2}\right];$
[EFE], Chapter 3, §21, Eqs. (105) & (107)

and,

$A_1$	$=$	$\frac{1}{e^2}[\frac{{\sin }^{-1}e}{e}-(1-e^2{)}^{1/2}](1-e^2{)}^{1/2},$
$A_3$	$=$	$\frac{2}{e^2}[(1-e^2{)}^{-1/2}-\frac{{\sin }^{-1}e}{e}](1-e^2{)}^{1/2}.$
[EFE], §17, p. 43, Eq. (36)

REMINDER:  For a given choice of the eccentricity, there are two viable solutions … the direct configuration and its adjoint. In the context of Riemann S-type ellipsoids, this pair of solutions arises from the choice of the sign $(\pm )$ in the expression for ${\mathrm{\Omega }}_3$; in the context of Type I Riemann ellipsoids (i.e., here) the pair arises from the choice of the sign $(\mp )$ in the STEP #3 determination of $\beta$ and $\gamma$. In both physical contexts, the direct (Jacobi-like) solution results from selecting the inferior sign while the adjoint (Dedekind-like) solution results from selecting the superior sign.

Frequency Ratio

In the context of Riemann S-type ellipsoids, we have found it useful to examine model sequences along which the frequency ratio,

$f$

$\equiv$

$\frac{{\zeta }_3}{{\mathrm{\Omega }}_3},$

is constant. Below, we will examine how such sequences behave across the domain of Type I Riemann Ellipsoids. In anticipation of this discussion, here we examine how $f$ varies along the limiting Maclaurin spheroid sequence.

Adopting the parameter,

${\mathscr{H}}\equiv \frac{16B_{13}}{{\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}^2}$

$=$

$\frac{8}{e^2}$

we have the relation,

$\frac{2{\mathrm{\Omega }}_3}{{\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}}$

$=$

$1\pm (1+{\mathscr{H}}{)}^{1/2}.$

But we also see that,

$f_{\mathrm{M}\mathrm{c}}=(\frac{{\zeta }_3}{{\mathrm{\Omega }}_3}{)}_{\mathrm{M}\mathrm{c}}$

$=$

$2[\frac{{\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}}{{\mathrm{\Omega }}_3}-1].$

Combining these last two expressions gives,

$\frac{4}{f_{\mathrm{M}\mathrm{c}}+2}$	$=$	$1\pm (1+{\mathscr{H}}{)}^{1/2}$
	$=$	$1\pm [1+\frac{8}{e^2}{]}^{1/2}$
$\Rightarrow \frac{4e}{f_{\mathrm{M}\mathrm{c}}+2}$	$=$	$e\pm (8+e^2{)}^{1/2}$
$\Rightarrow f_{\mathrm{M}\mathrm{c}}$	$=$	$4e[e\pm (8+e^2{)}^{1/2}{]}^{-1}-2.$

In an accompanying discussion of the Maclaurin spheroid sequence, a number of different plots have been used to display how various physical parameters vary along the sequence. The solid curve that appears in Figure 1 of that discussion has been redrawn as a black-dotted curve in the left-hand panel of Figure 1 of this chapter (immediately below); it shows how ${\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}^2$ varies with the spheroid's eccentricity, $e$. The small solid-green square marker identifies the location along the sequence where the system with the maximum angular velocity resides:

$[e,\frac{{\omega }_0^2}{\pi G\rho }]$	$\equiv$	$[0.92995,0.449331].$
[EFE], §32, p. 80, Eqs. (9) & (10)

Figure 1:   Parameter Variations Along the Maclaurin Spheroid Sequence
JacobiSequenceToo	FrequencyRatio
Analogous to Figure 5 from §32, p. 79 of [EFE]; shows how the square of the normalized rotation frequency varies with eccentricity, $e=(1-a_3/a_1{)}^{1/2},$ along the (black-dotted) Maclaurin sequence and along the Jacobi sequence (series of purple circular markers).

Note:	$e$	${\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}^2$		Limiting Riemann S-type Ellipsoids					Limiting Type I Riemann Ellipsoids
				Direct		Adjoint			Direct		Adjoint
				${\mathrm{\Omega }}_3^2$	$f=\frac{{\zeta }_3}{{\mathrm{\Omega }}_3}$	$({\mathrm{\Omega }}_3^{†}{)}^2$	$f^{†}=\frac{{\zeta }_3^{†}}{{\mathrm{\Omega }}_3^{†}}$		${\mathrm{\Omega }}_3^2$	$f=\frac{{\zeta }_3}{{\mathrm{\Omega }}_3}$	$({\mathrm{\Omega }}_3^{†}{)}^2$	$f^{†}=\frac{{\zeta }_3^{†}}{{\mathrm{\Omega }}_3^{†}}$
(a)	0.00000	0.00000		000	000	000	000		000	000	000	000
(b)	0.81267	0.37423		000	000	000	000		000	000	000	000
(c)	0.92995	0.44933		000	000	000	000		000	000	000	000
(d)	0.95289	0.44022		000	000	000	000		000	000	000	000
Notes: Nonrotating sphere, $c/a\to 1$; also, self-adjoint Riemann S-type ellipsoid Bifurcation to Jacobi (direct) and Dedekind (adjoint) sequences Configuration with maximum ${\mathrm{\Omega }}_{\mathrm{M}\mathrm{c}}^2$ Onset of dynamical instability; also, self-adjoint Riemann S-type ellipsoid Infinitesimally thin disk, $c/a\to 0$

Example Equilibrium Models

Riemann S-Type Ellipsoids	Type I Riemann Ellipsoids
EFE Figure 17

Extracted from Table 4 of XXVIII

Here are equilibrium model parameters drawn from Table 4 of 📚 S. Chandrasekhar (1966, ApJ, Vol. 145, pp. 842 - 877) — referred to in [EFE] as Publication XXVIII.

Data Extracted from Table 4 (p. 858) of S. Chandrasekhar (1966) The Equilibrium and the Stability of the Riemann Ellipsoids. II. The Astrophysical Journal, Vol. 145, pp. 842 - 877																Our (reverse-engineered) Determination of Index Symbols
The Properties of a Few Riemann Ellipsoids of Type I
$\frac{a_2}{a_1}$	$\frac{a_3}{a_1}$		Direct							Adjoint						A1	A2	A3
			${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\zeta }_2$	${\zeta }_3$	$({\zeta }_2/{\mathrm{\Omega }}_2)$	$({\zeta }_3/{\mathrm{\Omega }}_3)$		${\mathrm{\Omega }}_2^{†}$	${\mathrm{\Omega }}_3^{†}$	${\zeta }_2^{†}$	${\zeta }_3^{†}$	$({\zeta }_2/{\mathrm{\Omega }}_2{)}^{†}$	$({\zeta }_3/{\mathrm{\Omega }}_3{)}^{†}$
1.05263	0.41667		+0.14834	+0.73257	-1.41355	-2.61578	-9.52912	-3.57069		+0.50185	+1.30617	-0.41783	-1.46707	-0.83258	-1.12318	0.43008706	0.40190235	1.16801059
1.25000	0.50000		+0.39259	+0.66536	-2.19983	-1.93895	-5.60338	-2.91414		+0.87993	+0.94583	-0.98148	-1.36398	-1.11541	-1.44210	0.50823343	0.37944073	1.11232585
1.44065	0.49273		+0.57179	+0.59896	-2.24560	-1.49425	-3.92732	-2.49474		+0.89032	+0.69996	-1.44219	-1.27866	-1.61986	-1.82676	0.52403947	0.32351421	1.15244632
1.66667	0.33333		+0.71251	+0.52815	-2.37502	-1.19714	-3.33331	-2.26667		+0.71251	+0.52815	-2.37502	-1.19714	-3.33331	-2.26667	0.41805282	0.20718125	1.37476593
1.36444	0.09518		+0.05632	+0.40707	-6.68275	-1.24612	-118.657	-3.06119		+0.63035	+0.59414	-0.59714	-0.85376	-0.94731	-1.43697	0.14374587	0.09152713	1.76472699
1.69351	0.11813		+0.15764	+0.38504	-6.27092	-1.02536	-39.7800	-2.66300		+0.73061	+0.44893	-1.35309	-0.87944	-1.85200	-1.95897	0.18178501	0.08464699	1.73356799
1.52303	0.05315		+0.03311	+0.29600	-9.85239	-0.84580	-297.565	-2.85743		+0.52221	+0.38805	-0.62474	-0.64518	-1.19634	-1.66262	0.08593434	0.04618515	1.86788051
1.78590	0.06233		+0.08952	+0.28558	-9.19424	-0.74657	-102.706	-2.61422		+0.57083	+0.31825	-1.4418	-0.66992	-2.52580	-2.10501	0.10258739	0.04358267	1.85382994
NOTE:   All frequencies are given in the unit of $(\pi G\rho {)}^{1/2}$.

Given the values of ${\mathrm{\Omega }}_2$ and ${\mathrm{\Omega }}_3$ from this table, we have reverse-engineered this problem and determined what numerical values of $A_1$, $A_2$, and $A_3$ were used by 📚 Chandrasekhar (1966; XXVIII) for various models. These values have been recorded in the last three columns of the table.

Extracted from Table 6a of XXVIII

Data Extracted from Table 6a (p. 871) of S. Chandrasekhar (1966) The Equilibrium and the Stability of the Riemann Ellipsoids. II. The Astrophysical Journal, Vol. 145, pp. 842 - 877   [ Also appears as Table XIII(a) on p. 170 of EFE ]												Our (reverse-engineered) Determination of Index Symbols
The Properties of Marginally Overstable Riemann Ellipsoids of Type I
$\frac{a_2}{a_1}$	$\frac{a_3}{a_1}$		Direct					Adjoint				A1	A2	A3
			${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\zeta }_2$	${\zeta }_3$		${\mathrm{\Omega }}_2^{†}$	${\mathrm{\Omega }}_3^{†}$	${\zeta }_2^{†}$	${\zeta }_3^{†}$
1.0000	0.3033		0.0000	+0.7073	0.0000	-2.7417		0.0000	+1.3708	0.0000	-1.4147	0.341295655	0.341295655	1.317408690
1.0526	0.3712		+0.1283	+0.7176	-1.5014	-2.5977		+0.4898	+1.2972	-0.3931	-1.4371	0.39892471	0.37240741	1.22866788
1.1111	0.4230		+0.2153	+0.7098	-1.8984	-2.3978		+0.6812	+1.1922	-0.6000	-1.4275	0.44194613	0.38437206	1.17368182
1.1765	0.4560		+0.2942	+0.6901	-2.1276	-2.1787		+0.8032	+1.0751	-0.7794	-1.3984	0.47156283	0.38075039	1.14768677
1.2500	0.4703		+0.3639	+0.6633	-2.2794	-1.9637		+0.8778	+0.9579	-0.9450	-1.3599	0.48950275	0.36484494	1.14565231
1.3333	0.4676		+0.4269	+0.6329	-2.3842	-1.7621		+0.9150	+0.8458	-1.1125	-1.3186	0.49697204	0.33963373	1.16339423
1.4286	0.4474		+0.4877	+0.5999	-2.4626	-1.5752		+0.9178	+0.7400	-1.3082	-1.2768	0.49205257	0.30602987	1.20191756
1.5385	0.4053		+0.5550	+0.5635	-2.5307	-1.3984		+0.8807	+0.6390	-1.5937	-1.2330	0.47004307	0.26291500	1.26704192
1.6722	0.3278		+0.7107	+0.5142	-2.4011	-1.1673		+0.7107	+0.5142	-2.4011	-1.1673	0.42132864	0.19910085	1.37957051
NOTE:   All frequencies are given in the unit of $(\pi G\rho {)}^{1/2}$. Also … The model highlighted with a light-blue background is a Maclaurin spheroid; in this case we determined the values of the index symbols, $A_1$, $A_2$, and $A_3$, from the analytic expressions given in our accompanying discussion of the gravitational potential of oblate spheroids. The model highlighted with a yellow background is the example that we have used elsewhere in this MediaWiki chapter to illustrate the trajectories of Lagrangian fluid elements. The model whose frequencies have been highlighted with a pink background appears to be self-adjoint.

Extracted from Table 6b of XXVIII

Data Extracted from Table 6b (p. 871) of S. Chandrasekhar (1966) The Equilibrium and the Stability of the Riemann Ellipsoids. II. The Astrophysical Journal, Vol. 145, pp. 842 - 877   [ Also appears as Table XIII(b) on p. 170 of EFE ]												Our (reverse-engineered) Determination of Index Symbols
The Properties of Marginally Overstable Riemann Ellipsoids of Type I
$\frac{a_2}{a_1}$	$\frac{a_3}{a_1}$		Direct					Adjoint				A1	A2	A3
			${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\zeta }_2$	${\zeta }_3$		${\mathrm{\Omega }}_2^{†}$	${\mathrm{\Omega }}_3^{†}$	${\zeta }_2^{†}$	${\zeta }_3^{†}$
1.1582	0.1411		+0.0618	+0.5209	-4.1927	-1.8047		+0.5802	+0.8927	-0.4469	-1.053	0.19506141	0.15833429	1.64660480
1.1846	0.1238		+0.0558	+0.4903	-4.7796	-1.6695		+0.5829	+0.8229	-0.4573	-0.9947	0.17573713	0.13759829	1.68666459
1.2124	0.1057		+0.0480	+0.4554	-5.4901	-1.5236		+0.5737	+0.7479	-0.4598	-0.9277	0.12951075	0.09436674	1.77612251
1.2418	0.0866		+0.0389	+0.4146	-6.4045	-1.3629		+0.5506	+0.6658	-0.4523	-0.8488	0.12951075	0.09436674	1.77612251
1.2727	0.0666		+0.0286	+0.3658	-7.6880	-1.1810		+0.5098	+0.5737	-0.4308	-0.7529	0.1025817	0.07183867	1.82557964
1.3050	0.0455		+0.0176	+0.3044	-9.7572	-0.9654		+0.4436	+0.4661	-0.3873	-0.6305	0.07218729	0.04860482	1.87920789
1.3707	ε		+2.1492 ε3/2	+1.4485 ε1/2	-2.2795 ε-1/2	-4.4390 ε1/2		+2.2795 ε1/2	+2.1135 ε1/2	-2.1492 ε1/2	-3.0422 ε1/2	---	---	---
NOTE:   All frequencies are given in the unit of $(\pi G\rho {)}^{1/2}$.

Extracted from Table 6c of XXVIII

Data Extracted from Table 6c (p. 872) of S. Chandrasekhar (1966) The Equilibrium and the Stability of the Riemann Ellipsoids. II. The Astrophysical Journal, Vol. 145, pp. 842 - 877   [ Also appears as Table XIII(c) on p. 170 of EFE ]												Our (reverse-engineered) Determination of Index Symbols
The Properties of Marginally Overstable Riemann Ellipsoids of Type I
$\frac{a_2}{a_1}$	$\frac{a_3}{a_1}$		Direct					Adjoint				A1	A2	A3
			${\mathrm{\Omega }}_2$	${\mathrm{\Omega }}_3$	${\zeta }_2$	${\zeta }_3$		${\mathrm{\Omega }}_2^{†}$	${\mathrm{\Omega }}_3^{†}$	${\zeta }_2^{†}$	${\zeta }_3^{†}$
1.2907	0.1573		+0.0979	+0.5082	-4.6947	-1.6093		+0.7206	+0.7791	-0.6376	-1.0498	0.21984120	0.15276149	1.62739731
1.4954	0.1563		+0.1427	+0.4633	-5.1812	-1.3221		+0.7908	+0.6109	-0.9355	-1.0027	0.22570513	0.12700933	1.64728554
1.6417	0.1431		+0.1769	+0.4219	-5.5580	-1.1381		+0.7788	+0.5056	-1.2612	-0.9496	0.21358447	0.10455951	1.68185603
1.7679	0.1233		+0.2211	+0.3784	-6.0132	-0.9802		+0.7280	+0.4200	-1.8137	-0.8829	0.19209450	0.08326199	1.72464351
1.8651	0.0976		+0.2856	+0.3310	-6.7416	-0.8341		+0.6299	+0.3471	-2.8546	-0.7942	0.16820821	0.06283471	1.76895708
NOTE:   All frequencies are given in the unit of $(\pi G\rho {)}^{1/2}$.

Examination of Lagrangian Flow

EFE Rotating Cartesian Frame

Concentric triaxial ellipsoids are defined by the expression,

$P$

$=$

$(\frac{x}{a}{)}^2+(\frac{y}{b}{)}^2+(\frac{z}{c}{)}^2,$

where $0\le P\le 1$ is a constant. As viewed from the rotating reference frame, the velocity flow-field everywhere inside $(0\le P<1)$, and on the surface $(P=1)$ of the Type I Riemann ellipsoid is given by the expression — see, for example, an accompanying discussion of the Riemann flow-field,

${\mathbf{𝐮}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

$=$

$\hat{\mathit{ı}}\{-[\frac{a^2}{a^2+b^2}]{\zeta }_{3}y+[\frac{a^2}{a^2+c^2}\left]{\zeta }_{2}z\right\}+\hat{\mathit{ȷ}}\{+[\frac{b^2}{a^2+b^2}\left]{\zeta }_{3}x\right\}+\hat{\mathbf{k}}\{-[\frac{c^2}{a^2+c^2}\left]{\zeta }_{2}x\right\}.$

In an accompanying discussion, we have shown that,

${\mathbf{𝐮}}_{\mathrm{E}\mathrm{F}\mathrm{E}}\cdot \mathrm{\nabla }P$

$=$

$0,$

which means that, at every location inside and on the surface of the configuration, the velocity vector is orthogonal to a vector that is normal to the ellipsoidal surface at that location.

Tilted Coordinate System

Figure 1:   Tilted Reference Frame
$\hat{\mathit{ı}}$ $\to$ ${\hat{\mathit{ı}}}^{\prime },$ $\hat{\mathit{ȷ}}$ $\to$ ${\hat{\mathit{ȷ}}}^{\prime }\cos \theta -{\hat{\mathit{k}}}^{\prime }\sin \theta ,$ $\hat{\mathit{k}}$ $\to$ ${\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathit{k}}}^{\prime }\cos \theta .$		$x$ $\to$ $x^{\prime },$ $y$ $\to$ $y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$ $z-z_0$ $\to$ $y^{\prime }\sin \theta +z^{\prime }\cos \theta .$

As we have detailed in our accompanying discussion, as viewed from this "tipped" frame, the concentric ellipsoidal surfaces of a Type I Riemann ellipsoid are defined by the expression,

$P^{\prime }$

$=$

$[\frac{y^{\prime }\cos \theta -z^{\prime }\sin \theta }{b}{]}^2+[\frac{z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta }{c}{]}^2+(\frac{x^{\prime }}{a}{)}^2.$

and the velocity flow-field is given by the expression,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{\prime }\{-[\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )\}$
		$+[{\hat{\mathit{ȷ}}}^{\prime }\cos \theta -{\hat{\mathbf{k}}}^{\prime }\sin \theta ]\left\{\right[\frac{b^2}{a^2+b^2}\left]{\zeta }_3{x}^{\prime }\right\}+[{\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathbf{k}}}^{\prime }\cos \theta ]\{-[\frac{c^2}{a^2+c^2}\left]{\zeta }_2{x}^{\prime }\right\}$
	$=$	${\hat{\mathit{ı}}}^{\prime }\{-[\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )\}$
		$+{\hat{\mathit{ȷ}}}^{\prime }\{\cos \theta [\frac{b^2}{a^2+b^2}]{\zeta }_3-\sin \theta [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}{x}^{\prime }-{\hat{\mathbf{k}}}^{\prime }\{\sin \theta [\frac{b^2}{a^2+b^2}]{\zeta }_3+\cos \theta [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}{x}^{\prime }.$

We also have explicitly demonstrated that, for any arbitrarily chosen value of the tilt angle, $\theta$,

${{\mathbf{𝐮}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}\cdot \mathrm{\nabla }{P}^{\prime }$

$=$

$0.$

Preferred Tilt

As we discuss elsewhere, if we specifically choose,

$\tan \theta$

$=$

$-\frac{\beta {\mathrm{\Omega }}_2}{\gamma {\mathrm{\Omega }}_3}=-\left[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\right]\frac{{\zeta }_2}{{\zeta }_3},$

the component of the flow-field in the ${\hat{\mathbf{k}}}^{\prime }$ direction vanishes; that is, in this specific case, as viewed from the tilted reference frame, all of the fluid motion is confined to the x'-y' plane. Notice that this plane is not parallel to any of the three principal planes of the Type I Riemann ellipsoid. I have not seen this fluid-flow behavior previously described in the published literature. Maybe Norman Lebovitz will know.

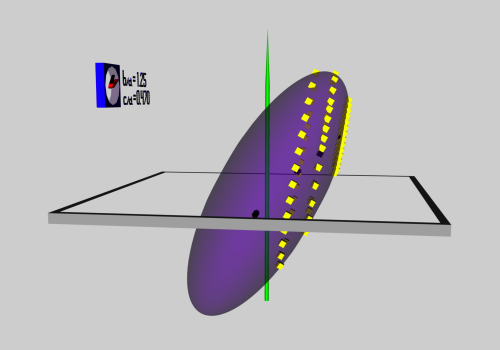
The three panels of Figure 2, and the text description that follows, have been drawn from a separate discussion.

Figure 2a	Figure 2b
↲
Figure 2c
↲

As has been described in an accompanying discussion of Riemann Type 1 ellipsoids, we have used COLLADA to construct an animated and interactive 3D scene that displays in purple the surface of an example Type I ellipsoid; panels a and b of Figure 2 show what this ellipsoid looks like when viewed from two different perspectives. (As a reminder — see the explanation accompanying Figure 2 of that accompanying discussion — the ellipsoid is tilted about the x-coordinate axis at an angle of 61.25° to the equilibrium spin axis, which is shown in green.) Yellow markers also have been placed in this 3D scene at each of the coordinate locations specified in the table that accompanies that discussion. From the perspective presented in Figure 2b, we can immediately identify three separate, nearly circular trajectories; the largest one corresponds to our choice of z₀ = -0.25, the smallest corresponds to our choice of z₀ = -0.60, and the one of intermediate size correspond to our choice of z₀ = -0.4310. When viewed from the perspective presented in Figure 2a, we see that these three trajectories define three separate planes; each plane is tipped at an angle of θ = -19.02° to the untilted equatorial, x-y plane of the purple ellipsoid.

Vorticity

Here we examine the expression for the vorticity from several different coordinate-system orientations.

wrt Rotating Body Frame

As provided above, the steady-state velocity field as viewed from the rotating ellipsoid's body frame is,

${\mathbf{𝐮}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

$=$

$\hat{\mathit{ı}}\{-[\frac{a^2}{a^2+b^2}]{\zeta }_{3}y+[\frac{a^2}{a^2+c^2}\left]{\zeta }_{2}z\right\}+\hat{\mathit{ȷ}}\{+[\frac{b^2}{a^2+b^2}\left]{\zeta }_{3}x\right\}+\hat{\mathbf{k}}\{-[\frac{c^2}{a^2+c^2}\left]{\zeta }_{2}x\right\}.$

Hence, as viewed with respect to the body frame, we find,

$\mathrm{\nabla }\times {\mathit{u}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$\equiv$	$\hat{\mathit{ı}}\{\frac{\partial u_z}{\partial y}-\frac{\partial u_y}{\partial z}\}+\hat{\mathit{ȷ}}\{\frac{\partial u_x}{\partial z}-\frac{\partial u_z}{\partial x}\}+\hat{\mathit{k}}\{\frac{\partial u_y}{\partial x}-\frac{\partial u_x}{\partial y}\}$
	$=$	$\hat{\mathit{ȷ}}\left\{\right[\frac{a^2}{a^2+c^2}]{\zeta }_2+[\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}+\hat{\mathit{k}}\left\{\right[\frac{b^2}{a^2+b^2}]{\zeta }_3+[\frac{a^2}{a^2+b^2}\left]{\zeta }_3\right\}$
	$=$	$\hat{\mathit{ȷ}}{\zeta }_2+\hat{\mathit{k}}{\zeta }_3.$

Another Choice

Now let's view the flow from a "tilted plane" in which the vorticity vector aligns with the ${\hat{\mathit{k}}}^{″}$ axis.

${{\mathit{u}}^{″}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{″}\{-[\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{″}\cos \chi -z^{″}\sin \chi )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(z_0+y^{″}\sin \chi +z^{″}\cos \chi )\}$
		$+{\hat{\mathit{ȷ}}}^{″}\{\cos \chi [\frac{b^2}{a^2+b^2}]{\zeta }_3-\sin \chi [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}{x}^{″}-{\hat{\mathbf{k}}}^{″}\{\sin \chi [\frac{b^2}{a^2+b^2}]{\zeta }_3+\cos \chi [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}{x}^{″}.$

The vorticity is,

$\mathrm{\nabla }\times {{\mathit{u}}^{″}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$\equiv$	${\hat{\mathit{ı}}}^{″}\{\frac{\partial {u_z}^{″}}{\partial y^{″}}-\frac{\partial {u_y}^{″}}{\partial z^{″}}\}+{\hat{\mathit{ȷ}}}^{″}\{\frac{\partial {u_x}^{″}}{\partial z^{″}}-\frac{\partial {u_z}^{″}}{\partial x^{″}}\}+{\hat{\mathit{k}}}^{″}\{\frac{\partial {u_y}^{″}}{\partial x^{″}}-\frac{\partial {u_x}^{″}}{\partial y^{″}}\}$
	$=$	${\hat{\mathit{ȷ}}}^{″}\left\{\right[\frac{a^2}{a^2+b^2}]{\zeta }_3(\sin \chi )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(\cos \chi )\}+{\hat{\mathit{ȷ}}}^{″}\{\sin \chi [\frac{b^2}{a^2+b^2}]{\zeta }_3+\cos \chi [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}$
		$+{\hat{\mathit{k}}}^{″}\{\cos \chi [\frac{b^2}{a^2+b^2}]{\zeta }_3-\sin \chi [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}+{\hat{\mathit{k}}}^{″}\left\{\right[\frac{a^2}{a^2+b^2}]{\zeta }_3(\cos \chi )-[\frac{a^2}{a^2+c^2}]{\zeta }_2(\sin \chi )\}$
	$=$	${\hat{\mathit{ȷ}}}^{″}\left\{\right[\frac{a^2}{a^2+b^2}+\frac{b^2}{a^2+b^2}]{\zeta }_3(\sin \chi )+[\frac{a^2}{a^2+c^2}+\frac{c^2}{a^2+c^2}]{\zeta }_2(\cos \chi )\}$
		$+{\hat{\mathit{k}}}^{″}\left\{\right[\frac{a^2}{a^2+b^2}+\frac{b^2}{a^2+b^2}]{\zeta }_3(\cos \chi )-[\frac{a^2}{a^2+c^2}+\frac{c^2}{a^2+c^2}]{\zeta }_2(\sin \chi )\}$
	$=$	${\hat{\mathit{ȷ}}}^{″}\{{\zeta }_3(\sin \chi )+{\zeta }_2(\cos \chi )\}+{\hat{\mathit{k}}}^{″}\{{\zeta }_3(\cos \chi )-{\zeta }_2(\sin \chi )\}$
	$=$	${\hat{\mathit{ȷ}}}^{″}\{\tan \chi +\frac{{\zeta }_2}{{\zeta }_3}\}{\zeta }_3\cos \chi +{\hat{\mathit{k}}}^{″}\{1-\frac{{\zeta }_2}{{\zeta }_3}\tan \chi \}{\zeta }_3\cos \chi .$

So, in order for the ${\hat{\mathit{ȷ}}}^{″}$ component to be zero, we choose,

$\tan \chi$	$=$	$-\frac{{\zeta }_2}{{\zeta }_3},$
$\Rightarrow \cos \chi$	$=$	$[1+\frac{{\zeta }_2^2}{{\zeta }_3^2}{]}^{-1/2},$

in which case we have,

$\mathrm{\nabla }\times {{\mathit{u}}^{″}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{k}}}^{″}\{1+\frac{{\zeta }_2^2}{{\zeta }_3^2}\}{\zeta }_3[1+\frac{{\zeta }_2^2}{{\zeta }_3^2}{]}^{-1/2}$
	$=$	${\hat{\mathit{k}}}^{″}[1+\frac{{\zeta }_2^2}{{\zeta }_3^2}{]}^{1/2}{\zeta }_3$
	$=$	${\hat{\mathit{k}}}^{″}({\zeta }_2^2+{\zeta }_3^2{)}^{1/2}.$

This makes sense!

Now, can we retrieve the "rotating body frame" expression simply by transforming the coordinates? Well …

${\hat{\mathit{k}}}^{″}$	$=$	$-\hat{\mathit{ȷ}}\sin \chi +\hat{\mathit{k}}\cos \chi$
$\Rightarrow \mathrm{\nabla }\times {{\mathit{u}}^{″}}_{\mathrm{E}\mathrm{F}\mathrm{E}}={\hat{\mathit{k}}}^{″}{\zeta }_3$	$=$	$({\zeta }_2^2+{\zeta }_3^2{)}^{1/2}[-\hat{\mathit{ȷ}}\sin \chi +\hat{\mathit{k}}\cos \chi ]$
	$=$	$({\zeta }_2^2+{\zeta }_3^2{)}^{1/2}[-\hat{\mathit{ȷ}}\tan \chi +\hat{\mathit{k}}]\cos \chi$
	$=$	$({\zeta }_2^2+{\zeta }_3^2{)}^{1/2}[\hat{\mathit{ȷ}}\left(\frac{{\zeta }_2}{{\zeta }_3}\right)+\hat{\mathit{k}}\left]\right[1+\frac{{\zeta }_2^2}{{\zeta }_3^2}{]}^{-1/2}$
	$=$	$\hat{\mathit{ȷ}}{\zeta }_2+\hat{\mathit{k}}{\zeta }_3.$

Hooray!

wrt Lagrangian Orbital Planes

As viewed from the "preferred tilted plane," the steady-state velocity field is,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{\prime }\{-[\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )\}$
		$+{\hat{\mathit{ȷ}}}^{\prime }\{\cos \theta [\frac{b^2}{a^2+b^2}]{\zeta }_3-\sin \theta [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}{x}^{\prime }-{\hat{\mathit{k}}}^{\prime }{\xcancel{\{\tan \theta [\frac{b^2}{a^2+b^2}]{\zeta }_3+[\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}}}^0\cos \theta x^{\prime }$

where,

$\tan \theta$

$=$

$-\frac{\beta {\mathrm{\Omega }}_2}{\gamma {\mathrm{\Omega }}_3}=-\left[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\right]\frac{{\zeta }_2}{{\zeta }_3}.$

Hence, the vorticity is,

$\mathrm{\nabla }\times {{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	$-{\hat{\mathit{ı}}}^{\prime }\left\{\frac{\partial u{\text{'}}_y}{\partial z^{\prime }}\right\}+{\hat{\mathit{ȷ}}}^{\prime }\left\{\frac{\partial u{\text{'}}_x}{\partial z^{\prime }}\right\}+{\hat{\mathit{k}}}^{\prime }\{\frac{\partial u{\text{'}}_y}{\partial x^{\prime }}-\frac{\partial u{\text{'}}_x}{\partial y^{\prime }}\}$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }\frac{\partial }{\partial z^{\prime }}\left\{\right[\frac{a^2}{a^2+b^2}]{\zeta }_3(z^{\prime }\sin \theta )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(z^{\prime }\cos \theta )\}$
		$+{\hat{\mathit{k}}}^{\prime }\frac{\partial }{\partial x^{\prime }}\{x^{\prime }\cos \theta [\frac{b^2}{a^2+b^2}]{\zeta }_3-x^{\prime }\sin \theta [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}+{\hat{\mathit{k}}}^{\prime }\frac{\partial }{\partial y^{\prime }}\left\{\right[\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }\cos \theta )-[\frac{a^2}{a^2+c^2}]{\zeta }_2(y^{\prime }\sin \theta )\}$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{a^2}{a^2+b^2}]{\zeta }_3\tan \theta +[\frac{a^2}{a^2+c^2}\left]{\zeta }_2\right\}\cos \theta +{\hat{\mathit{k}}}^{\prime }\left\{\right[\frac{b^2}{a^2+b^2}]{\zeta }_3-\tan \theta [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}\cos \theta +{\hat{\mathit{k}}}^{\prime }\left\{\right[\frac{a^2}{a^2+b^2}]{\zeta }_3-[\frac{a^2}{a^2+c^2}]{\zeta }_2\tan \theta \}\cos \theta$

$\Rightarrow \left(\frac{1}{\cos \theta }\right)\mathrm{\nabla }\times {{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{a^2}{a^2+b^2}]{\zeta }_3\tan \theta +[\frac{a^2}{a^2+c^2}\left]{\zeta }_2\right\}+{\hat{\mathit{k}}}^{\prime }\left\{\right[\frac{b^2}{a^2+b^2}]{\zeta }_3+[\frac{a^2}{a^2+b^2}]{\zeta }_3-[\frac{c^2}{a^2+c^2}]{\zeta }_2\tan \theta -[\frac{a^2}{a^2+c^2}]{\zeta }_2\tan \theta \}$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }\left[\frac{a^2}{a^2+b^2}\right]\{{\zeta }_3\tan \theta +\frac{b^2}{c^2}[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\left]{\zeta }_2\right\}+{\hat{\mathit{k}}}^{\prime }\{{\zeta }_3-{\zeta }_2\tan \theta \}$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }\left[\frac{a^2}{a^2+b^2}\right][1-\frac{b^2}{c^2}]{\zeta }_3\tan \theta +{\hat{\mathit{k}}}^{\prime }\{{\zeta }_3-{\zeta }_2\tan \theta \}$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }\left[\frac{a^2(c^2-b^2)}{c^2(a^2+b^2)}\right]{\zeta }_3\tan \theta +{\hat{\mathit{k}}}^{\prime }\{{\zeta }_3-{\zeta }_2\tan \theta \}$
	$=$	$-{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{a^2(c^2-b^2)}{b^2(a^2+c^2)}\right]{\zeta }_2+{\hat{\mathit{k}}}^{\prime }\{{\zeta }_3-{\zeta }_2\tan \theta \}.$

---

Can we obtain this result by starting from the original, rotating body frame coordinate expression, then transforming the coordinates ?

$\mathrm{\nabla }\times {\mathit{u}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	$\hat{\mathit{ȷ}}{\zeta }_2+\hat{\mathit{k}}{\zeta }_3$
	$=$	$[{\hat{\mathit{ȷ}}}^{\prime }\cos \theta -{\hat{\mathit{k}}}^{\prime }\sin \theta ]{\zeta }_2+[{\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathit{k}}}^{\prime }\cos \theta ]{\zeta }_3$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }[{\zeta }_2\cos \theta +{\zeta }_3\sin \theta ]+{\hat{\mathit{k}}}^{\prime }[{\zeta }_3\cos \theta -{\zeta }_2\sin \theta ]$
$\Rightarrow \left(\frac{1}{\cos \theta }\right)\mathrm{\nabla }\times {\mathit{u}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ȷ}}}^{\prime }[{\zeta }_2+{\zeta }_3\tan \theta ]+{\hat{\mathit{k}}}^{\prime }[{\zeta }_3-{\zeta }_2\tan \theta ]$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }[1+(\frac{{\zeta }_3}{{\zeta }_2})\tan \theta ]{\zeta }_2+{\hat{\mathit{k}}}^{\prime }[{\zeta }_3-{\zeta }_2\tan \theta ]$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }\{1-[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\left]\right\}{\zeta }_2+{\hat{\mathit{k}}}^{\prime }[{\zeta }_3-{\zeta }_2\tan \theta ]$
	$=$	${\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{b^2(a^2+c^2)-c^2(a^2+b^2)}{b^2(a^2+c^2)}\left]\right\}{\zeta }_2+{\hat{\mathit{k}}}^{\prime }[{\zeta }_3-{\zeta }_2\tan \theta ]$
	$=$	$-{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{a^2(c^2-b^2)}{b^2(a^2+c^2)}\right]{\zeta }_2+{\hat{\mathit{k}}}^{\prime }[{\zeta }_3-{\zeta }_2\tan \theta ].$

Q.E.D.

---

Let's see if we can rewrite this expression in a more physically insightful way.

$[1+{\tan }^2\theta {]}^{1/2}\mathrm{\nabla }\times {\mathit{u}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

$=$

${\hat{\mathit{ȷ}}}^{\prime }[{\zeta }_2+{\zeta }_3\tan \theta ]+{\hat{\mathit{k}}}^{\prime }[{\zeta }_3-{\zeta }_2\tan \theta ],$

where,

$\tan \theta$

$=$

$-\left[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\right]\frac{{\zeta }_2}{{\zeta }_3}.$

Summary Vorticity Expressions

1. Written in terms of the (unprimed) body-frame coordinates,

   $\mathrm{\nabla }\times {\mathit{u}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

   $=$

   $\hat{\mathit{ȷ}}{\zeta }_2+\hat{\mathit{k}}{\zeta }_3.$

2. If we view the fluid motion from a (double-primed) frame that is tilted with respect to the (unprimed) body frame by the angle, $\chi$, such that,

   $\tan \chi$

   $=$

   $-\frac{{\zeta }_2}{{\zeta }_3},$

   then ${\hat{\mathit{k}}}^{″}$ will align with the vorticity vector and the vorticity vector will have only one component, namely,

   $\mathrm{\nabla }\times {{\mathit{u}}^{″}}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

   $=$

   ${\hat{\mathit{k}}}^{″}({\zeta }_2^2+{\zeta }_3^2{)}^{1/2}.$

3. If we view the fluid motion from a (single-primed) frame that is tilted with respect to the (unprimed) body frame by an angle, $\theta$, such that the motion of Lagrangian fluid elements is everywhere parallel to the x'-y' plane — that is, such that there is no Lagrangian fluid motion in the ${\hat{\mathit{k}}}^{\prime }$ direction — we find,

   $\tan \theta$

   $=$

   $-\frac{\beta {\mathrm{\Omega }}_2}{\gamma {\mathrm{\Omega }}_3}=-\left[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\right]\frac{{\zeta }_2}{{\zeta }_3},$

   and,

   $\mathrm{\nabla }\times {{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

   $=$

   ${\hat{\mathit{ȷ}}}^{\prime }\stackrel{\mathrm{d}\mathrm{u}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{r}}{\overbrace{[{\zeta }_2\cos \theta +{\zeta }_3\sin \theta ]}}+{\hat{\mathit{k}}}^{\prime }\underset{{\zeta }_L}{\underbrace{[{\zeta }_3\cos \theta -{\zeta }_2\sin \theta ]}}.$

4. From below, the contribution to the vorticity that is provided by the Lagrangian orbital-element-based description of the motion of the fluid is,

   ${\zeta }_{\mathrm{L}}$

   $\equiv$

   $\{\frac{\partial {\dot{y}}^{\prime }}{\partial x^{\prime }}-\frac{\partial {\dot{x}}^{\prime }}{\partial y^{\prime }}\}=\left[\right(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}})+(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left)\right]\dot{\phi }.$

   1. Adopting the parameter (Model001 evaluation in parentheses),

      $\mathrm{\Lambda }$

      $\equiv$

      $\left[\frac{a^2}{a^2+b^2}\right]{\zeta }_3\cos \theta -\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_2\sin \theta =-1.332892,$

      we have found that,

      $\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}$

      $=$

      $\left\{\mathrm{\Lambda }\right[\frac{a^2+b^2}{b^2}]\frac{\cos \theta }{{\zeta }_3}{\}}^{1/2}=1.025854,$

      and,

      $\dot{\phi }$

      $=$

      $\left\{\mathrm{\Lambda }\right[\frac{b^2}{a^2+b^2}]\frac{{\zeta }_3}{\cos \theta }{\}}^{1/2}=1.299300,$

      which implies,

      ${\zeta }_L{|}_{\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{0}\mathrm{0}\mathrm{1}}$

      $=$

      $2.599446.$

   2. Alternatively, we have found that,

      $\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}$

      $=$

      $\frac{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{bc}=1.025854,$

      and,

      $\dot{\phi }$

      $=$

      $\frac{{\zeta }_3}{\cos \theta }\left[\frac{abc(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{c^2(a^2+b^2)}\right]=-1.299300,$

      which implies,

      ${\zeta }_L{|}_{\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{0}\mathrm{0}\mathrm{1}}$

      $=$

      $-2.599446.$

   3. In step #3, immediately above, we have determined that the ${\hat{\mathit{k}}}^{\prime }$ component of the fluid vorticity is given by the expression,

      ${\zeta }_L$

      $=$

      $({\zeta }_3\cos \theta -{\zeta }_2\sin \theta )=-2.599446.$

It appears as though we have separately derived three expressions for the quantity, ${\zeta }_L$. It would be great if we could demonstrate analytically that the three expressions are, indeed, identical. Keep in mind that the definition of $\tan \theta$ establishes the relation, $b^2(a^2+c^2){\zeta }_3\sin \theta$ $=$ $-c^2(a^2+b^2){\zeta }_2\cos \theta$ $\Rightarrow \frac{{\zeta }_3}{c^2(a^2+b^2)\cos \theta }$ $=$ $-\frac{{\zeta }_2}{b^2(a^2+c^2)\sin \theta }$ Let, $\mathrm{{\rm Y}}$ $\equiv$ $(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}.$ Then, ${\zeta }_{\mathrm{L}}$ $=$ $\left[\right(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}})+(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left)\right]\dot{\phi }$   $=$ $[\frac{a\mathrm{{\rm Y}}}{bc}+\frac{bc}{a\mathrm{{\rm Y}}}]\frac{{\zeta }_3}{\cos \theta }\left[\frac{abc\mathrm{{\rm Y}}}{c^2(a^2+b^2)}\right]$   $=$ $\frac{{\zeta }_3}{\cos \theta }\left\{\right[\frac{a\mathrm{{\rm Y}}}{bc}\left]\right[\frac{abc\mathrm{{\rm Y}}}{c^2(a^2+b^2)}]+[\frac{bc}{a\mathrm{{\rm Y}}}\left]\right[\frac{abc\mathrm{{\rm Y}}}{c^2(a^2+b^2)}\left]\right\}$   $=$ $\frac{b^2{\zeta }_3}{(a^2+b^2)\cos \theta }\left\{\right[\frac{a^2{\mathrm{{\rm Y}}}^2}{b^2{c}^2}]+1\}$   $=$ $\frac{{\zeta }_3}{c^2(a^2+b^2)\cos \theta }\left\{\right[a^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )]+b^2{c}^2\}$   $=$ $\frac{{\zeta }_3}{c^2(a^2+b^2)\cos \theta }\{a^2{c}^2{\cos }^2\theta +a^2{b}^2{\sin }^2\theta +b^2{c}^2({\sin }^2\theta +{\cos }^2\theta )\}$   $=$ $\frac{{\zeta }_3}{c^2(a^2+b^2)\cos \theta }\{c^2(a^2+b^2){\cos }^2\theta \}+\frac{{\zeta }_3}{c^2(a^2+b^2)\cos \theta }\{b^2(a^2+c^2){\sin }^2\theta \}$   $=$ ${\zeta }_3\cos \theta -{\zeta }_2\sin \theta .$ Q.E.D. Alternatively, pulling from the expressions that have been derived in terms of the parameter, $\mathrm{\Lambda }$, we find, ${\zeta }_{\mathrm{L}}$ $=$ $\left[\right(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}})+(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left)\right]\dot{\phi }$   $=$ $\left\{\mathrm{\Lambda }\right[\frac{a^2+b^2}{b^2}\left]\frac{\cos \theta }{{\zeta }_3}{\}}^{1/2}\right\{\mathrm{\Lambda }\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }{\}}^{1/2}+\left\{{\mathrm{\Lambda }}^{-1}\right[\frac{b^2}{a^2+b^2}\left]\frac{{\zeta }_3}{\cos \theta }{\}}^{1/2}\right\{\mathrm{\Lambda }\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }{\}}^{1/2}$   $=$ $\mathrm{\Lambda }+\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }$   $=$ $\left[\frac{a^2}{a^2+b^2}\right]{\zeta }_3\cos \theta -\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_2\sin \theta +\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }\{{\sin }^{}\theta +{\cos }^{}\theta \}$   $=$ ${\zeta }_3\cos \theta -\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_2\sin \theta +\left[b^2{c}^2\right]\frac{{\zeta }_3}{c^2(a^2+b^2)\cos \theta }\left\{{\sin }^{}\theta \right\}$   $=$ ${\zeta }_3\cos \theta -\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_2\sin \theta -\left[b^2{c}^2\right]\frac{{\zeta }_2}{b^2(a^2+c^2)\sin \theta }\left\{{\sin }^{}\theta \right\}$   $=$ ${\zeta }_3\cos \theta -{\zeta }_2\sin \theta .$ Q.E.D.

Lagrangian Fluid Trajectories

Off-Center Ellipse

The yellow dots in Figures 2a and 2b trace three different, nearly circular, closed curves. These curves each show what results from the intersection of the surface of the triaxial ellipsoid and a plane that is tilted with respect to the x = x' axis by the specially chosen angle, $\theta$; the different curves result from different choices of the intersection point, $z_0$. Several additional such curves are displayed in Figure 2c. Each of these curves necessarily also identifies the trajectory that is followed by a fluid element that sits on the surface of the ellipsoid.

We have determined that the $y^{\prime }(x^{\prime })$ function that defines each closed curve is describable analytically by the expression,

$[\frac{y^{\prime }-y{\text{'}}_0}{y{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2$

$=$

$1-(\frac{x^{\prime }}{x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2,$

where (see independent derivations with identical results from ChallengesPt2 and ChallengesPt6),

$x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$	$=$	$a[1-\frac{z_0^2{\cos }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{]}^{1/2}$
	$=$	$a[\frac{(c^2-z_0^2){\cos }^2\theta +b^2{\sin }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{]}^{1/2},$
$y{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$	$=$	$bc[(c^2{\cos }^2\theta +b^2{\sin }^2\theta )-z_0^2{\cos }^2\theta {]}^{1/2}(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{-1}$
	$=$	$bc[\frac{(c^2-z_0^2){\cos }^2\theta +b^2{\sin }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^2}{]}^{1/2},$
$y{\text{'}}_0$	$=$	$-\frac{z_0{b}^2\sin \theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}.$

This is the equation that describes a closed ellipse with semi-axes, $(x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}},y{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}})$, that is offset from the z'-axis along the y'-axis by a distance, $y{\text{'}}_0$. Notice that the degree of flattening,

$[\frac{x^{\prime }}{y^{\prime }}{]}_{\mathrm{m}\mathrm{a}\mathrm{x}}$

$=$

$\frac{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{bc},$

is independent of $z_0$; that is to say, the degree of flattening of all of the elliptical trajectories is identical! Notice, as well, that the y-offset, $y{\text{'}}_0$, is linearly proportional to $z_0$.

In a separate discussion, we have demonstrated that the compact version of the tilted flow-field is everywhere orthogonal to the elliptical trajectory whose analytic definition is given by the off-set ellipse equation.

Associated Lagrangian Velocities

Let's presume that, as a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,

$x^{\prime }$	$=$	$x_{\mathrm{m}\mathrm{a}\mathrm{x}}\cos (\dot{\phi }t)$	and,	$y^{\prime }-y_0$	$=$	$y_{\mathrm{m}\mathrm{a}\mathrm{x}}\sin (\dot{\phi }t),$
${\dot{x}}^{\prime }$	$=$	$-x_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }\cdot \sin (\dot{\phi }t)=(y_0-y^{\prime })\left[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }$	and,	${\dot{y}}^{\prime }$	$=$	$y_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }\cdot \cos (\dot{\phi }t)=x^{\prime }\left[\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }.$

If this is the correct description of the Lagrangian motion in a $z^{\prime }=0$ plane of motion, then the velocity components, ${\dot{x}}^{\prime }$ and ${\dot{y}}^{\prime }$, must match the respective components of the Riemann flow-field, namely,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}{|}_{z^{\prime }=0}$

$=$

${\hat{\mathit{ı}}}^{\prime }\left\{\right[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}+{\hat{\mathit{ı}}}^{\prime }\{{\xcancel{z^{\prime }(c^2-b^2)\tan \theta }}^0-y^{\prime }[c^2+b^2{\tan }^2\theta ]\}\frac{{\zeta }_3\cos \theta }{c^2}\left[\frac{a^2}{a^2+b^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3{x}^{\prime }}{\cos \theta }.$

First, let's compare the ${\hat{\mathit{ȷ}}}^{\prime }$ components.

$x^{\prime }[\frac{y^{\prime }}{x^{\prime }}{]}_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }$	$\leftrightarrow$	$x^{\prime }\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }$
$\Rightarrow \dot{\phi }$	$=$	$\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }[\frac{x^{\prime }}{y^{\prime }}{]}_{\mathrm{m}\mathrm{a}\mathrm{x}}$
	$=$	$\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }\left[\frac{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{bc}\right]$
	$=$	$\frac{{\zeta }_3}{\cos \theta }\left[\frac{abc(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{c^2(a^2+b^2)}\right].$

Now let's compare the ${\hat{\mathit{ı}}}^{\prime }$ components.

$(y_0-y^{\prime })[\frac{x^{\prime }}{y^{\prime }}{]}_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }$	$\leftrightarrow$	$\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_2{z}_0-y^{\prime }[c^2+b^2{\tan }^2\theta ]\frac{{\zeta }_3\cos \theta }{c^2}\left[\frac{a^2}{a^2+b^2}\right]$
$\Rightarrow (y_0-y^{\prime })\dot{\phi }$	$=$	$\left\{\right[\frac{a^2}{a^2+c^2}]{\zeta }_2{z}_0-y^{\prime }[c^2+b^2{\tan }^2\theta ]\frac{{\zeta }_3\cos \theta }{c^2}[\frac{a^2}{a^2+b^2}\left]\right\}[\frac{y^{\prime }}{x^{\prime }}{]}_{\mathrm{m}\mathrm{a}\mathrm{x}}$
	$=$	$\left\{\right[\frac{a^2}{a^2+c^2}]{\zeta }_2{z}_0-y^{\prime }[c^2+b^2{\tan }^2\theta \left]\frac{{\zeta }_3\cos \theta }{c^2}\right[\frac{a^2}{a^2+b^2}\left]\right\}\left[\frac{bc}{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}\right].$

Inserting the just-derived expression for $\dot{\phi }$ into this last expression gives,

$(y_0-y^{\prime })$	$=$	$\left\{\right[\frac{a^2}{a^2+c^2}]{\zeta }_2{z}_0-y^{\prime }[c^2+b^2{\tan }^2\theta \left]\frac{{\zeta }_3\cos \theta }{c^2}\right[\frac{a^2}{a^2+b^2}\left]\right\}\left[\frac{bc}{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}\right]\left[\frac{a^2+b^2}{b^2}\right]\frac{\cos \theta }{{\zeta }_3}\left[\frac{bc}{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}\right]$
	$=$	$\left\{\right[\frac{a^2}{a^2+c^2}]{\zeta }_2{z}_0-y^{\prime }[c^2+b^2{\tan }^2\theta \left]\frac{{\zeta }_3\cos \theta }{c^2}\right[\frac{a^2}{a^2+b^2}\left]\right\}\frac{\cos \theta }{{\zeta }_3}\left[\frac{c^2(a^2+b^2)}{a^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}\right]$
	$=$	$\left\{\right[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}\frac{\cos \theta }{{\zeta }_3}\left[\frac{c^2(a^2+b^2)}{a^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}\right]+\{-y^{\prime }[c^2+b^2{\tan }^2\theta \left]\frac{{\zeta }_3\cos \theta }{c^2}\right[\frac{a^2}{a^2+b^2}\left]\right\}\frac{\cos \theta }{{\zeta }_3}\left[\frac{c^2(a^2+b^2)}{a^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}\right]$
	$=$	$\left\{\right[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\left]\frac{{\zeta }_2}{{\zeta }_3}\right\}\left[\frac{b^2{z}_0\cos \theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}\right]-y^{\prime }.$

But,

$\tan \theta$

$=$

$-\left[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\right]\frac{{\zeta }_2}{{\zeta }_3}.$

Hence,

$(y_0-y^{\prime })$	$=$	$\left[\frac{-b^2{z}_0\sin \theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}\right]-y^{\prime }.$
$\Rightarrow y_0$	$=$	$\left[\frac{-b^2{z}_0\sin \theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}\right].$

SUCCESS !!!

Vorticity Implied by Lagrangian Fluid Motions

As we have stated above, the motion of fluid elements in the primed (preferred tilted-plane) coordinate system is given by the pair of expressions,

${u_x}^{\prime }={\dot{x}}^{\prime }$

$=$

$(y_0-y^{\prime })\left[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }$

and,

${u_y}^{\prime }={\dot{y}}^{\prime }$

$=$

$x^{\prime }\left[\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }.$

So, the contribution to the local vorticity that is provided by orbital motion of individual Lagrangian fluid elements is,

${\zeta }_{\mathrm{L}}$	$=$	$\{\frac{\partial u{\text{'}}_y}{\partial x^{\prime }}-\frac{\partial u{\text{'}}_x}{\partial y^{\prime }}\}$
	$=$	$\left[\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }+\left[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }$
	$=$	$\left[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2+y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }.$

That is,

${\zeta }_{\mathrm{L}}$	$=$	$\{\frac{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{bc}+\frac{bc}{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}\}\frac{{\zeta }_3}{\cos \theta }\left[\frac{abc(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{c^2(a^2+b^2)}\right]$
	$=$	$\left\{\frac{a^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )+b^2{c}^2}{c^2(a^2+b^2)}\right\}\frac{{\zeta }_3}{\cos \theta }$
	$=$	$\left\{\frac{a^2(c^2-b^2){\cos }^2\theta +b^2(a^2+c^2)}{c^2(a^2+b^2)}\right\}\frac{{\zeta }_3}{\cos \theta }$
	$=$	$\left\{\frac{a^2(c^2-b^2)}{c^2(a^2+b^2)}\right\}{\zeta }_3\cos \theta +\left\{\frac{b^2(a^2+c^2)}{c^2(a^2+b^2)}\right\}\frac{{\zeta }_3}{\cos \theta }$

But,

$\tan \theta$	$=$	$-\left[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\right]\frac{{\zeta }_2}{{\zeta }_3}$
$\Rightarrow \left[\frac{b^2(a^2+c^2)}{c^2(a^2+b^2)}\right]\frac{{\zeta }_3}{\cos \theta }$	$=$	$-\frac{{\zeta }_2}{\sin \theta },$

in which case,

${\zeta }_{\mathrm{L}}$	$=$	$\left\{\frac{a^2(c^2-b^2)}{c^2(a^2+b^2)}\right\}{\zeta }_3\cos \theta -\frac{{\zeta }_2}{\sin \theta }$
${\zeta }_{\mathrm{L}}$	$=$	$\left\{\frac{a^2(c^2-b^2)}{c^2(a^2+b^2)}\right\}{\zeta }_3\cos \theta -\frac{{\zeta }_2}{\sin \theta }$

Summary & Example

Model001

This particular set of seven key parameters has been drawn from [EFE] Chapter 7, Table XIII (p. 170). The tabular layout presented here, also appears in a related discussion labeled, Challenges Pt. 2.

Model001:   $(\frac{a_2}{a_1},\frac{a_3}{a_1})=(1.2500,0.4703)$
$A_1$		$A_2$		$A_3$
0.48955940032702523984		0.36486593343389634429		1.1455746662390784159
Direct
${\beta }_{+}$	${\gamma }_{+}$	${\mathrm{\Omega }}_2=\hat{\mathit{ȷ}}\cdot {\overrightarrow{\mathrm{\Omega }}}_f$	${\mathrm{\Omega }}_3=\hat{\mathit{k}}\cdot {\overrightarrow{\mathrm{\Omega }}}_f$	${\zeta }_2=\hat{\mathit{ȷ}}\cdot \overrightarrow{\zeta }$	${\zeta }_3=\hat{\mathit{k}}\cdot \overrightarrow{\zeta }$
1.1343563893093	1.8050153443093	0.3639465285418	0.6633461900921	-2.2793843997547	-1.9636540847967
$\tan \theta$	$\theta$ (deg.)	$|z_0{|}_{\mathrm{m}\mathrm{a}\mathrm{x}}$	$\frac{y_0}{z_0}$	$[\frac{x^{\prime }}{y^{\prime }}{]}_{\mathrm{m}\mathrm{a}\mathrm{x}}$	$\dot{\phi }$
-0.3447989745608	-19.02414	0.6379200460018	-1.4003818611184	1.0258604183520	-1.2992789284526
				${\hat{\mathit{ȷ}}}^{\prime }\cdot \overrightarrow{\zeta }$	${\zeta }_L={\hat{\mathit{k}}}^{\prime }\cdot \overrightarrow{\zeta }$
				-1.5148019600561	-2.5994048604237
Adjoint
${\beta }_{-}$	${\gamma }_{-}$	${\mathrm{\Omega }}_2^{†}=\hat{\mathit{ȷ}}\cdot {\overrightarrow{\mathrm{\Omega }}}_f^{†}$	${\mathrm{\Omega }}_3^{†}=\hat{\mathit{k}}\cdot {\overrightarrow{\mathrm{\Omega }}}_f^{†}$	${\zeta }_2^{†}=\hat{\mathit{ȷ}}\cdot {\overrightarrow{\zeta }}^{†}$	${\zeta }_3^{†}=\hat{\mathit{k}}\cdot {\overrightarrow{\zeta }}^{†}$
0.1949846556907	0.8656436106907	0.8778334467750	0.9578800413643	-0.9450244149966	-1.3598596896888
$\tan \theta$	$\theta$ (deg.)	$|z_0{|}_{\mathrm{m}\mathrm{a}\mathrm{x}}$	$\frac{y_0}{z_0}$	$[\frac{x^{\prime }}{y^{\prime }}{]}_{\mathrm{m}\mathrm{a}\mathrm{x}}$	$\dot{\phi }$
-0.2064250069478	-11.663458271	0.5364347308466	-1.1444841125518	0.8936566385511	-0.7566275461198
				${\hat{\mathit{ȷ}}}^{\prime }\cdot {\overrightarrow{\zeta }}^{†}$	${\zeta }_L^{†}={\hat{\mathit{k}}}^{\prime }\cdot {\overrightarrow{\zeta }}^{†}$
				-0.6505985480434	-1.5228299477827

As a consequence, the time-dependent x'-y' coordinate positions of individual Lagrangian fluid elements is precisely describe by the expressions,

$x^{\prime }$

$=$

$x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\cos (\dot{\phi }t)$

and,

$y^{\prime }-y_0$

$=$

$y{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\sin (\dot{\phi }t),$

and — see an accompanying discussion (alternatively, ChallengesPt6) for details — the values of these additional key parameters are …

					Example Values
$\tan \theta$	$=$	$-\frac{{\zeta }_2}{{\zeta }_3}\left[\frac{a^2+b^2}{a^2+c^2}\right]\frac{c^2}{b^2}=-0.344793$			$\theta =$	$-19.0238^{\circ }$
$z_0^2$	$\le$	$c^2+b^2{\tan }^2\theta$			$z_0^2\le$	$0.40694$
$\frac{y_0}{z_0}$	$=$	$-\frac{b^2\sin \theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}$			$\frac{y_0}{z_0}=$	$+1.400377$
For $1\ge h>0$,      $\left|\frac{x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{a}\right|$	$=$	$[\frac{(c^2-z_0^2){\cos }^2\theta +b^2{\sin }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{]}^{1/2}\cdot h$			$\left|\frac{x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{a}\right|$	varies with choice of $z_0^2$
$\frac{x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$	$=$	$\frac{a(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{bc}$			$\frac{x{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}=$	$+1.025854$
$\dot{\phi }$	$=$	$\frac{{\zeta }_3}{\cos \theta }\left[\frac{abc(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{c^2(a^2+b^2)}\right]$			$\dot{\phi }=$	$-1.2993$

Example Sequences

Let's plot sequences in which …

• $f\equiv ({\zeta }_2^2+{\zeta }_3^2{)}^{1/2}/({\mathrm{\Omega }}_2^2+{\mathrm{\Omega }}_3^2{)}^{1/2}$ is constant; this is the analog of $f=\zeta /{\mathrm{\Omega }}_f$ in Riemann S-type Ellipsoids.
• ${\zeta }_L/({\zeta }_2^2+{\zeta }_3^2{)}^{1/2}$ is constant.
• $(x^{\prime }/y^{\prime }{)}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is constant.

See Also

• Description of Riemann Type I Ellipsoids (best)
• Description of Riemann Type I Ellipsoids (older introduction)
• Riemann Type 1 Ellipsoids (oldest introduction)
• Construction Challenges (Pt. 1)
• Construction Challenges (Pt. 2)
• Construction Challenges (Pt. 3)
• Construction Challenges (Pt. 4)
• Construction Challenges (Pt. 5)
• Construction Challenges (Pt. 6)

• Related discussions of models viewed from a rotating reference frame:
  • PGE
  • NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.