Appendix/FormatRecommendations
Format Recommendations
Equations
Simplest Form
Example extracted from Wiki chapter titled: Dyson (1893)
|
|
|
|
Raw text used to generate this simple equation:
<!-- (BEGIN) Raw Text Providing a Template for Mathematical Expression in its Simplest Form-->
<table border="0" cellpadding="5" align="center">
<tr>
<td align="right">
<math>\biggl[ \frac{\pi}{GM}\biggr] \Phi_\mathrm{TR}</math>
</td>
<td align="center">
<math>=</math>
</td>
<td align="left">
<math>- \frac{2K(k)}{R_1} \, ,</math>
</td>
</tr>
</table>
<!-- (END) Raw Text Providing a Template for Mathematical Expression in its Simplest Form-->
With Title and References
Example extracted from Wiki chapter titled: Ostriker (1964)
|
Scalar Gravitational Potential |
||
|
|
|
|
|
[BT87], p. 31, Eq. (2-3) |
||
Raw text used to generate this expression ensemble:
<!-- (BEGIN) Raw Text Providing a Template for Mathematical Expression with Title and References-->
<div align="center" id="GravitationalPotential">
<table border="0" cellpadding="5" align="center">
<tr>
<td align="center" colspan="3">
<font color="#770000">'''Scalar Gravitational Potential'''</font>
</td>
</tr>
<tr>
<td align="right">
<math>\Phi(\vec{x})</math>
</td>
<td align="center">
<math>\equiv</math>
</td>
<td align="left">
<math> -G \iiint \frac{\rho(\vec{x}^{~'})}{|\vec{x}^{~'} - \vec{x}|} d^3x^' \, .</math>
</td>
</tr>
<tr>
<td align="center" colspan="3">
[<b>[[Appendix/References#BT87|<font color="red">BT87</font>]]</b>], p. 31, Eq. (2-3)<br />
[<b>[[Appendix/References#EFE|<font color="red">EFE</font>]]</b>], §10, p. 17, Eq. (11)<br />
[<b>[[Appendix/References#T78|<font color="red">T78</font>]]</b>], §4.2, p. 77, Eq. (12)
</td>
</tr>
</table>
</div>
<!-- (END) Raw Text Providing a Template for Mathematical Expression with Title and References-->
Multiple Lines
Example extracted from Wiki chapter titled: Dyson (1893)
|
|
|
|
|
|
|
|
|
|
|
|
Raw text used to generate this multi-line expression:
<!-- (BEGIN) Raw Text Providing a Template for Multiline Mathematical Expression -->
<table border="0" cellpadding="5" align="center">
<tr>
<td align="right">
<math>\biggl[ \frac{\pi}{GM}\biggr] \Phi_\mathrm{TR}</math>
</td>
<td align="center">
<math>=</math>
</td>
<td align="left">
<math>- \frac{2}{R_1} \biggl[(1+k_1)K(k_1) \biggr] </math>
</td>
</tr>
<tr>
<td align="right">
</td>
<td align="center">
<math>=</math>
</td>
<td align="left">
<math>- \frac{2K(\mu)}{R_1} \biggl[1+\frac{R_1-R}{R_1+R} \biggr] </math>
</td>
</tr>
<tr>
<td align="right">
</td>
<td align="center">
<math>=</math>
</td>
<td align="left">
<math>- \frac{4K(\mu)}{R_1+R} \, .</math>
</td>
</tr>
</table>
<!-- (END) Raw Text Providing a Template for Multiline Mathematical Expression -->
References
Books
[BLRY07], p. 14, Eq. (1.60)
[<b>[[Appendix/References#BLRY07|<font color="red">BLRY07</font>]]</b>], p. 14, Eq. (1.60)
Journal-Article Templates
Example extracted from reference BAC84
📚 J. R. Bond, W. D. Arnett, & B. J. Carr (1984, ApJ, Vol. 280, pp. 825 - 847)
📚 Bond, Arnett, & Carr (1984)
BAC84
The Evolution and Fate of Very Massive Objects
The Astrophysical Journal, Vol. 280, May 15, pp. 825 - 847
| Acknowledgements (p. 844): "We thank Willy Fowler, Lee Lindblom, Wolfgang Ober, Bob Wagoner, and Stan Woosley for useful discussions. In particular, Stan Woosley often emphasized the many ways rotation could transform simplicity into complexity. This research was supported by grants NSF AST-80-22876 at Chicago, NSF AST 79-23243 at Berkeley, and NSF PHY 81-19387 at Stanford, and by the SERC at Cambridge." |
|
Click to list chapter(s) on this wiki site that either … cite or display an image/figure/table from this article. |
<!-- (BEGIN) Raw Text Pointing to Four "Template" References -->
{{ BAC84full }}<br />
{{ BAC84 }}<br />
{{ BAC84hereafter }}<br />
<div align="center">{{ BAC84figure }}</div>
<div id="BAC84acknowledgement">
<table border="0" align="center" width="80%">
<tr><td align="left">Acknowledgements (p. 844):<br /><font color="darkgreen">"We thank Willy Fowler, Lee Lindblom, Wolfgang Ober, Bob Wagoner, and Stan Woosley for useful discussions. In particular, Stan Woosley often emphasized the many ways rotation could transform simplicity into complexity. This research was supported by grants NSF [https://www.nsf.gov/awardsearch/simpleSearchResult?queryText=8022876 AST-80-22876] at Chicago, NSF [https://www.nsf.gov/awardsearch/simpleSearchResult?queryText=7923243 AST 79-23243] at Berkeley, and NSF PHY 81-19387 at Stanford, and by the [https://en.wikipedia.org/wiki/Science_and_Engineering_Research_Council SERC] at Cambridge."</font>
</td></tr>
<tr><td align="left">
Click to list chapter(s) on this wiki site that either … <b>[[Special:WhatLinksHere/Template:BAC84full|cite]]</b> or <b>[[Special:WhatLinksHere/Template:BAC84figure|display an image/figure/table from]]</b> this article.
</td></tr>
</table>
</div>
<!-- (END) Raw Text Pointing to Four "Template" References -->
Template: BAC84full
[[Appendix/References#BAC84|📚 ]][https://ui.adsabs.harvard.edu/abs/1984ApJ...280..825B/abstract J. R. Bond, W. D. Arnett, & B. J. Carr (1984, ApJ, Vol. 280, pp. 825 - 847)]
Template: BAC84
[[Appendix/References#BAC84|📚 ]][https://ui.adsabs.harvard.edu/abs/1984ApJ...280..825B/abstract Bond, Arnett, & Carr (1984)]
Template: BAC84hereafter
[[Appendix/References#BAC84|BAC84]]
Template: BAC84figure
[https://ui.adsabs.harvard.edu/abs/1984ApJ...280..825B/abstract J. R. Bond, W. D. Arnett, & B. J. Carr (1984)]<br />''The Evolution and Fate of Very Massive Objects''<br />The Astrophysical Journal, Vol. 280, May 15, pp. 825 - 847
Darkgreen Quotation Inset
Example extracted from Wiki chapter titled: Onset of Bar-mode Instability …
|
"… the onset of instability is not very sensitive to the compressibility or angular momentum distribution of the polytrope when the models are parameterized by T/|W| — [in particular, the m = 2 barmode becomes unstable at T/|W| ∼ 0.26 - 0.28. ] The polytrope eigenfunctions are … qualitatively different from the Maclaurin eigenfunctions in one respect: they develop strong spiral arms. The spiral arms are stronger for more compressible polytropes and for polytropes whose angular momentum distributions deviate significantly from those of the Maclaurin spheroids." |
|
— Drawn from Toman, Imamura, Pickett & Durisen (1998), ApJ, 497, 370 |
Raw text used to generate this example quotation inset:
<!-- (BEGIN) Raw Text Providing a Template for Darkgreen Quotation Inset--> <table border="0" cellpadding="3" align="center" width="80%"> <tr><td align="left"> <font color="darkgreen"> "… the onset of instability is not very sensitive to the compressibility or angular momentum distribution of the polytrope when the models are parameterized by T/|W|</font> — [in particular, the m = 2 barmode becomes unstable at T/|W| ∼ 0.26 - 0.28. ] <font color="darkgreen">The polytrope eigenfunctions are … qualitatively different from the Maclaurin eigenfunctions in one respect: they develop strong spiral arms. The spiral arms are stronger for more compressible polytropes and for polytropes whose angular momentum distributions deviate significantly from those of the Maclaurin spheroids." </font> </td></tr> <tr><td align="right"> — Drawn from [https://ui.adsabs.harvard.edu/abs/1998ApJ...497..370T/abstract Toman, Imamura, Pickett & Durisen (1998)], ApJ, 497, 370 </td></tr></table> <!-- (END) Raw Text Providing a Template for Darkgreen Quotation Inset-->
Comment Balloon (Pink)
Example extracted from Wiki chapter titled: Maclaurin Spheroids

We know from our separate discussion of supplemental, barotropic equations of state that, for a uniform-density,
polytropic configuration, the pressure is related to the enthalpy via the expression,
. Hence, we conclude that,
|
|
|
|
|
[T78], §4.5, p. 86, Eq. (51) |
||
Raw text used to generate this illustration of the pink comment balloon:
<!-- (BEGIN) raw text illustrating pink comment balloon -->
[[File:CommentButton02.png|right|100px|Comment by J. E. Tohline: In Tassoul (1978), the leading coefficient in the expression for the pressure — and, hence, the central pressure — is too large by a factor of 2.]]We know from our [[SR#Barotropic_Structure|separate discussion of supplemental, barotropic equations of state]] that, for a uniform-density, <math>~n = 0</math> polytropic configuration, the pressure is related to the enthalpy via the expression, <math>~P = H\rho</math>. Hence, we conclude that,
<table align="center" border="0" cellpadding="5">
<tr>
<td align="right">
<math>
P(\varpi,z)
</math>
</td>
<td align="center">
<math>
=
</math>
</td>
<td align="left">
<math>
\pi G \rho^2 a_1^2 A_3 (1-e^2)\biggl[1 - \biggl( \frac{\varpi}{a_1} \biggr)^2 - \biggl( \frac{z}{a_3} \biggr)^2
\biggr]
</math>
</td>
</tr>
<tr>
<td align="center" colspan="3">
[<b>[[Appendix/References#T78|<font color="red">T78</font>]]</b>], §4.5, p. 86, Eq. (51)<br />
[<b>[[Appendix/References#ST83|<font color="red">ST83</font>]]</b>], §7.3, p. 172, Eqs. (7.3.16) & (7.3.17)
</td>
</tr>
</table>
<!-- (END) raw text illustrating pink comment balloon -->
Wikitable Overflow
Example extracted from Wiki chapter titled: Toroidal Configurations and Related Coordinate Systems
| Example 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Torus Intersection Points | |||||||||
| Intersection #1 (superior sign) | Intersection #2 (inferior sign) | ||||||||
| Degenerate Coordinate Values | |||||||||
| Degenerate Coordinate Values | |||||||||
In order to see how this overflow command works, place your mouse cursor anywhere inside the displayed table, then scroll down/up. Here is the raw text illustrating how to handle "Wikitable Overflow":
<!-- (BEGIN) Raw Text Providing Example of Wikitable Overflow -->
<div id="Example2" style="width: 85%; height: 15em; overflow: auto;">
<table align="center" border="1" cellpadding="5">
<tr><th align="center" colspan="10">Example 2</th></tr>
<tr>
<td align="center" colspan="2" width="25%"><math>~\varpi_t</math></td>
<td align="center" colspan="2" width="25%"><math>~r_t</math></td>
<td align="center" colspan="2" width="25%"><math>~Z_0</math></td>
<td align="center" colspan="2"><math>~a</math></td>
<td align="center" colspan="2"><math>~\Kappa</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~\tfrac{3}{4}</math></td>
<td align="center" colspan="2"><math>~\tfrac{1}{4}</math></td>
<td align="center" colspan="2"><math>~\tfrac{3}{4}</math></td>
<td align="center" colspan="2"><math>~\tfrac{1}{3}</math></td>
<td align="center" colspan="2"><math>~(\tfrac{5}{12})^2</math></td>
</tr>
<tr>
<th colspan="10" align="center">Torus Intersection Points</th>
</tr>
<tr>
<td align="center" colspan="2" rowspan="2"><math>~\xi_1</math></td>
<td align="center" colspan="1" rowspan="2"><math>~\beta</math></td>
<td align="center" colspan="1" rowspan="2"><math>~\ell</math></td>
<td align="center" colspan="3" bgcolor="yellow">Intersection #1 (''superior'' sign)</td>
<td align="center" colspan="3" bgcolor="yellow">Intersection #2 (''inferior'' sign)</td>
</tr>
<tr>
<td align="center"><math>~\xi_2</math>
<td align="center"><math>~\varpi_i</math>
<td align="center"><math>~z_i</math>
<td align="center"><math>~\xi_2</math>
<td align="center"><math>~\varpi_i</math>
<td align="center"><math>~z_i</math>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.1927843</math></td>
<td align="center" colspan="1"><math>~+0.138485</math></td>
<td align="center" colspan="1"><math>~1.000000</math></td>
<td align="center" colspan="1"><math>~0.885198</math></td>
<td align="center" colspan="1"><math>~0.704606</math></td>
<td align="center" colspan="1"><math>~0.245844</math></td>
<td align="center" colspan="3">Degenerate Coordinate Values</td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.176</math></td>
<td align="center" colspan="1"><math>~+0.116568</math></td>
<td align="center" colspan="1"><math>~0.981258</math></td>
<td align="center" colspan="1"><math>~0.922142</math></td>
<td align="center" colspan="1"><math>~0.812595</math></td>
<td align="center" colspan="1"><math>~0.242037</math></td>
<td align="center" colspan="1"><math>~0.841611</math></td>
<td align="center" colspan="1"><math>~0.616896</math></td>
<td align="center" colspan="1"><math>~0.211621</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.160</math></td>
<td align="center" colspan="1"><math>~+0.092267</math></td>
<td align="center" colspan="1"><math>~0.962725</math></td>
<td align="center" colspan="1"><math>~0.933386</math></td>
<td align="center" colspan="1"><math>~0.864726</math></td>
<td align="center" colspan="1"><math>~0.222121</math></td>
<td align="center" colspan="1"><math>~0.824945</math></td>
<td align="center" colspan="1"><math>~0.584858</math></td>
<td align="center" colspan="1"><math>~0.187691</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.144</math></td>
<td align="center" colspan="1"><math>~+0.063705</math></td>
<td align="center" colspan="1"><math>~0.943871</math></td>
<td align="center" colspan="1"><math>~0.940238</math></td>
<td align="center" colspan="1"><math>~0.908969</math></td>
<td align="center" colspan="1"><math>~0.192948</math></td>
<td align="center" colspan="1"><math>~0.813713</math></td>
<td align="center" colspan="1"><math>~0.560766</math></td>
<td align="center" colspan="1"><math>~0.163372</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.127</math></td>
<td align="center" colspan="1"><math>~+0.027202</math></td>
<td align="center" colspan="1"><math>~0.924221</math></td>
<td align="center" colspan="1"><math>~0.944608</math></td>
<td align="center" colspan="1"><math>~0.949856</math></td>
<td align="center" colspan="1"><math>~0.150191</math></td>
<td align="center" colspan="1"><math>~0.806047</math></td>
<td align="center" colspan="1"><math>~0.539788</math></td>
<td align="center" colspan="1"><math>~0.135318</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.111</math></td>
<td align="center" colspan="1"><math>~-0.015045</math></td>
<td align="center" colspan="1"><math>~0.907444</math></td>
<td align="center" colspan="1"><math>~0.946487</math></td>
<td align="center" colspan="1"><math>~0.980806</math></td>
<td align="center" colspan="1"><math>~0.096065</math></td>
<td align="center" colspan="1"><math>~0.802617</math></td>
<td align="center" colspan="1"><math>~0.523232</math></td>
<td align="center" colspan="1"><math>~0.105244</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.094</math></td>
<td align="center" colspan="1"><math>~-0.071947</math></td>
<td align="center" colspan="1"><math>~0.894425</math></td>
<td align="center" colspan="1"><math>~0.945995</math></td>
<td align="center" colspan="1"><math>~0.999208</math></td>
<td align="center" colspan="1"><math>~0.019887</math></td>
<td align="center" colspan="1"><math>~0.803522</math></td>
<td align="center" colspan="1"><math>~0.509118</math></td>
<td align="center" colspan="1"><math>~0.066901</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.078</math></td>
<td align="center" colspan="1"><math>~-0.142539</math></td>
<td align="center" colspan="1"><math>~0.892548</math></td>
<td align="center" colspan="1"><math>~0.942353</math></td>
<td align="center" colspan="1"><math>~0.989322</math></td>
<td align="center" colspan="1"><math>~-0.072283</math></td>
<td align="center" colspan="1"><math>~0.810056</math></td>
<td align="center" colspan="1"><math>~0.500846</math></td>
<td align="center" colspan="1"><math>~0.020554</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.061</math></td>
<td align="center" colspan="1"><math>~-0.247448</math></td>
<td align="center" colspan="1"><math>~0.916366</math></td>
<td align="center" colspan="1"><math>~0.932024</math></td>
<td align="center" colspan="1"><math>~0.916375</math></td>
<td align="center" colspan="1"><math>~-0.186599</math></td>
<td align="center" colspan="1"><math>~0.827074</math></td>
<td align="center" colspan="1"><math>~0.505248</math></td>
<td align="center" colspan="1"><math>~-0.050956</math></td>
</tr>
<tr>
<td align="center" colspan="2"><math>~1.0449467</math></td>
<td align="center" colspan="1"><math>~-0.398902</math></td>
<td align="center" colspan="1"><math>~1.000000</math></td>
<td align="center" colspan="1"><math>~0.885198</math></td>
<td align="center" colspan="1"><math>~0.632605</math></td>
<td align="center" colspan="1"><math>~-0.220722</math></td>
<td align="center" colspan="3">Degenerate Coordinate Values</td>
</tr>
</table>
</div>
<!-- (END) Raw Text Providing Example of Wikitable Overflow -->
Digital Images
Example extracted from Wiki chapter titled: Dyson (1893)
| ||||||
Raw text used to generate this figure panel containing four (reprinted with permission) digital images:
<!-- (BEGIN) Raw Text Providing a Template for Posting Digital Images (Original or Reprinted) -->
<table border="0" cellpadding="8" align="center"><tr><td align="center">
<table border="1" cellpadding="5" align="center">
<tr><td align="center" colspan="2" bgcolor="lightgreen">
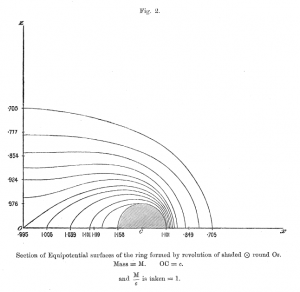
'''Figures 1, 2, 3, & 6 extracted without modification from pp. 63-66 of <br />
{{ Dyson1893figure }}
<!--
[http://adsabs.harvard.edu/abs/1893RSPTA.184...43D F. W. Dyson (1893)]'''<br />
''The Potential of an Anchor Ring''<br /> Phil. Trans. Royal Soc. London. A., Vol. 184
-->
<br />[https://doi.org/10.1098/rsta.1893.0002 https://doi.org/10.1098/rsta.1893.0002]<br />
[[File:PermissionsRectYellow.png|75px|link=Appendix/Permissions#Dyson1893]]
</td></tr>
<tr>
<td>
[[File:RoverDinfty.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = infinity]]
</td>
<td>
[[File:RoverD5over1.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 5]]
</td>
</tr>
<tr>
<td>
[[File:RoverD5over2.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 1.667]]
</td>
<td>
[[File:RoverDunity.png|300px|center|The Potential Exterior to an Anchor Ring; R/d = 1]]
</td>
</tr>
</table>
</td></tr></table>
<!-- (END) Raw Text Providing a Template for Posting Digital Images (Original or Reprinted) -->
Permissions
Here is an example layout that we have adopted to provide a record of Permissions that have been granted to us by other authors and/or publishers to reproduce figures (and/or digitally clipped images of other material) from previously published (usually journal) articles.
| 🔵 |
Wiki chapter titled: Dyson (1893) |
|||||||||||||||||
|
Here is the raw text that has been typed into our MediaWiki editor in order to generate this example Permissions layout. Generally speaking the statements of permission that we have received from various authors/publishers have been grouped in our Permissions Appendix, but this raw text can be cut (from here) and pasted into any other MediaWiki-formatted chapter to serve as a template of this adopted Permissions format.
<!-- (BEGIN) Raw Text Providing a Template for Recorded Permissions --> <table border="0" cellpadding="2" align="center" width="100%"> <tr> <td align="right" width="10%"><font size="-1">🔵</font></td> <td align="left"> Wiki chapter titled: [[Apps/DysonPotential#Evaluation|Dyson (1893)]] </td> </tr> <tr> <td align="right"> </td> <td align="left"> <table border="1" align="left" width="90%" cellpadding="5"> <tr> <td align="right" width="15%">Author(s):</td> <td align="left">F. W. (Frank Watson) Dyson</td> </tr> <tr> <td align="right">Title:</td> <td align="left">''II. The Potential of an Anchor Ring''</td> </tr> <tr> <td align="right">Reference:</td> <td align="left">[http://adsabs.harvard.edu/abs/1893RSPTA.184...43D F. W. Dyson (1893, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95)]</td> </tr> <tr> <td align="right">DOI:</td> <td align="left">[https://doi.org/10.1098/rsta.1893.0002 https://doi.org/10.1098/rsta.1893.0002]</td> </tr> <tr> <td align="right">(Scanned Images) Copyright:</td> <td align="left">© 2017, Royal Society</td> </tr> <tr> <td align="right">Publisher:</td> <td align="left">Royal Society Publishing</td> </tr> <tr> <td align="right" bgcolor="yellow">Author Permission</td> <td align="left" rowspan="2">"[https://royalsociety.org/journals/permissions/ You do not need to seek permissions for re-use of material over 70 years old for up to 5 articles or figures — re-use is only subject to acknowledgement.]"</td> </tr> <tr> <td align="right" bgcolor="yellow">Copyright Permission</td> </tr> </table> </td> </tr> </table> <!-- (END) Raw Text Providing a Template for Recorded Permissions -->
Data File Locations (Yellow)
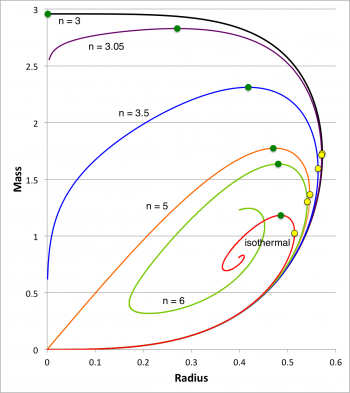
I use Microsoft Excel to generate plots that can then be (a) turned into a "png" image that is (b) uploaded for display within a MediaWiki chapter. I have found that, months (or, especially, years) after I originally created the image, I will return to the chapter and discover that I would like to modify the original plot. Often I cannot remember where I have stored the relevant Excel spreadsheet on my home-based computer's disk, or in the cloud. In an effort to solve this problem, I have created a simple, yellow "Data File" icon that can be attached to the MediaWiki figure such that, when you scroll the mouse cursor over the icon, a text box appears that explains where the file has been stored. Immediately below, I present an example: Figure 3, copied from our chapter that discusses "Turning Points along Sequences of Pressure-Truncated Polytropes."
of Pressure-Truncated Polytropes |
|---|
<table border="0" cellpadding="8" align="center"> <tr> <th align="center">[[File:DataFileButton02.png|right|60px|file = Dropbox/WorkFolder/Wiki edits/EmbeddedPolytropes/CombinedSequences.xlsx --- worksheet = EqSeqCombined]]Figure 3: Equilibrium Sequences<br />of Pressure-Truncated Polytropes </th> </tr> <tr> <td align="center" colspan="1"> [[File:MassVsRadiusCombined02.png|350px|Equilibrium sequences of Pressure-Truncated Polytropes]] </td> </tr> </table>
See Also

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |