Appendix/SpecialFunctions
 Special Functions
Special Functions
Gamma Function
|
Gamma Function |
|||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
To insert a given equation into any Wiki document, type ... |
|
||||||||||||||||||||||||||
|
Template_Name |
Resulting Equation |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
Complete Elliptic Integrals
|
Complete Elliptic Integral … |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
To insert a given equation into any Wiki document, type ... |
|
|||||||||||||
|
Template_Name |
Resulting Equation |
|||||||||||||
|
… of the First Kind
|
||||||||||||||
|
… of the First Kind (alternate expression)
|
|
|||||||||||||
|
… of the Second Kind
|
||||||||||||||
|
… of the Second Kind (alternate expression)
|
|
|||||||||||||
See also:
- W. J. Cody (1965, Mathematics of Computation, Vol. 19, No. 89, pp. 105 - 112), "Chebyshev Approximations for the Complete Elliptic Integrals K and E".
- "Chebyshev Polynomial Expansions of Complete Elliptic Integrals," by W. J. Cody (Argonne National Laboratory)
Toroidal Function Evaluations
Analytic Expressions & Plots
|
Toroidal Function Evaluations |
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
To insert a given equation into any Wiki document, type ... |
|
|||||||||||||||||||||||
|
Template_Name |
Resulting Equation |
|||||||||||||||||||||||
NOTE: We have explicitly demonstrated that an alternate, equivalent expression is:
|
 |
|||||||||||||||||||||||
|
 |
|||||||||||||||||||||||
NOTE: It appears as though an alternate, equivalent expression is:
|
 |
|||||||||||||||||||||||
|
 |
|||||||||||||||||||||||
|
 |
|||||||||||||||||||||||
|
 |
|||||||||||||||||||||||
Caption for Plots
|
Caption for Plots: Here we explain how we assembled the various plots — shown immediately above in the right-hand column of the "Toroidal Function Evaluations" table — that depict the behavior of various associated Legendre (toroidal) functions (see the related discussion) having varying half-integer degrees , , , , and (in association with a separate related discussion) having varying order , .
|
Example Recurrence Relations
The above Toroidal Function Evaluations table provides analytic expressions for the pair of foundation functions, and , and the associated pair of foundation functions, and . From either pair of foundation functions, expressions for all other zero-order, half-integer degree toroidal functions can be obtained using a relatively simple recurrence relation drawn from the "Key Equation,"
|
|
|
|
|
|
Abramowitz & Stegun (1995), p. 334, eq. (8.5.3) |
|||
|
NOTE: , as well as , satisfies this same recurrence relation. |
Specifically, letting and , for all , we have,
|
|
|
and, |
|
|
|
|
As examples, these two relations have been used to generate columns of numbers in the comparison table shown below for, respectively, the toroidal functions, and . For order-1 and order-2 toroidal functions, the above table provides analytic expressions only for (the functions of the lowest half-integer degree) and . But, as we have detailed in an accompanying discussion, additional order-1 and order-2 expressions can be straightforwardly derived by drawing upon another key recurrence relation, namely,
|
|
|
|
|
|
Abramowitz & Stegun (1995), p. 333, eq. (8.5.1) |
|||
|
NOTE: , as well as , satisfies this same recurrence relation. |
Specifically, after adopting the association, , we have, when ,
|
|
|
|
… |
for |
and, when ,
|
|
|
|
… |
for |
As an example, the first of these two relations has been used to generate a column of numbers in the comparison table shown below for the toroidal function, .
Comparison with Table IX from MF53
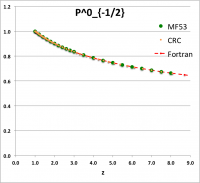
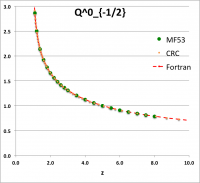
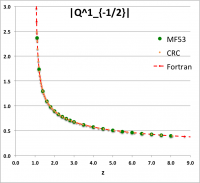
To facilitate copying & pasting for immediate use by other researchers, here we present in a tab-delimited, plain-text format the evaluation of nine separate toroidal functions: (Top half of table) , and ; (Bottom half of table) , , , , and . Each function has been evaluated for approximately 23 different argument values in the range, , and, for each function, two columns of function values have been presented: (Left column) Low-precision evaluation extracted directly from Table IX (p. 1923) of [MF53]; (Right column) Our double-precision evaluation based on a set of Numerical Recipes algorithms. One exception: The value listed under the "MF53" column for the evaluation of is the high-precision value published on p. 340 of Abramowitz & Stegun (1995); notice that our high-precision evaluation matches all ten digits of their published value.
|
Top half of Table IX (p. 1923) of [MF53] |
z P0m1Half(z) P0p1Half(z) P0p3Half(z) MF53 Our Calc. MF53 Our Calc. MF53 Our Calc. 1.0 1.0000 1.0000 1.0000 1.2 0.9763 9.763155118E-01 1.0728 1.072784040E+00 1.3910 1.391015961E+00 1.4 0.9549 9.549467781E-01 1.1416 1.141585331E+00 1.8126 1.812643692E+00 1.6 0.9355 9.355074856E-01 1.2070 1.206963827E+00 2.2630 2.263020336E+00 1.8 0.9177 9.176991005E-01 1.2694 1.269362428E+00 2.7406 2.740570128E+00 2.0 0.9013 9.012862994E-01 1.3291 1.329138155E+00 3.2439 3.243939648E+00 2.2 0.8861 8.860804115E-01 1.3866 1.386583505E+00 3.7719 3.771951476E+00 2.4 0.8719 8.719279330E-01 1.4419 1.441941436E+00 4.3236 4.323569952E+00 2.6 0.8587 8.587023595E-01 1.4954 1.495416274E+00 4.8979 4.897875630E+00 2.8 0.8463 8.462982520E-01 1.5472 1.547181667E+00 5.4941 5.494045473E+00 3.0 0.8346 8.346268417E-01 1.5974 1.597386605E+00 6.1113 6.111337473E+00 3.5 0.8082 8.081851582E-01 1.7169 1.716877977E+00 7.7427 7.742702172E+00 4.0 0.7850 7.849616703E-01 1.8290 1.828992729E+00 9.4930 9.492973996E+00 4.5 0.7643 7.643076802E-01 1.9349 1.934919997E+00 11.3555 1.135475076E+01 5.0 0.7457 7.457491873E-01 2.0356 2.035563839E+00 13.3220 1.332184253E+01 5.5 0.7289 7.289297782E-01 2.1316 2.131629923E+00 15.3890 1.538897617E+01 6.0 0.7136 7.135750093E-01 2.2237 2.223681177E+00 17.5520 1.755159108E+01 6.5 0.6995 6.994692725E-01 2.3122 2.312174942E+00 19.8060 1.980569307E+01 7.0 0.6864 6.864402503E-01 2.3975 2.397488600E+00 22.1480 2.214774685E+01 7.5 0.6743 6.743481630E-01 2.4799 2.479937758E+00 24.5750 2.457459486E+01 8.0 0.6631 6.630781433E-01 2.5598 2.559789460E+00 27.0830 2.708339486E+01 8.5 6.525347093E-01 2.637271986E+00 2.967157094E+01 9.0 6.426376817E-01 2.712582261E+00 3.233677457E+01 |
|
Bottom half of Table IX (p. 1923) of [MF53]
ATTENTION: Widen your browser window, or "zoom out," in order to obtain a proper view of the space-delimited columns of numbers in this table. |
z Q0m1Half(z) Q1m1Half(z) Q2m1Half(z) Q0p1Half(z) Q1p1Half(z) Q0p3Half(z) MF53 Our Cal. MF53 Our Calc. MF53 Our Calc. M53 Our Calc. MF53 Our Calc. MF53 Our Calc. 1.1 2.8612 2.861192872E+00 2.3661 -2.366084077E+00 10.6440 1.064378304E+01 0.9788 9.787602829E-01 1.9471 -1.947110839E+00 0.4818 4.817841242E-01 1.2 2.5010 2.500956508E+00 1.7349 -1.734890983E+00 5.6518 5.651832631E+00 0.6996 6.995548314E-01 1.2524 -1.252395745E+00 0.2856 2.856355610E-01 1.4 2.1366 2.136571733E+00 1.2918 -1.291802851E+00 3.1575 3.157491205E+00 0.4598 4.597941602E-01 0.7618 -7.618218821E-01 0.14609 1.460918547E-01 1.6 1.9229 1.922920866E+00 1.0943 -1.094337965E+00 2.3230 2.323018870E+00 0.3430 3.430180260E-01 0.5501 -5.500770475E-01 0.09080 9.079816684E-02 1.8 1.7723 1.772268479E+00 0.9748 -9.748497733E-01 1.9018 1.901788930E+00 0.2720 2.720401772E-01 0.4285 -4.284853031E-01 0.06214 6.214026586E-02 2.0 1.6566 1.656638170E+00 0.8918 -8.917931374E-01 1.6454 1.645348489E+00 0.2240 2.240142929E-01 0.3489 -3.488955345E-01 0.04516 4.515872426E-02 2.2 1.5634 1.563378886E+00 0.8293 -8.292825549E-01 1.4712 1.471197798E+00 0.18932 1.893229696E-01 0.29263 -2.926294028E-01 0.03422 3.422108228E-02 2.4 1.4856 1.485653983E+00 0.7798 -7.797558474E-01 1.3441 1.344108936E+00 0.16312 1.631167365E-01 0.25076 -2.507568731E-01 0.02676 2.675556229E-02 2.6 1.419337751 1.419337751E+00 0.7391 -7.390875295E-01 1.2465 1.246521876E+00 0.14266 1.426580119E-01 0.21842 -2.184222751E-01 0.02143 2.143519083E-02 2.8 1.3617 1.361744950E+00 0.7048 -7.048053314E-01 1.1687 1.168702464E+00 0.12628 1.262756033E-01 0.19274 -1.927423405E-01 0.01751 1.751393553E-02 3.0 1.3110 1.311028777E+00 0.6753 -6.753219405E-01 1.1048 1.104816977E+00 0.11289 1.128885424E-01 0.17189 -1.718911443E-01 0.01454 1.454457729E-02 3.5 1.2064 1.206444997E+00 0.6163 -6.163068170E-01 0.9846 9.846190928E-01 0.08824 8.824567577E-02 0.13380 -1.338040913E-01 0.00966 9.664821286E-03 4.0 1.1242 1.124201960E+00 0.5713 -5.712994484E-01 0.8990 8.990205764E-01 0.07154 7.154134054E-02 0.10819 -1.081900595E-01 0.00682 6.819829619E-03 4.5 1.0572 1.057164923E+00 0.5353 -5.353494651E-01 0.8339 8.338659751E-01 0.05957 5.956966068E-02 0.08993 -8.992645608E-02 0.00503 5.029656514E-03 5.0 1.0011 1.001077380E+00 0.5057 -5.056928088E-01 0.7820 7.819717783E-01 0.05063 5.062950976E-02 0.07634 -7.633526879E-02 0.00384 3.837604899E-03 5.5 0.9532 9.532056775E-01 0.4806 -4.806378723E-01 0.7393 7.392682950E-01 0.04374 4.373774515E-02 0.06588 -6.588433822E-02 0.00301 3.008238619E-03 6.0 0.9117 9.116962715E-01 0.4591 -4.590784065E-01 0.7033 7.032568965E-01 0.03829 3.828867029E-02 0.05764 -5.763649873E-02 0.00241 2.410605139E-03 6.5 0.87524 8.752387206E-01 0.44025 -4.402537373E-01 0.67231 6.723067009E-01 0.03389 3.389003482E-02 0.05099 -5.098806037E-02 0.00197 1.967394932E-03 7.0 0.84288 8.428751774E-01 0.42362 -4.236198508E-01 0.64530 6.453008278E-01 0.03028 3.027740449E-02 0.04553 -4.553369214E-02 0.00163 1.630716095E-03 7.5 0.81389 8.138862008E-01 0.40877 -4.087751846E-01 0.62144 6.214442864E-01 0.02727 2.726650960E-02 0.04099 -4.099183107E-02 0.00137 1.369695722E-03 8.0 0.78772 7.877190099E-01 0.39542 -3.954155185E-01 0.60015 6.001530105E-01 0.02473 2.472532098E-02 0.03716 -3.716124286E-02 0.00116 1.163753807E-03 8.5 7.639406230E-01 -3.833053056E-01 5.809864341E-01 2.255696890E-02 -3.389458114E-02 9.987731857E-04 9.0 7.422062367E-01 -3.722587645E-01 5.636047532E-01 2.068890884E-02 -3.108168349E-02 8.648271474E-04 |
Relationships Between Various Associated Legendre Functions
|
Relationships Between Various Associated Legendre Functions |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
To insert a given equation into any Wiki document, type ... |
|
|||||||||||||||||
|
Template_Name |
Resulting Equation |
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |