H BookTiledMenu
Tiled Menu

|
|---|
ATTENTION: You may need to alter your browser's magnification (zoom out and/or widen its window, for example) in order to view the most orderly layout of the "menu tiles" on this page.
Context
| Global Energy Considerations |
|---|
| Principal Governing Equations (PGEs) |
Continuity | Euler | 1st Law of Thermodynamics |
Poisson |
|---|
| Equation of State (EOS) |
Ideal Gas | Total Pressure Bond, Arnett, & Carr (1984) |
|---|
Spherically Symmetric Configurations
| (Initially) Spherically Symmetric Configurations |
|---|
| Free-Energy Index |

|
Structural Form Factors |
Free-Energy of Spherical Systems |
|---|
| One-Dimensional PGEs |
SSC Index |
|---|
Equilibrium Structures
| 1D STRUCTURE |
|---|

|
Scalar Virial Theorem |
|---|
| Hydrostatic Balance Equation |
Solution Strategies |
|---|
| Uniform-Density Sphere |
|---|
| Isothermal Sphere |
via Direct Numerical Integration |
|---|
| Isolated Polytropes |
Lane (1870) |
Known Analytic Solutions |
via Direct Numerical Integration |
via Self-Consistent Field (SCF) Technique |
|---|
| Zero-Temperature White Dwarf |
Chandrasekhar Limiting Mass (1935) |
|---|
| Virial Equilibrium of Pressure-Truncated Polytropes |
|---|
| Pressure-Truncated Configurations |
Bonnor-Ebert (Isothermal) Spheres (1955 - 56) |
Embedded Polytropes |
Equilibrium Sequence Turning-Points ♥ |

|
Turning-Points (Broader Context) |
|---|
| Free Energy of Bipolytropes (nc, ne) = (5, 1) |
|---|
| Composite Polytropes (Bipolytropes) |
Milne (1930) |
Schönberg- Chandrasekhar Mass (1942) |
Murphy (1983) Analytic (nc, ne) = (1, 5) |
Eggleton, Faulkner & Cannon (1998) Analytic (nc, ne) = (5, 1) |

|
|---|
Stability Analysis
| 1D STABILITY |
|---|
Three different approaches are used in the study of hydrodynamical stability of stars and other gravitating objects …
- The first approach is based on the use of the equations of small oscillations. In that case the problem is reduced to a search for the solution of the boundary-value problem of the Stourme-Liuville type for the linearised system of equations of small oscillations. The solutions consist of a set of eigenfrequencies and eigenfunctions. The following set of menu tiles include links to chapters where this approach has been applied to: (a) uniform-density configurations, (b) pressure-truncated isothermal spheres, (c) an isolated n = 3 polytrope, (d) pressure-truncated n = 5 configurations, and (e) bipolytropes having .
- Second, one can derive a variational principle from the equations of small oscillations. Below, an appropriately labeled (purple) menu tile links to a chapter in which the foundation for this approach is developed. With the aid of the variational principle, the problem is reduced to the search of the best trial functions; this leads to approximate eigenvalues of oscillations. In spite of the simplifications introduced by the use of the variational principle and by not solving the equations of motion exactly, the problem still remains complicated … One menu tile, below, links to a chapter in which an analytic (exact) demonstration of the variational principle's utility is provided in the context pressure-truncated n = 5 polytropes.
- The third approach is what we have already referred to as a free-energy — and associated virial theorem — analysis. When this method is used, it is not necessary to use the equations of small oscillations but, instead, the functional expression for the total energy of the momentarily stationary (but not necessarily in equilibrium) star is sufficient. The condition that the first variation of the energy vanishes, determines the state of equilibrium of the star and the positiveness of a second variation indicates stability.
If one wants to know from a stability analysis the answer to only one question — whether the model is stable or not — then the most straightforward procedure is to use the third, static method … For the application of this method, one needs to construct only equilibrium, stationary models, with no further calculation. Generally the static analysis gives no information about the shape of the modes of oscillation, but, in the vicinity of critical points, where instability sets in, this method makes it possible to find the eigenfunction of the mode which becomes unstable at the critical point. Generally in what follows, this will be referred to as the "B-KB74 conjecture;" a menu tile carrying this label is linked to a chapter in which this approach is used to analyze the onset of a dynamical instability along the equilibrium sequence of pressure-truncated n = 5 polytropes.

|
Variational Principle |
|---|
| Radial Pulsation Equation |
Example Derivations & Statement of Eigenvalue Problem |
(poor attempt at) Reconciliation |
Relationship to Sound Waves |
|---|
 |
 |
 |
|---|
| Uniform-Density Configurations |
Sterne's Analytic Sol'n of Eigenvalue Problem (1937) |

|
|---|
| Pressure-Truncated Isothermal Spheres |
via Direct Numerical Integration |

|
|---|
| Yabushita's Analytic Sol'n for Marginally Unstable Configurations (1974) |
|
|---|
| Polytropes | Isolated n = 3 Polytrope |

|
|---|
| Exact Demonstration of B-KB74 Conjecture |
Exact Demonstration of Variational Principle |
|---|
| Pressure-Truncated n = 5 Configurations |

|
|---|
| Our (2017) Analytic Sol'n for Marginally Unstable Configurations ♥ |
|
|---|
| B-KB74 Conjecture RE: Bipolytrope (nc, ne) = (5, 1) |
|---|
| BiPolytropes | Yabushita (1975) (nc, ne) = (∞, 3/2) |
Murphy & Fiedler (1985b) (nc, ne) = (1,5) |
Stability Analysis of BiPolytropes with (nc, ne) = (5, 1) |
|---|
Nonlinear Dynamical Evolution
| 1D DYNAMICS |
|---|
| Free-Fall Collapse |
|---|
| Collapse of Isothermal Spheres |
via Direct Numerical Integration |
Similarity Solution |
|---|
| Collapse of an Isolated n = 3 Polytrope |
|---|
Two-Dimensional Configurations (Axisymmetric)
| (Initially) Axisymmetric Configurations |
|---|
| Storyline |
|---|
| PGEs for Axisymmetric Systems |
|---|
Axisymmetric Equilibrium Structures
| 2D STRUCTURE |
|---|
| Constructing Steady-State Axisymmetric Configurations |
Axisymmetric Instabilities to Avoid |
Simple Rotation Profiles |
Hachisu Self-Consistent-Field [HSCF] Technique |
Solving the Poisson Equation |
|---|
| Using Toroidal Coordinates to Determine the Gravitational Potential |

|
Attempt at Simplification ♥ |
Wong's Analytic Potential (1973) |
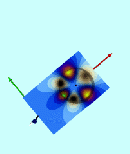
|
|---|
Spheroidal & Spheroidal-Like
| Uniform-Density (Maclaurin) Spheroids |
Maclaurin's Original Text & Analysis (1742) |
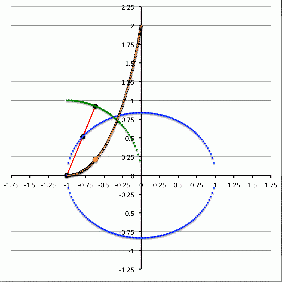
|
Maclaurin Spheroid Sequence |
Eriguchi, Hachisu & Colleagues |
|---|
| Rotationally Flattened Isothermal Configurations |
Hayashi, Narita & Miyama's Analytic Sol'n (1982) |
Review of Stahler's (1983) Sol'n Technique |
|---|
| Rotationally Flattened Polytropes |
Example Equilibria |
|---|
| Rotationally Flattened White Dwarfs |
Ostriker Bodenheimer & Lynden-Bell (1966) |
Example Equilibria |
|---|
Toroidal & Toroidal-Like
| Massless Polytropic Configurations |
Papaloizou-Pringle Tori (1984) |

|
|---|
| Self-Gravitating Incompressible Configurations |
Dyson (1893) |
Dyson-Wong Tori |
Maclaurin Toroid Sequence MPT77 |
|---|
| Self-Gravitating Compressible Configurations |
Ostriker (1964) |
|---|
Stability Analysis
| 2D STABILITY |
|---|
Sheroidal & Spheroidal-Like
| Linear Analysis of Bar-Mode Instability |
Bifurcation from Maclaurin Sequence |
Traditional Analyses |
|---|
- T. G. Cowling & R. A. Newing (1949), ApJ, 109, 149: The Oscillations of a Rotating Star
- M. J. Clement (1965), ApJ, 141, 210: The Radial and Non-Radial Oscillations of Slowly Rotating Gaseous Masses
- P. H. Roberts & K. Stewartson (1963), ApJ, 137, 777: On the Stability of a Maclaurin spheroid of small viscosity
- C. E. Rosenkilde (1967), ApJ, 148, 825: The tensor virial-theorem including viscous stress and the oscillations of a Maclaurin spheroid
- S. Chandrasekhar & N. R. Lebovitz (1968), ApJ, 152, 267: The Pulsations and the Dynamical Stability of Gaseous Masses in Uniform Rotation
- C. Hunter (1977), ApJ, 213, 497: On Secular Stability, Secular Instability, and Points of Bifurcation of Rotating Gaseous Masses
- J. N. Imamura, J. L. Friedman & R. H. Durisen (1985), ApJ, 294, 474: Secular stability limits for rotating polytropic stars
|
The equilibrium models are calculated using the polytrope version (Bodenheimer & Ostriker 1973) of the Ostriker and Mark (1968) self-consistent field (SCF) code … the equilibrium models rotate on cylinders and are completely specified by , the total angular momentum, and the specific angular momentum distribution . Here is the mass contained within a cylinder of radius centered on the rotation axis. The angular momentum distribution is prescribed in several ways: (1) imposing strict uniform rotation; (2) using the same as that of a uniformly rotating spherical polybrope of index (see Bodenheimer and Ostriker 1973); and (3) using , which we refer to as , for "linear." |
- J. R. Ipser & L. Lindblom (1990), ApJ, 355, 226: The Oscillations of Rapidly Rotating Newtonian Stellar Models
- J. R. Ipser & L. Lindblom (1991), ApJ, 373, 213: The Oscillations of Rapidly Rotating Newtonian Stellar Models. II. Dissipative Effects
- J. N. Imamura, J. L. Friedman & R. H. Durisen (2000), ApJ, 528, 946: Nonaxisymmetric Dynamic Instabilities of Rotating Polytropes. II. Torques, Bars, and Mode Saturation with Applications to Protostars and Fizzlers
- M. Shibata, S. Karino, & Y. Eriguchi (2003), MNRAS, 343, 619 - 626: Dynamical bar-mode instability of differentially rotating stars: effects of equations of state and velocity profiles
- G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche ellipsoids
Toroidal & Toroidal-Like
| Defining the Eigenvalue Problem |
|---|
| (Massless) Papaloizou-Pringle Tori |
Analytic Analysis by Blaes (1985) |
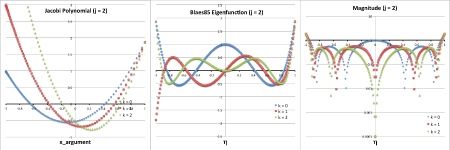 |
|---|
| Self-Gravitating Polytropic Rings |
Numerical Analysis by Tohline & Hachisu (1990) |
 |
Thick Accretion Disks (WTH94) |
Hadley & Imamura Collaboration |
|---|
Nonlinear Dynamical Evolution
Sheroidal & Spheroidal-Like
| 2D DYNAMICS |
|---|
| Free-Fall Collapse of an Homogeneous Spheroid |
|---|
| Nonlinear Development of Bar-Mode |
Initially Axisymmetric & Differentially Rotating Polytropes |
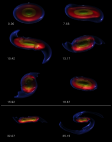
|
|---|
Two-Dimensional Configurations (Nonaxisymmetric Disks)
| Infinitesimally Thin, Nonaxisymmetric Disks |
|---|
| 2D STRUCTURE |
|---|
| Constructing Infinitesimally Thin Nonaxisymmetric Disks |
|---|
Three-Dimensional Configurations
| (Initially) Three-Dimensional Configurations |
|---|
Equilibrium Structures
| 3D STRUCTURE |
|---|
|
Special numerical techniques must be developed "to build three-dimensional compressible equilibrium models with complicated flows." To date … "techniques have only been developed to build compressible equilibrium models of nonaxisymmetric configurations for a few systems with simplified rotational profiles, e.g., rigidly rotating systems (Hachisu & Eriguchi 1984; Hachisu 1986), irrotational systems (Uryū & Eriguchi 1998), and configurations that are stationary in the inertial frame (Uryū & Eriguchi 1996)." |
|
— Drawn from §1 of 📚 S. Ou (2006, ApJ, Vol. 639, pp. 549 - 558) |
Ellipsoidal & Ellipsoidal-Like
| Steady-State 2nd-Order Tensor Virial Equations |
|---|
| Uniform-Density Incompressible Ellipsoids |
Bernhard Riemann (1861) |
|---|
| The Gravitational Potential (Ai coefficients) |
Jacobi Ellipsoids |
Riemann S-Type Ellipsoids |
Type I Riemann Ellipsoids |
Riemann meets COLLADA & Oculus Rift S |
|---|
| A Gauge Theory of Riemann Ellipsoids |
Nuclear Wobbling Motion |
|---|
| Compressible Analogs of Riemann Ellipsoids |
Ferrers Potential (1877) |
Constructing Ellipsoidal & Ellipsoidal-Like Configurations |
Thoughts & Challenges |
|---|
- B. P. Kondrat'ev (1985), Astrophysics, 23, 654: Irrotational and zero angular momentum ellipsoids in the Dirichlet problem
- 📚 D. Lai, F. A. Rasio, & S. L. Shapiro (1993b, ApJ Suppl., Vol. 88, pp. 205 - 252): Ellipsoidal Figures of Equilibrium: Compressible models
Binary Systems
- S. Chandrasekhar (1933), MNRAS, 93, 539: The equilibrium of distorted polytropes. IV. the rotational and the tidal distortions as functions of the density distribution
- 📚 S. Chandrasekhar (1963, ApJ, Vol. 138, pp. 1182 - 1213): The Equilibrium and the Stability of the Roche Ellipsoids
|
Roche's problem is concerned with the equilibrium and the stability of rotating homogeneous masses which are, further, distorted by the constant tidal action of an attendant rigid spherical mass. |
Stability Analysis
| 3D STABILITY |
|---|
Ellipsoidal & Ellipsoidal-Like
| Lebovitz & Lifschitz (1996) |
|---|
Binary Systems
- 📚 S. Chandrasekhar (1963, ApJ, Vol. 138, pp. 1182 - 1213): The Equilibrium and the Stability of the Roche Ellipsoids
- G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche Ellipsoids
Nonlinear Evolution
| 3D DYNAMICS |
|---|
|
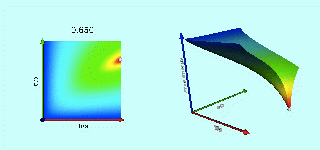
Free-Energy Evolution from the Maclaurin to the Jacobi Sequence |
|---|
| Fission Hypothesis |
"Fission" Simulations at LSU |
|---|
Secular
- M. Fujimoto (1971), ApJ, 170, 143: Nonlinear Motions of Rotating Gaseous Ellipsoids
- W. H. Press & S. A. Teukolsky (1973), ApJ, 181, 513: On the Evolution of the Secularly Unstable, Viscous Maclaurin Spheroids
- S. L. Detweiler & L. Lindblom (1977), ApJ, 213, 193: On the evolution of the homogeneous ellipsoidal figures.
Dynamical
See Also

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |