SSC/Stability/InstabilityOnsetOverview
Marginally Unstable Pressure-Truncated Gas Clouds
|
Additional details may be found here.
Isothermal
Structure
Once a central density, , and constituent fluid sound speed, , have been specified, the internal structure of an equilibrium, isothermal sphere can be completely described in terms of the function, , which is a solution of the,
subject to the boundary conditions, and at . Using numerical integration techniques, the function, , and its first derivative have been evaluated at discrete locations throughout the isothermal sphere and published by Emden (1907) and by Chandrasekhar & Wares (1949). In an accompanying discussion, we describe the steps that we have used to independently integrate this 2nd-order ODE in order to construct numerical models of equilibrium configurations for the stability analyses described herein.
In isolation, the isothermal sphere extends to infinity. But configurations of finite extent can be constructed by truncating the function, , at some radius, — such that the surface density is finite and set by the value of — and embedding the configuration in a hot, tenuous medium that exerts an "external" pressure, , uniformly across the surface of the — now, truncated — sphere. The internal structure of such a "pressure-truncated" isothermal sphere is completely describable in terms of the same function, , that describes the structure of the isolated isothermal sphere, except that beyond the function becomes physically irrelevant.
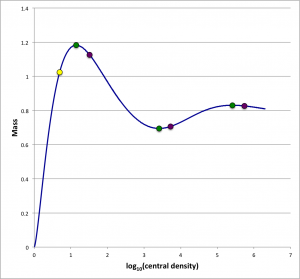
A sequence of equilibrium, pressure-truncated isothermal spheres is readily defined by varying the value of . Figure 1 displays the behavior of such an equilibrium sequence, as viewed from three different astrophysical perspectives (in all cases, is held fixed while is varied monotonically along the sequence): Left panel — A diagram showing how the truncated configuration's equilibrium volume varies with the externally applied pressure, if the configuration's mass is held fixed. Center panel — A diagram showing how the truncated configuration's mass varies with the equilibrium radius, if the external pressure is held fixed. Right panel — A diagram that shows how the configuration's mass varies with central density, if the external pressure is held fixed.
|
Figure 1: Equilibrium Sequences of Pressure-Truncated Isothermal Spheres |
||||
| ● | †External Pressure vs. Volume (Fixed Mass) |
Mass vs. Radius (Fixed External Pressure) |
‡Mass vs. Central Density (Fixed External Pressure) |
|
| ● | 4.05 |
 |
 |
 |
| ● | 6.45 | |||
| ● | 9.00 | |||
| ● | 67.00 | |||
| ● | 98.50 | |||
| ● | 735.00 | |||
| ● | 1060.00 | |||
vs.
|
vs. See also Fig. 12b of Stahler (1983) |
vs. See also Fig. 12a of Stahler (1983) |
||
|
†This is the classic P-V diagram that shows up in most discussions of Bonnor-Ebert spheres. |
||||
In Figure 1, the small, yellow circular marker identifies the configuration along each equilibrium sequence for which . In the center panel it marks the approximate location of a "turning point" along the mass-radius equilibrium sequence; specifically, it identifies the configuration along the sequence that exhibits the maximum equilibrium radius. This yellow marker does not appear to be associated with any particularly special feature of the equilibrium sequence displayed in the left figure panel or the one displayed in the panel on the right. Moving along each of the displayed sequences, past the yellow marker, one encounters a small, green circular marker that identifies the configuration for which . In the left panel, it marks the approximate location of another "turning point"; specifically, the turning point that identifies the external pressure above which no equilibrium configurations exist. This will henceforth be referred to as the -max turning point. It is clear that, in both the center panel and the right panel, this green marker is also associated with a turning point — the so-called Bonnor-Ebert limiting mass.
As we have reviewed in a separate chapter, Bonnor was the first to point out, in the context of the diagram (left panel of Figure 1), that the precise location of the -max turning point is given by the configuration for which,
We (and others before us) have determined numerically that this condition is satisfied for .
Moving still further along each Figure 1 equilibrium sequence, one encounters in succession: a purple marker ; a green marker ; a purple marker ; a green marker ; and, finally, a purple marker . The two additional green markers were specifically put in place in the left panel of Figure 1 to identify the approximate locations of additional local extrema in the external pressure; and the three purple markers were put in place to identify the approximate locations of local extrema in the configuration volume. We see from the center and right panels that the configurations identified by the green markers are also associated with additional local extrema in the mass, but the purple markers do not appear to be associated with any particularly special feature of these two equilibrium sequences.
Yabushita's Insight Regarding Stability
|
Yabushita's |
|---|
For any individual model along the equilibrium sequences depicted in Figure 1 — more specifically, for any choice of the truncation radius, — we can call upon traditional radial pulsation theory to determine the eigenvectors associated with that configuration's natural modes of radial oscillation. The determination of an eigenvector for a particular mode in a particular equilibrium model requires the simultaneous determination of how the fractional displacement, , varies with radial location throughout the configuration , and the associated (square of the) frequency of oscillation, , of that mode. Formally, in the context of pressure-truncated isothermal spheres, this is accomplished by solving the eigenvalue problem that is defined mathematically by the,
subject to the boundary conditions identified by Taff & Van Horn (1974), namely,
|
at |
and |
at . |
When pursuing this type of analysis, it is broadly appreciated that a stable mode of radial oscillation will exhibit an eigenvector with a positive value of , while an eigenvector for which is negative identifies a dynamically unstable mode of oscillation.
In an accompanying discussion, we have reviewed and replicated many aspects of the computational analysis presented by Taff & Van Horn (1974) of radial modes of oscillation in pressure-truncated isothermal spheres. They restricted their analysis to models having , that is, to models in the vicinity of the -max turning point; see the left panel of our Figure 1, above. While focusing specifically on the fundamental mode of oscillation, Taff and Van Horn showed — as had Yabushita (1968) before them — that is positive for configurations that lie to the right of the -max turning point, while it is negative for configurations that lie to the left of this turning point. This result supported the astrophysics community's widely held expectation that the -max turning point is associated with the onset of a dynamical instability in pressure-truncated isothermal spheres.
In a pair of papers that, to date, have not been widely cited, Yabushita (1974, 1975) provided solid proof that the -max turning point precisely marks the onset of dynamical instability in pressure-truncated isothermal spheres. Specifically, he showed that, if the adiabatic exponent is assigned the value, , in which case the parameter, , the following analytically defined eigenvector provides an
| Exact Solution to the Isothermal LAWE | ||
|
|
and |
|
(Note that, because , this eigenvector must be associated with a configuration that is marginally [dynamically] unstable.) In an accompanying discussion, we have demonstrated explicitly that this eigenvector is a solution to the isothermal LAWE. Along the way, we have also shown that the first logarithmic derivative of Yabushita's eigenfunction is given by the expression,
|
|
|
|
Hence, if at the surface we impose the above-specified boundary condition, namely, , then this also means that, at the surface,
|
|
|
|
And this is precisely the condition, highlighted above, that Bonnor showed was associated with the critical -max turning point along the equilibrium sequence. Hence, as Yabushita (1975) recognized, we can precisely associate the configuration at the turning point with the marginally [dynamically] unstable configuration.
Elaboration
| Figure 2: Yabushita Displacement Function |
|---|
The curves drawn in all three panels of Figure 2, shown here on the right, are identical to one another. They each trace on a semi-log plot the behavior of, what we will henceforth refer to as, the Yabushita displacement function,
|
|
|
|
While this function is formally valid over the entire coordinate range, , for practical purposes, Figure 1 only displays the function segment that extends over the radial coordinate range, to . It is worth noting, as has been demonstrated separately, that, in the limit of .
The solid, blue portion of the curve that appears in the top panel of Figure 2 extends from (near) the center of the isothermal sphere, out to the radial-coordinate location where the logarithmic derivative of the Yabushita displacement function first presents the value,
If we truncate the isothermal sphere at this radius and, accordingly, truncate at this radius as well (a short, blue vertical line segment has been drawn at this radial location to emphasize the truncation), then the (truncated) Yabushita displacement function not only satisfies the isothermal LAWE, but it also satisfies the desired surface boundary condition. We can conclude, therefore, that in tandem with the value of the eigenfrequency that accompanies Yabushita's solution — namely, — the blue curve segment in the top panel of Figure 2 represents a true eigenfunction. Because it exhibits no radial nodes, we conclude that it is the eigenfunction associated with a fundamental mode oscillation.
A small, green circular marker also appears in the top panel of Figure 2. It has been placed on the Yabushita displacement function curve at the radial-coordinate location, , corresponding to the truncation radius of the equilibrium configuration that sits at the first pressure-extremum in the left panel of Figure 1. The fact that the location of this green marker coincides with the truncation radius that naturally attends the Yabushita analysis provides a graphical illustration of the key point made above: a precise association can be made between the configuration at the -max turning point and the configuration along the equilibrium sequence whose fundamental, radial mode of oscillation has an oscillation frequency of zero and, therefore, is marginally [dynamically] unstable.
Because the Yabushita displacement function undulates back and forth between positive and negative values, we were not surprised to find that there are additional radial-coordinate locations (besides the first one, ) at which the function's logarithmic derivative equals negative three. In the middle panel of Figure 2, the blue curve segment has been extended to, and truncated at, the point along the Yabushita displacement function where the function presents, for the second time, the value,
If we truncate the isothermal sphere at this radius then, as before, the (truncated) Yabushita displacement function not only satisfies the isothermal LAWE, but it also satisfies the desired "surface" boundary condition. We can conclude, therefore, that the blue curve segment in the middle panel of Figure 2 represents another true eigenfunction. Because this eigenfunction exhibits one radial node, we conclude that it is the eigenfunction associated with a first harmonic mode of oscillation; and because the (square of the) eigenfrequency that accompanies the Yabushita displacement function is, , we conclude that the blue curve segment in the middle panel of Figure 2 is an eigenfunction of the configuration in which the first harmonic, rather than the fundamental, mode is marginally [dynamically] unstable.
But where, along the equilibrium sequence, does this configuration lie? The small, green circular marker that appears in the middle panel of Figure 2 has been placed on the Yabashita displacement function curve at the radial-coordinate location, , that corresponds to the truncation radius of the equilibrium configuration that sits at the second pressure-extremum in the left panel of Figure 1. This graphically illustrates that a direct association can be made between the configuration that sits at the second pressure extremum along the equilibrium curve and the configuration along the sequence that is marginally [dynamically] unstable to the first harmonic mode of oscillation. This is not simply a graphically approximate association but, rather, a precise one because the parameters that define both the configuration at the relevant turning point in Figure 1 and the configuration whose first harmonic mode of oscillation is displayed in the middle panel of Figure 2, satisfy the condition,
In the bottom panel of Figure 2, the blue curve segment has been extended to, and truncated at, the point along the Yabushita displacement function where the function presents, for the third time, the value,
Following a line of reasoning that is analogous to the others, just presented, we conclude that this blue curve segment represents a third true eigenfunction. This time, because the eigenfunction exhibits two radial nodes, we conclude that it is the eigenfunction associated with a second harmonic mode of oscillation; and because the (square of the) eigenfrequency that accompanies the Yabushita displacement function is, , we conclude that the blue curve segment in the bottom panel of Figure 2 is an eigenfunction of the configuration in which the second harmonic mode is marginally [dynamically] unstable. Finally, as the placement of the small, green circular dot in the bottom panel of Figure 2 illustrates, we find that there is a precise association between the configuration that sits at the third pressure extremum along the equilibrium curve and the configuration along the sequence that is marginally [dynamically] unstable to the second harmonic mode of oscillation.
Presumably many more associations of this type can be made, with the configuration located at successive pressure extrema being identified as a configuration that is marginally unstable to the next higher harmonic, radial mode of oscillation. We note, also, that although we have focused on drawing an association between configurations that are marginally unstable and configurations that sit at turning points along the curve (left panel of Figure 1), the same association can be made with configurations that sit at turning points (mass extrema) along the equilibrium curves displayed in the center panel and the right panel of Figure 1.
It is important to recognize that the physical significance of these turning points, along with the qualitative nature of the eigenfunction associated with each, has been previously deduced and described by Stahler (1983) in the context of a free-energy analysis of pressure-truncated, isothermal configurations. Specifically referring to the behavior of the equilibrium sequence in an diagram — see, for example, the right panel of our Figure 1 — Stahler concludes that (see his §IIIb), … it also follows that the first maximum in corresponds to the onset of instability in the lowest-frequency, fundamental mode (zero nodes), the first minimum to instability of the first harmonic (one node), etc. Referencing Bisnovatyi-Kogan & Blinnikov (1974), Stahler also points out that, in principle, the marginally unstable, radial-oscillation eigenvector that is associated with each of these turning points … can be computed as the zero-frequency displacement connecting neighboring equilibria. Such an analysis would, presumably, reveal the same eigenfunction that was derived by Yabushita (1975) — that is, the function defined above as, . But, as far as we are aware, such an analysis has never been completed.
Final Thought
In the above elaborative discussion, we have demonstrated that a direct association can be drawn between configurations that sit at specific equilibrium-sequence turning points and the onset of dynamical instabilities. It is important to emphasize that each such association is precise only because: (a) We have assumed that the fluid remains isothermal during radial oscillations — that is, we have set — and, (b) we have assumed that,
This precise association will break down if is set to a value other than unity, or if the discussion of turning points and dynamical instabilities is carried out within the context of a physical scenario that argues for the imposition of a quantitatively different surface boundary condition.
Polytropic
Isolated Polytropes
Given a value of the polytropic index, , the internal structure of an isolated polytrope is provided via the function, , which is a solution of the,
subject to the boundary conditions, and at . In an accompanying chapter, we have reviewed what the structural properties are of polytropes that have a range of polytropic indexes. Our emphasis has been on systems (n = 0, 1, and 5) for which the Lane-Emden equation can be solved analytically, but we also have discussed systems of astrophysical interest (n = 2.5, 3.0, 3.5, and 6) whose structural properties can only be described in terms of numerical solutions of this governing equation. In isolation, systems having extend to infinity — as does the isothermal sphere discussed above. But systems with have finite radii, that is, the function, , naturally drops to zero at a radial-coordinate location, .
Turning Points along Sequences of Pressure-Truncated Polytropes
Just as we have discussed above in the context of isothermal spheres, when , equilibrium configurations of finite extent can be constructed by truncating the function, , at some radius, — in which case the surface density is finite and set by the value of — and embedding them in a hot, tenuous medium that exerts an external pressure, , uniformly across the surface of the truncated sphere. Polytropes having may similarly be truncated at any radius, . For any value of the index, , the internal structure of each such "pressure-truncated" polytrope is completely describable in terms of the same function, , that describes the structure of an isolated polytrope with the same index, except that the function becomes physically irrelevant beyond .
of Pressure-Truncated Polytropes |
|---|
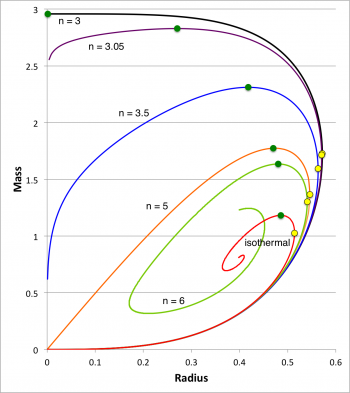
As is the case for pressure-truncated isothermal spheres, for each index, , a sequence of pressure-truncated polytropes is readily defined by varying the value of over the range, — or, as the case may be, over the range, . In an accompanying discussion of the properties of such equilibrium configurations, we have graphically displayed in a single diagram the mass-radius relation of sequences having n = 1, 2.5, 3, 3.05, 3.5, 5, and 6. In Figure 3, shown here on the right, we have redrawn these mass-radius relations for the subset of sequences that have , and have inserted as well the mass-radius relation for pressure-truncated isothermal spheres — copied from the middle panel of Figure 1, above. More specifically, adopting the mass and radius normalizations introduced by S. W. Stahler (1983), each Figure 3 polytropic sequence has been defined via the pair of parametric relations,
|
|
|
|
|
|
|
|
In Figure 3, as in Figure 1, a small, yellow circular marker has been used to identify the configuration along each sequence for which the equilibrium radius reaches its maximum value; also, a small, green circular marker identifies the configuration along each sequence that has the maximum mass. As we have reviewed in an accompanying discussion, Kimura (1981) has shown that, along each such (polytropic) mass-radius sequence, the configuration associated with the "maximum radius" turning point (yellow marker) occurs precisely where,
|
|
|
|
and the configuration associated with the "maximum mass" turning point (green marker) occurs precisely where,
|
|
|
|
As we have highlighted elsewhere, approximately a decade prior to Kimura's work, Horedt (1970) showed that this last criterion also precisely identifies the configuration that is associated with the -max turning point along polytropic pressure-volume sequences, analogous to the location of the uppermost green marker in the lefthand panel of our Figure 1. Table 3 of an accompanying discussion gives the exact, analytically determined coordinate locations of the pair of turning points that arise along the sequence, as well as approximate, numerically determined coordinate locations of the "maximum radius" (yellow markers) and "maximum mass" (green markers) turning points that have been identified along the other pressure-truncated polytropic sequences displayed in Figure 3. Because of its relevance to our discussion of stability, below, we note that, along the n = 5 sequence, the configuration that has the maximum radius (yellow marker) is truncated precisely at , while the configuration that has the maximum mass (green marker) is truncated precisely at .
Polytropic Stability
|
Our (2017) |
|---|
Setup
As we have detailed elsewhere, in order to identify individual radial oscillation modes in polytropic spheres, we seek solutions to the,
All physically reasonable solutions are subject to the inner boundary condition,
at
but the relevant outer boundary condition depends on whether the underlying equilibrium configuration is isolated (surface pressure is zero), or whether it is a "pressure-truncated" configuration. As is the case with the pressure-truncated isothermal spheres, discussed above, if the polytropic configuration is truncated by the pressure, , of a hot, tenuous external medium, then the solution to the LAWE is subject to the outer boundary condition,
at
But, for isolated polytropes — see the supporting derivation, below — the sought-after solution is subject to the more conventional boundary condition,
at
[Note added on 8/26/2021: The numerator of the first term on the RHS of this last expression used to be "n-3". This manuscript error has been fixed.]
Analyses of Radial Oscillations
In one accompanying discussion, we have reviewed and replicated many aspects of the computational analysis presented by Schwarzschild (1941) of radial modes of oscillation in isolated, n = 3 polytropic spheres. In another chapter we have presented results from our own analysis of radial oscillations in pressure-truncated, n = 5 polytropic spheres.
From Schwarzschild's work, we have come to appreciate that, if the adiabatic exponent is assigned the value, — in which case the parameter, — the following analytically defined eigenvector provides an
| Exact Solution to the (n = 3) Polytropic LAWE | ||
|
|
and |
|
that satisfies both the desired central boundary condition and the conventional surface boundary condition. This is easy to verify. Because the displacement function is unity and, therefore, independent of the radial coordinate, , its first and second derivatives — and, hence, the first two terms on the RHS of the polytropic LAWE — are zero. The third term on the RHS of the polytropic LAWE is also zero because both and are zero. Hence the sum of these three terms is zero, so the LAWE is satisfied. And, because and , we expect from the conventional surface boundary condition that at , which of course it is because the the first derivative of the displacement function is zero at all radial locations, including the surface.
In the course of our study of the properties of radial oscillations in pressure-truncated, n = 5 polytropes, we discovered that, if the adiabatic exponent is assigned the value, — in which case the parameter, — the following analytically defined eigenvector provides an
| Exact Solution to the (n = 5) Polytropic LAWE | ||
|
|
and |
|
which satisfies both of the desired boundary conditions if the configuration is truncated at the radial coordinate, . From our above reference to the n = 5 equilibrium sequence, we know that identifies the configuration that sits at the maximum-mass turning point. In this case, then, we recognize that our analytically defined eigenvector describes the properties of the (marginally unstable) fundamental mode of radial oscillation specifically for the configuration at the maximum-mass turning point — which, recall, is also the configuration at the -max turning point of the P-V sequence. Our ability to identify this analytic solution to the polytropic LAWE was significantly aided by the fact that the structural properties of the underlying equilibrium configuration are analytically specifiable.

Building on our recognition of these two analytically specifiable eigenvectors for polytropes, and Yabushita's extraordinary discovery of the set of analytically specifiable eigenvectors that are associated with pressure-truncated isothermal spheres, we have made the following additional, and more broadly applicable discovery: For any value of the polytropic index in the range,
, if the adiabatic exponent is assigned the value,
— in which case the parameter,
— the following eigenvector specification provides an,
| Exact Solution to the Polytropic LAWE | ||
|
|
and |
|
Furthermore, for all values of in this specified range, this displacement function will satisfy both of the desired boundary conditions if the associated polytropic configuration is truncated at the radial coordinate, , that satisfies the condition,
|
|
|
|
As has been pointed out, above, in the context of our discussion of equilibrium sequences, in all cases , this is a condition that also is associated with the "maximum mass" (and -max) turning point along the corresponding equilibrium sequence — see the green markers in Figure 3. We conclude, therefore, that for all polytropic indexes greater than or equal to three (including isothermal structures), the configuration that is marginally [dynamically] unstable is precisely associated with the maximum-mass and -max turning point along the relevant equilibrium sequence!
Properties of the Marginally Unstable, Fundamental-Mode Eigenfunctions
Radial Displacement Function
The right panel of Figure 4 shows how the displacement function, , varies with the radial coordinate, , for five different values of the polytropic index; specifically, as labeled, for n = 3, 3.05, 3.5, 5, and 6. These are the same index values for which mass-radius equilibrium sequences have been displayed, above, in Figure 3. The Yabushita displacement function, which is relevant to isothermal configurations, is also shown, for comparison. The same set of curves (unlabeled, but having the same colors) have been redrawn on a semi-log plot in the left panel of Figure 4; in this panel the "isothermal" curve is identical to the curve that appears in the top panel of Figure 2.
Figure 4: Fundamental-Mode Eigenfunctions |
|---|
In both panels of Figure 4, the curve associated with each polytropic index, , has been displayed in two segments: (a) A solid, colored segment that extends from the center of the configuration out to the radial location where the logarithmic derivative of the relevant displacement function first presents the value, ; and (b) a dashed, black segment that, for , continues on to the natural edge of the isolated polytrope having the same index or, for , extends to infinity. (In all cases, the outer coordinate edge of this dashed, black curve segment lies beyond the edge of the plot and is, therefore, not actually shown.) As we have just discussed, for the special case of n = 3, it is the isolated polytrope — not a pressure-truncated configuration — and the more conventional surface boundary condition that are relevant, so in Figure 4 this particular displacement function has been drawn as a solid (black) curve that extends all the way out to the natural edge of an isolated n = 3 polytrope, which — see, for example, p. 77 of Horedt (2004) — is located at .
Drawing direct parallels with our detailed discussion, above, of Yabushita's displacement function in the context of isothermal spheres, we recognize that the solid curve segments displayed in Figure 4 each:
- Represents a true eigenfunction because its associated (truncated) displacement function satisfies, both, the polytropic LAWE and the appropriate surface boundary condition;
- Identifies the radial profile of the underlying equilibrium configuration's fundamental mode of radial oscillation because it exhibits no radial nodes;
- Is associated with a configuration that is marginally [dynamically] unstable because the value of the associated (square of the) oscillation frequency is, .
On each Figure 4 curve, a small, green circular marker has been placed along the displacement function at the radial coordinate location that is associated with the maximum-mass turning point of the corresponding equilibrium sequence shown in Figure 3. In every case, this green marker sits at the same location where the transition is made from the solid segment to the dashed segment of the curve. In each case, this is a graphical illustration of the key point made earlier: A precise association can be made between the configuration at the maximum-mass (and -max) turning point and the configuration along the equilibrium sequence whose fundamental, radial mode of oscillation has an oscillation frequency of zero and, therefore, is marginally [dynamically] unstable.
Pressure and Density Displacement Functions
Referring back to the summary set of linearized governing equations, we can derive analytic expressions for the pressure, , and/or density, , displacement functions that correspond to our expression for . More specifically, from the linearized equation of continuity, we appreciate that,
Now, from our above-derived,
| Exact Solution to the Polytropic LAWE |
|
|
we see that,
|
|
||
|
|
And, from the Lane-Emden equation, we appreciate that,
|
|
||
|
|
||
|
|
||
|
|
As a result,
|
|
and,
Finally, according to the linearized (adiabatic form of the) first law of thermodynamics, . That is, when we set along with , we find that the pressure displacement function is given by the expression,
For later use (immediately below) we note as well that,
Again, from the Lane-Emden equation, we appreciate that,
|
|
Hence,
Cross-Check
Can you determine , given this expression for ?
When the square of the radial-oscillation frequency is set to zero, the linearized Euler + Poisson equations states,
|
|
||
|
|
Now, according to our accompanying discussion of the equilibrium structure of isolated polytopes,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
where,
|
|
|
|
|
|
|
Therefore,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
As a result, we find that,
and
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Q. E. D.
Displacement Functions Summary
|
Summary …
|
Related Thoughts
Déjà Vu
It should not be a surprise, but is nevertheless comforting to see, that our general expression for the polytropic displacement function,
morphs into the analytically defined, polytropic displacement functions that had previously been identified, namely, for n = 3 and n = 5 configurations. The first of these transformations is trivial to demonstrate because, when n = 3, the leading coefficient of the radially dependent portion of the expression for is zero. Hence,
In the second case, drawing on the definition of for n = 5 polytropes, as given in an accompanying chapter, we have,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Multiple Harmonics
In addition to the green circular marker, two small open circular markers have been placed along the dashed segment of the isothermal displacement function that is displayed in the left panel of Figure 4 — see also the top panel of Figure 2. As has been explained above, in connection with the center and bottom panels of Figure 2, these additional markers have been placed at the next two locations along the undulating displacement function where . They also correspond to the next two positions along the isothermal equilibrium sequence where an extremum in the mass occurs.
In the left panel of Figure 4, the undulating displacement function that provides a solution to the LAWE for pressure-truncated, n = 6 polytropic configurations has been similarly marked at the two additional locations where . It is clear that these two additional markers correspond to the next two positions along the companion n = 6 equilibrium sequence (Figure 3) where an extremum in the mass occurs. By analogy with the isothermal case, then, we can immediately identify the segments of the n = 6 displacement function that represent the eigenfunctions of the marginally unstable, first harmonic and second harmonic modes of radial oscillation. Presumably, similar undulations occur in, and precisely this same type of structural information about multiple harmonic-mode eigenfunctions can be extracted from, our analytically specified polytropic displacement function, , for configurations having any value of the polytropic index within the range, .
Configurations Having an Index Less Than Three
Up to this point, we have focused our stability analysis on pressure-truncated equilibrium sequences for which the polytropic index, , because these sequences exhibit turning points associated with physically interesting mass/pressure limits. As it turns out, if we assume that is zero, the generalized displacement function defined above also provides a solution to the polytropic LAWE when . This can be demonstrated explicitly when because the equilibrium structural function, , is expressible analytically; specifically,
Hence,
|
|
|
|
|
|
|
|
|
|
|
|
In an accompanying discussion we show that this displacement function precisely satisfies the n = 1, polytropic LAWE when .
Does this mean that at least one configuration along the equilibrium sequence of pressure-truncated, n = 1 polytropes — see the right panel of Figure 3 in an accompanying discussion — is marginally [dynamically] unstable? The answer is, "No," because, when it is evaluated at the surface of the truncated configuration, the logarithmic derivative of the displacement function ,
|
|
|
|
is positive along the entire equilibrium sequence . Hence, the desired surface boundary condition, , is not satisfied at any location along the sequence. As a consequence, this displacement function cannot serve as a physically satisfactory, radial-mode eigenfunction.
Presumably the same logic — and ultimate consequence — applies to all other equilibrium, pressure-truncated polytropic sequences that have .
Supporting Scratch Work
For isolated polytropes of finite extent, the conventionally adopted surface boundary condition is one that ensures finite-amplitude fluctuations at the surface, namely,
|
|
|
|
|
|
|
|
where, this last expression has been written in terms of the structural form factor, . Now, for polytropic configurations,
|
|
|
|
in which case this conventional surface boundary condition becomes,
|
|
|
|
If we align the adiabatic exponent with the index of the polytrope via the expression, , this becomes,
|
|
|
|
[Note added on 1/4/2019: The numerator of the first term on the RHS of this last expression used to be "n-3". This manuscript error has been fixed.]
We have already demonstrated that this is the boundary condition used by Schwarzschild (1941) in his examination of radial oscillations in n = 3 polytropes. Presumably this also matches up with the boundary condition employed by HRW66. Notice that when n = 0, this final expression reduces to , which is the surface boundary condition that we have been using to determine the eigenvectors of all pressure-truncated configurations.
References
- Mass-radius diagram constructed from a virial equilibrium analysis in which the structural form-factors are unity.

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |