ThreeDimensionalConfigurations/ChallengesPt6

Challenges Constructing Ellipsoidal-Like Configurations (Pt. 6)

This chapter has been created in February 2022, after letting this discussion lie dormant for close to one year. We begin the chapter by grabbing large segments of our earlier derivations found primarily in the "Ramblings" chapter titled, Construction Challenges (Pt. 4).

Intersection Expression

STEP #1

First, we present the mathematical expression that describes the intersection between the surface of an ellipsoid and a plane having the following properties:

• The plane cuts through the ellipsoid's z-axis at a distance, $z_0$, from the center of the ellipsoid;
• The line of intersection is parallel to the x-axis of the ellipsoid; and,
• The line that is perpendicular to the plane and passes through the z-axis at $z_0$ is tipped at an angle, $\theta$, to the z-axis.

As is illustrated in Figure 1, we will use the line referenced in this third property description to serve as the z'-axis of a Cartesian grid that is tipped at the angle, $\theta$, with respect to the body frame; and we will align the x' axis with the x-axis, so it should be clear that the z'-axis lies in the y-z plane of the ellipsoid.

Figure 1
$x$ $=$ $x^{\prime },$ $y$ $=$ $y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$ $(z-z_0)$ $=$ $z^{\prime }\cos \theta +y^{\prime }\sin \theta .$		$x^{\prime }$ $=$ $x,$ $y^{\prime }$ $=$ $y\cos \theta +(z-z_0)\sin \theta ,$ $z^{\prime }$ $=$ $(z-z_0)\cos \theta -y\sin \theta .$

As has been shown in our accompanying discussion, we obtain the following,

Intersection Expression
$1-\frac{x^2}{a^2}$	$=$	$y^2\left[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}\right]+y\left[\frac{2z_0\tan \theta }{c^2}\right]+\frac{z_0^2}{c^2},$

as long as z₀ lies within the range,

$z_0^2$

$\le$

$c^2+b^2{\tan }^2\theta .$

Rewriting this "intersection expression" in terms of the tipped (primed) coordinate frame gives us,

$1-\frac{(x^{\prime }{)}^2}{a^2}$

$=$

$(y^{\prime }\cos \theta -z^{\prime }\sin \theta {)}^2[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}]+(y^{\prime }\cos \theta -z^{\prime }\sin \theta )[\frac{2z_0\tan \theta }{c^2}]+\frac{z_0^2}{c^2}.$

STEP #2

As viewed from the tipped coordinated frame, the curve that is identified by this intersection should be an

Off-Center Ellipse
$1$	$=$	$[\frac{x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2+[\frac{y^{\prime }-y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2$
	$=$	$[\frac{x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2+[\frac{(y^{\prime }{)}^2-2y^{\prime }{y}_c+y_c^2}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}],$

that lies in the x'-y' plane — that is, $z^{\prime }=0$. Let's see if the intersection expression can be molded into this form.

$1-\frac{z_0^2}{c^2}-\frac{(x^{\prime }{)}^2}{a^2}$	$=$	$(y^{\prime }{)}^2[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}]{\cos }^2\theta +2y^{\prime }[\frac{z_0\sin \theta }{c^2}]$
	$=$	$\left[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}\right]{\cos }^2\theta \{(y^{\prime }{)}^2-2y^{\prime }\left[\frac{-z_0\sin \theta }{c^2{\cos }^2\theta }\right]\left[\frac{b^2{c}^2}{c^2+b^2{\tan }^2\theta }\right]\}$
	$=$	${\kappa }^2[(y^{\prime }{)}^2-2y^{\prime }\underset{y_c}{\underbrace{\left(\frac{-z_0\sin \theta }{c^2{\kappa }^2}\right)}}],$

RESULT 3 (same as Result 1, but different from Result 2, below)

$\frac{y_c}{z_0}$ $=$ $-\frac{\sin \theta }{c^2{\kappa }^2}$

where,

${\kappa }^2$

$\equiv$

$\frac{c^2{\cos }^2\theta +b^2{\sin }^2\theta }{b^2{c}^2}.$

Dividing through by ${\kappa }^2$, then adding $y_c^2$ to both sides gives,

$(y^{\prime }{)}^2-2y^{\prime }{y}_c+y_c^2$

$=$

$\underset{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{\underbrace{[\frac{1}{{\kappa }^2}-\frac{z_0^2}{c^2{\kappa }^2}+y_c^2]}}-\frac{(x^{\prime }{)}^2}{a^2{\kappa }^2}.$

Finally, we have,

$\frac{1}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}[(y^{\prime }{)}^2-2y^{\prime }{y}_c+y_c^2]$

$=$

$1-(x^{\prime }{)}^2\underset{1/x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{\underbrace{\left[\frac{1}{a^2{\kappa }^2{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]}}.$

So … the intersection expression can be molded into the form of an off-center ellipse if we make the following associations:

$\frac{y_c}{z_0}$ $=$ $-\frac{\sin \theta }{c^2{\kappa }^2},$ MISTAKE! (see below) …      $y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ $=$ $\frac{1}{{\kappa }^2}[1-\frac{z_0^2}{c^2}-\frac{z_0\sin \theta }{c^2}],$ MISTAKE! (see below) …      $x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ $=$ $a^2[1-\frac{z_0^2}{c^2}-\frac{z_0\sin \theta }{c^2}].$ Note as well that, $(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2$ $=$ $a^2{\kappa }^2=\frac{a^2}{b^2{c}^2}[c^2{\cos }^2\theta +b^2{\sin }^2\theta ].$

Lagrangian Trajectory and Velocities

We presume that the off-center ellipse that is defined by the intersection expression identifies the trajectory of a Lagrangian fluid element. If this is the case, there are a couple of ways that the velocity — both the amplitude and its vector orientation — can be derived.

STEP #3

If the intersection expression identifies a Lagrangian trajectory, then the velocity vector must be tangent to the off-center ellipse at every location. At each $(x^{\prime },y^{\prime })$ coordinate location, the slope of the above-defined off-center ellipse is,

$\frac{d{y}^{\prime }}{d{x}^{\prime }}$

$=$

$(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2\frac{x^{\prime }}{(y_c-y^{\prime })}.$

From this expression we deduce that the x'- and y'- components of the velocity vector are, respectively,

$\frac{{\hat{\mathit{ı}}}^{\prime }\cdot {\mathit{u}}^{\prime }}{[{\mathit{u}}^{\prime }\cdot {\mathit{u}}^{\prime }{]}^{1/2}}$

$=$

$\frac{1}{u{\text{'}}_0}\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)(y_c-y^{\prime }),$

and,

$\frac{{\hat{\mathit{ȷ}}}^{\prime }\cdot {\mathit{u}}^{\prime }}{[{\mathit{u}}^{\prime }\cdot {\mathit{u}}^{\prime }{]}^{1/2}}$

$=$

$\frac{1}{u{\text{'}}_0}\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)x^{\prime },$

where the position-dependent — and, hence also, the time-dependent — length scale,

$u{\text{'}}_0$	$\equiv$	$\left\{\right[\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)(y_c-y^{\prime }){]}^2+\left[\frac{1}{|u^{\prime }|}\right(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}})x^{\prime }{]}^2{\}}^{1/2}$
	$=$	$\frac{1}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}}[x_{\mathrm{m}\mathrm{a}\mathrm{x}}^4(y_c-y^{\prime }{)}^2+y_{\mathrm{m}\mathrm{a}\mathrm{x}}^4(x^{\prime }{)}^2{]}^{1/2}.$

STEP #4

Skipped this step on purpose.

Riemann Flow

STEP #5

Example Type I Ellipsoid (see also) $\frac{b}{a}=\frac{a_2}{a_1}$ 1.25 $\frac{c}{a}=\frac{a_3}{a_1}$ 0.4703 ${\mathrm{\Omega }}_2$ 0.3639 ${\mathrm{\Omega }}_3$ 0.6633 ${\tan }^{-1}\left[\frac{{\mathrm{\Omega }}_3}{{\mathrm{\Omega }}_2}\right]$ 61.25° ${\zeta }_2$ -2.2794 ${\zeta }_3$ -1.9637 ${\tan }^{-1}\left[\frac{{\zeta }_3}{{\zeta }_2}\right]$ 40.74° ${\beta }_{+}$ 1.13449 (1.13332) ${\gamma }_{+}$ 1.8052

As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids — see also our separate discussion — [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x₁, x₂, x₃) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating body coordinate frame, the three component expressions are,

$\dot{x}=u_1=\hat{\mathit{ı}}\cdot \mathit{u}$	$=$	$(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_{3}y-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_{2}z$	$=$	$-\left[\frac{a^2}{a^2+b^2}\right]{\zeta }_{3}y+\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_{2}z,$
$\dot{y}=u_2=\hat{\mathit{ȷ}}\cdot \mathit{u}$	$=$	$-\gamma {\mathrm{\Omega }}_{3}x$	$=$	$+\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_{3}x,$
$\dot{z}=u_3=\hat{\mathit{k}}\cdot \mathit{u}$	$=$	$+\beta {\mathrm{\Omega }}_{2}x$	$=$	$-\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_{2}x,$

where,

$\beta$

$=$

$-\left[\frac{c^2}{a^2+c^2}\right]\frac{{\zeta }_2}{{\mathrm{\Omega }}_2}$

and,

$\gamma$

$=$

$-\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{{\mathrm{\Omega }}_3}.$

In order to transform Riemann's velocity vector from the body frame (unprimed) to the "tipped orbit" frame (primed coordinates), we use the following mappings of the three unit vectors:

$\hat{\mathit{ı}}$ $\to$ ${\hat{\mathit{ı}}}^{\prime },$ $\hat{\mathit{ȷ}}$ $\to$ ${\hat{\mathit{ȷ}}}^{\prime }\cos \theta -{\hat{\mathit{k}}}^{\prime }\sin \theta ,$ $\hat{\mathit{k}}$ $\to$ ${\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathit{k}}}^{\prime }\cos \theta .$

$x$ $\to$ $x^{\prime },$ $y$ $\to$ $y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$ $z-z_0$ $\to$ $y^{\prime }\sin \theta +z^{\prime }\cos \theta .$

In the tipped frame, we find,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )]+[{\hat{\mathit{k}}}^{\prime }\sin \theta -{\hat{\mathit{ȷ}}}^{\prime }\cos \theta ]\left[\gamma {\mathrm{\Omega }}_3{x}^{\prime }\right]+[{\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathit{k}}}^{\prime }\cos \theta ]\left[\beta {\mathrm{\Omega }}_2{x}^{\prime }\right]$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )]+{\hat{\mathit{ȷ}}}^{\prime }[\beta {\mathrm{\Omega }}_2{x}^{\prime }\cdot \sin \theta -\gamma {\mathrm{\Omega }}_3{x}^{\prime }\cdot \cos \theta ]+{\hat{\mathit{k}}}^{\prime }[\beta {\mathrm{\Omega }}_2{x}^{\prime }\cdot \cos \theta +\gamma {\mathrm{\Omega }}_3{x}^{\prime }\cdot \sin \theta ].$

In order for the ${\mathit{k}}^{\prime }$ component to be zero in the tipped plane, we must choose the tipping angle such that,

$\tan \theta$

$=$

$-\frac{\beta {\mathrm{\Omega }}_2}{\gamma {\mathrm{\Omega }}_3}=-0.344793\Rightarrow \theta =-19.0238^{\circ }.$

NO!!! This is wrong! And if we examine the flow only in the tipped x'-y' plane, then we should set $z^{\prime }=-z_0/\cos \theta$. These two constraints lead to the velocity expression, ${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$ $=$ ${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta +z_0\tan \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )]+{\hat{\mathit{ȷ}}}^{\prime }[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]x^{\prime }.$

And if we examine the flow only in the tipped x'-y' plane, then we should set $z^{\prime }=0$. These two constraints lead to the velocity expression,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

$=$

${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(z_0+y^{\prime }\sin \theta )]+{\hat{\mathit{ȷ}}}^{\prime }[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]x^{\prime }.$

Graphically Compare Velocities

Using Excel, choose a particular elliptical orbit trajectory in the tipped plane, and plot the ratio of the Cartesian components of the fluid velocity as specified: (a) by EFE; and (b) by the tangent to the elliptical trajectory.

Adopting the axis-ratios, $b/a=1.25$ and $c/a=0.4703$, we can refer to the table labeled "Example Type I Ellipsoid" immediately above (under STEP #5) to obtain and/or check values of ${\mathrm{\Omega }}_2,{\mathrm{\Omega }}_3,{\zeta }_2,{\zeta }_3,{\beta }^{+},{\gamma }^{+}$. From these tabulated values, we determine that the tip angle, $\tan \theta =-0.344793\Rightarrow \theta =-0.33203$.

We then know that z₀ lies within the range,

$z_0^2$	$\le$	$c^2+b^2{\tan }^2\theta =0.40694$
$\Rightarrow -0.63792\le z_0\le +0.63792.$

As our hand-determined example, let's choose, $z_0=-0.4310$, which corresponds to the solid green ellipse that is displayed in Figure 3c of an accompanying discussion of this problem. NOTE:   Just above the referenced "Figure 3," we have stated that the limits are, z₀ = ± 0.650165; not sure why that is!

Next, we find that,

${\kappa }^2$

$\equiv$

$\frac{c^2{\cos }^2\theta +b^2{\sin }^2\theta }{b^2{c}^2}=1.05238.$

So we can evaluate a number of terms that define the relevant elliptical orbit.

CORRECTION: $y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ $=$ $\frac{1}{{\kappa }^2}-\frac{z_0^2}{c^2{\kappa }^2}+y_c^2$   $=$ $\frac{1}{{\kappa }^2}[1-\frac{z_0^2}{c^2}+\frac{z_0^2{\sin }^2\theta }{c^4{\kappa }^2}]$   $=$ $\frac{1}{c^4{\kappa }^4}[c^4{\kappa }^2-z_0^2{c}^2{\kappa }^2+z_0^2{\sin }^2\theta ]=0.51646$ $\Rightarrow y_{\mathrm{m}\mathrm{a}\mathrm{x}}$ $=$ $0.71865.$

$\frac{y_c}{z_0}$ $=$ $-\frac{\sin \theta }{c^2{\kappa }^2}=+1.40038\Rightarrow y_c=-0.60356,$ Note as well that, $(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2$ $=$ $a^2{\kappa }^2=\frac{a^2}{b^2{c}^2}[c^2{\cos }^2\theta +b^2{\sin }^2\theta ]=1.05238,$ $\Rightarrow \frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}$ $=$ $1.02585,$ $\Rightarrow x_{\mathrm{m}\mathrm{a}\mathrm{x}}$ $=$ $0.73723.$

Select points along the elliptical orbit by first specifying various values of $y^{\prime }$ over the range,

$(y_c-y_{\mathrm{m}\mathrm{a}\mathrm{x}})\le y^{\prime }\le (y_c+y_{\mathrm{m}\mathrm{a}\mathrm{x}})\Rightarrow -1.32221\le y^{\prime }\le 0.11509$

Then, for each specified value of $y^{\prime }$, calculate the corresponding value(s) of $x^{\prime }$ via the relation,

$[\frac{x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2$	$=$	$1-[\frac{y^{\prime }-y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2$
$\Rightarrow x^{\prime }$	$=$	$\pm x_{\mathrm{m}\mathrm{a}\mathrm{x}}\{1-[\frac{y^{\prime }-y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2{\}}^{1/2}.$

Orthogonality Check

Let's see if the velocity vectors associated with the Riemann steady-state flow are orthogonal to the vector that is normal to the surface of the ellipsoid, at all points.

EFE Rotating Frame

The relevant "surface" is,

$P(x,y,z)$

$=$

$(\frac{x}{a}{)}^2+(\frac{y}{b}{)}^2+(\frac{z}{c}{)}^2,$

where the constant, $0\le P(x,y,z)\le 1$. And, from above, the relevant EFE flow field is,

$\dot{x}=u_1=\hat{\mathit{ı}}\cdot \mathit{u}$	$=$	$(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_{3}y-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_{2}z$	$=$	$-\left[\frac{a^2}{a^2+b^2}\right]{\zeta }_{3}y+\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_{2}z,$
$\dot{y}=u_2=\hat{\mathit{ȷ}}\cdot \mathit{u}$	$=$	$-\gamma {\mathrm{\Omega }}_{3}x$	$=$	$+\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_{3}x,$
$\dot{z}=u_3=\hat{\mathit{k}}\cdot \mathit{u}$	$=$	$+\beta {\mathrm{\Omega }}_{2}x$	$=$	$-\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_{2}x,$

where,

$\beta$

$=$

$-\left[\frac{c^2}{a^2+c^2}\right]\frac{{\zeta }_2}{{\mathrm{\Omega }}_2}$

and,

$\gamma$

$=$

$-\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{{\mathrm{\Omega }}_3}.$

We want to determine wether the,

Orthogonality Condition
$\mathbf{𝐮}\cdot \mathrm{\nabla }P$	$=$	$0.$

is satisfied everywhere inside, and on the surface, of the ellipsoid. First, what is the expression for $\mathrm{\nabla }P$?

$\mathrm{\nabla }P$

$=$

$\hat{\mathit{ı}}\left(\frac{2x}{a^2}\right)+\hat{\mathit{ȷ}}\left(\frac{2y}{b^2}\right)+\hat{\mathbf{k}}\left(\frac{2z}{c^2}\right).$

Hence,

$\mathbf{𝐮}\cdot \mathrm{\nabla }P$	$=$	$\left(\frac{2x}{a^2}\right)\{-[\frac{a^2}{a^2+b^2}]{\zeta }_{3}y+[\frac{a^2}{a^2+c^2}\left]{\zeta }_{2}z\right\}+\left(\frac{2y}{b^2}\right)\{+[\frac{b^2}{a^2+b^2}\left]{\zeta }_{3}x\right\}+\left(\frac{2z}{c^2}\right)\{-[\frac{c^2}{a^2+c^2}\left]{\zeta }_{2}x\right\}$
	$=$	$\left(\frac{2x}{a^2}\right)\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_{2}z-\left(\frac{2x}{a^2}\right)\left[\frac{a^2}{a^2+b^2}\right]{\zeta }_{3}y+\left(\frac{2y}{b^2}\right)\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_{3}x-\left(\frac{2z}{c^2}\right)\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_{2}x$
	$=$	$\left[\frac{2{\zeta }_{2}xz}{a^2+c^2}\right]-\left[\frac{2{\zeta }_{3}xy}{a^2+b^2}\right]+\left[\frac{2{\zeta }_{3}xy}{a^2+b^2}\right]-\left[\frac{2{\zeta }_{2}xz}{a^2+c^2}\right]$
	$=$	$0.$

Tipped Frame

For Arbitrary Tip Angles

Given that,

$x$	$=$	$x^{\prime },$
$y$	$=$	$y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$
$(z-z_0)$	$=$	$z^{\prime }\cos \theta +y^{\prime }\sin \theta ,$

the constraint becomes,

$P^{\prime }(x^{\prime },y^{\prime },z^{\prime })$

$=$

$[\frac{y^{\prime }\cos \theta -z^{\prime }\sin \theta }{b}{]}^2+[\frac{z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta }{c}{]}^2+(\frac{x^{\prime }}{a}{)}^2.$

Hence,

$\mathrm{\nabla }{P}^{\prime }(x^{\prime },y^{\prime },z^{\prime })$

$=$

${\hat{\mathit{ı}}}^{\prime }\left(\frac{2x^{\prime }}{a^2}\right)+{\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\cos \theta }{b^2}]+[\frac{2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\sin \theta }{c^2}\left]\right\}+{\hat{\mathbf{k}}}^{\prime }\{-[\frac{2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\sin \theta }{b^2}]+[\frac{2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\cos \theta }{c^2}\left]\right\}.$

And, in the tipped frame we find,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{\prime }\{-[\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )\}$
		$+[{\hat{\mathit{ȷ}}}^{\prime }\cos \theta -{\hat{\mathbf{k}}}^{\prime }\sin \theta ]\left\{\right[\frac{b^2}{a^2+b^2}\left]{\zeta }_3{x}^{\prime }\right\}+[{\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathbf{k}}}^{\prime }\cos \theta ]\{-[\frac{c^2}{a^2+c^2}\left]{\zeta }_2{x}^{\prime }\right\}.$

As a result, we find,

${{\mathbf{𝐮}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}\cdot \mathrm{\nabla }{P}^{\prime }$	$=$	$\left(\frac{2x^{\prime }}{a^2}\right)\{-[\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+[\frac{a^2}{a^2+c^2}]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )\}$
		$+\left\{\right[\frac{b^2}{a^2+b^2}]{\zeta }_3\cos \theta x^{\prime }-[\frac{c^2}{a^2+c^2}]{\zeta }_2\sin \theta x^{\prime }\}\left\{\right[\frac{2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\cos \theta }{b^2}]+[\frac{2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\sin \theta }{c^2}\left]\right\}$
		$-\left\{\right[\frac{b^2}{a^2+b^2}]{\zeta }_3\sin \theta x^{\prime }+[\frac{c^2}{a^2+c^2}]{\zeta }_2\cos \theta x^{\prime }\}\{-[\frac{2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\sin \theta }{b^2}]+[\frac{2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\cos \theta }{c^2}\left]\right\}$
$\Rightarrow \left[\frac{1}{2x^{\prime }}\right]{{\mathbf{𝐮}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}\cdot \mathrm{\nabla }{P}^{\prime }$	$=$	$-\left[\frac{1}{a^2+b^2}\right]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+\left[\frac{1}{a^2+c^2}\right]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )$
		$+\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_3\left\{\right[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta ){\cos }^{}\theta }{b^2}]+[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\sin \theta \cos \theta }{c^2}\left]\right\}-\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_2\left\{\right[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\sin \theta \cos \theta }{b^2}]+[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta ){\sin }^{}\theta }{c^2}\left]\right\}$
		$+\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_3\left\{\right[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta ){\sin }^{}\theta }{b^2}]-[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\sin \theta \cos \theta }{c^2}\left]\right\}+\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_2\left\{\right[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\sin \theta \cos \theta }{b^2}]-[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta ){\cos }^{}\theta }{c^2}\left]\right\}$
	$=$	$-\left[\frac{1}{a^2+b^2}\right]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+\left[\frac{1}{a^2+c^2}\right]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )$
		$+\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_3\left[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta )}{b^2}\right]-\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_2\left[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )}{c^2}\right]$
	$=$	$\left[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta )}{a^2+b^2}\right]{\zeta }_3-\left[\frac{1}{a^2+b^2}\right]{\zeta }_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )+\left[\frac{1}{a^2+c^2}\right]{\zeta }_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )-\left[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )}{a^2+c^2}\right]{\zeta }_2$
	$=$	$0.$

Q. E. D.

For Specific Tip Angle

So … we have demonstrated that the velocity vectors are everywhere orthogonal to the normal to the ellipsoid for all values of the "tip" angle, $\theta$. So why have we been unable to demonstrate the same result in the case where,

$\tan \theta$

$=$

$-\frac{\beta {\mathrm{\Omega }}_2}{\gamma {\mathrm{\Omega }}_3}=-\left[\frac{c^2(a^2+b^2)}{b^2(a^2+c^2)}\right]\frac{{\zeta }_2}{{\zeta }_3}.$

Remember that,

$1+{\tan }^2\theta$	$=$	$\frac{{\sin }^2\theta +{\cos }^2\theta }{{\cos }^2\theta }=\frac{1}{{\cos }^2\theta }$
$\Rightarrow {\cos }^2\theta =\frac{1}{1+{\tan }^2\theta }$	and,	${\sin }^2\theta =\frac{{\tan }^2\theta }{1+{\tan }^2\theta }.$

Rearranging terms in the expression for the "tipped plane" Riemann flow velocity, we have,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{\prime }\{-\cos \theta [\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }-z^{\prime }\tan \theta )+\cos \theta [\frac{a^2}{a^2+c^2}]{\zeta }_2(y^{\prime }\tan \theta +z^{\prime })+[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}$
		$+{\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{b^2}{a^2+b^2}]{\zeta }_3-\tan \theta [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}{x}^{\prime }\cos \theta -{\hat{\mathbf{k}}}^{\prime }\{\tan \theta [\frac{b^2}{a^2+b^2}]{\zeta }_3+[\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right\}{x}^{\prime }\cos \theta$
	$=$	${\hat{\mathit{ı}}}^{\prime }\{-\cos \theta [\frac{a^2}{a^2+b^2}]{\zeta }_3(y^{\prime }-z^{\prime }\tan \theta )+\cos \theta [\frac{a^2}{a^2+c^2}]{\zeta }_2(y^{\prime }\tan \theta +z^{\prime })+[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}$
		$+{\hat{\mathit{ȷ}}}^{\prime }\{1-\tan \theta [\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right[\frac{a^2+b^2}{b^2}\left]\frac{1}{{\zeta }_3}\right\}{x}^{\prime }\cos \theta \left[\frac{b^2}{a^2+b^2}\right]{\zeta }_3-{\hat{\mathbf{k}}}^{\prime }\{\tan \theta +[\frac{c^2}{a^2+c^2}\left]{\zeta }_2\right[\frac{a^2+b^2}{b^2}\left]\frac{1}{{\zeta }_3}\right\}{x}^{\prime }\cos \theta \left[\frac{b^2}{a^2+b^2}\right]{\zeta }_3$

Then, for this specific tip angle, the Riemann flow velocity is,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{\prime }\left\{\right[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}+{\hat{\mathit{ı}}}^{\prime }\{{\zeta }_3(z^{\prime }\tan \theta -y^{\prime })\cos \theta +\cos \theta [\frac{a^2+b^2}{a^2+c^2}]{\zeta }_2(y^{\prime }\tan \theta +z^{\prime })\}\left[\frac{a^2}{a^2+b^2}\right]$
		$+{\hat{\mathit{ȷ}}}^{\prime }\{1+{\tan }^2\theta \}{x}^{\prime }\cos \theta \left[\frac{b^2}{a^2+b^2}\right]{\zeta }_3-{\hat{\mathbf{k}}}^{\prime }\left\{0\right\}$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left\{\right[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}+{\hat{\mathit{ı}}}^{\prime }\{{\zeta }_3(z^{\prime }\tan \theta -y^{\prime })\cos \theta -\cos \theta [\frac{b^2{\zeta }_3\tan \theta }{c^2{\zeta }_2}]{\zeta }_2(y^{\prime }\tan \theta +z^{\prime })\}\left[\frac{a^2}{a^2+b^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3{x}^{\prime }}{\cos \theta }$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left\{\right[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}+{\hat{\mathit{ı}}}^{\prime }\{c^2(z^{\prime }\tan \theta -y^{\prime })\cos \theta -b^2\sin \theta (y^{\prime }\tan \theta +z^{\prime })\}\frac{{\zeta }_3}{c^2}\left[\frac{a^2}{a^2+b^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3{x}^{\prime }}{\cos \theta }$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left\{\right[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}+{\hat{\mathit{ı}}}^{\prime }\{z^{\prime }(c^2-b^2)\tan \theta -y^{\prime }[c^2+b^2{\tan }^{}\theta ]\}\frac{{\zeta }_3\cos \theta }{c^2}\left[\frac{a^2}{a^2+b^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3{x}^{\prime }}{\cos \theta }$

As we have already stated,

$\mathrm{\nabla }{P}^{\prime }(x^{\prime },y^{\prime },z^{\prime })$

$=$

${\hat{\mathit{ı}}}^{\prime }\left(\frac{2x^{\prime }}{a^2}\right)+{\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\cos \theta }{b^2}]+[\frac{2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\sin \theta }{c^2}\left]\right\}+{\hat{\mathbf{k}}}^{\prime }\{-[\frac{2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\sin \theta }{b^2}]+[\frac{2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\cos \theta }{c^2}\left]\right\}.$

Hence,

$\left(\frac{1}{2x^{\prime }}\right){{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}\cdot \mathrm{\nabla }{P}^{\prime }$	$=$	$\left(\frac{1}{a^2}\right)\left\{\right[\frac{a^2}{a^2+c^2}\left]{\zeta }_2{z}_0\right\}+\left(\frac{1}{a^2}\right)\{z^{\prime }(c^2-b^2)\tan \theta -y^{\prime }[c^2+b^2{\tan }^{}\theta ]\}\frac{{\zeta }_3\cos \theta }{c^2}\left[\frac{a^2}{a^2+b^2}\right]$
		$+\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{\cos \theta }\left\{\right[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\cos \theta }{b^2}]+[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\sin \theta }{c^2}\left]\right\}$
	$=$	$-\left[\frac{{\zeta }_3}{c^2(a^2+b^2)}\right]b^2{z}_0\tan \theta +\{z^{\prime }(c^2-b^2)\tan \theta -y^{\prime }[c^2+b^2{\tan }^{}\theta ]\}\cos \theta \left[\frac{{\zeta }_3}{c^2(a^2+b^2)}\right]$
		$+\left[\frac{{\zeta }_3}{c^2(a^2+b^2)}\right]\frac{1}{\cos \theta }\left\{\right[c^2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\cos \theta ]+[b^2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\sin \theta \left]\right\}$
$\Rightarrow \left[\frac{c^2(a^2+b^2)}{{\zeta }_3}\right]\left(\frac{1}{2x^{\prime }}\right){{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}\cdot \mathrm{\nabla }{P}^{\prime }$	$=$	$-b^2{z}_0\tan \theta +\{z^{\prime }(c^2-b^2)\tan \theta -y^{\prime }[c^2+b^2{\tan }^{}\theta ]\}\cos \theta +[c^2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )]+[b^2(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\tan \theta ]$
	$=$	$\{z^{\prime }(c^2-b^2)\tan \theta -y^{\prime }[c^2+b^2{\tan }^{}\theta ]\}\cos \theta +[c^2(y^{\prime }\cos \theta -z^{\prime }\sin \theta )]+[b^2(z^{\prime }\cos \theta +y^{\prime }\sin \theta )\tan \theta ]$
	$=$	$y^{\prime }\cos \theta [-c^2-b^2{\tan }^{}\theta +c^2+b^2{\tan }^{}\theta ]+z^{\prime }[(c^2-b^2)\sin \theta -c^2\sin \theta +b^2\sin \theta ]$
	$=$	$0.$

With Help From Excel Spreadsheet

file = Dropbox/3Dviewers/RiemannModels/RiemannCalculations.xlsx --- worksheet = TypeI_1d

Here, as an example, we consider the properties of a Riemann Type I ellipsoid whose semi-axes are

$(a,b,c)=(1.0000,1.2500,0.4703)$

. Many properties of this particular model have been stored in the Dropbox location identified by scrolling your cursor over the yellow "Data Files" icon shown here, on the left.

Body Frame of Riemann Type I Ellipsoid

We recognize that, in the body frame of a Riemann ellipsoid, the surface of the configuration is defined by the following expression:

$1$

$=$

$(\frac{x}{a}{)}^2+(\frac{y}{b}{)}^2+(\frac{z}{c}{)}^2$

Blue (x = 0) Ellipse

By setting $x=z=0$, we find the point where the y-axis intersects the surface of the ellipsoid, namely,

$1$

$=$

$(\frac{y}{b}{)}^2\Rightarrow y=y_{\mathrm{m}\mathrm{a}\mathrm{x}}=b.$

Similarly, by setting $x=y=0$, we find the point where the z-axis intersects the surface of the ellipsoid, namely,

$1$

$=$

$(\frac{z}{c}{)}^2\Rightarrow z=z_{\mathrm{m}\mathrm{a}\mathrm{x}}=c.$

If we only set, $x=0$, this expression generates an ellipse in the y-z plane whose semi-axes are $(y_{\mathrm{m}\mathrm{a}\mathrm{x}},z_{\mathrm{m}\mathrm{a}\mathrm{x}})=(1.25,0.4703)$. The $(y,z)$ coordinates of individual points along the ellipse can be determined by choosing values of $y$ in the range,

$-y_{\mathrm{m}\mathrm{a}\mathrm{x}}\le y\le +y_{\mathrm{m}\mathrm{a}\mathrm{x}},$

then determining the corresponding pair of values of $z$ via the expression,

$z_{\pm }$

$=$

$\pm z_{\mathrm{m}\mathrm{a}\mathrm{x}}[1-\frac{y^2}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{]}^{1/2}.$

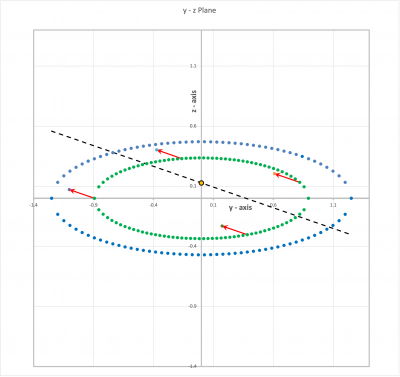
This ellipse is identified in Figure 2 by the dotted-blue curve.

Figure 2:   Y-Z plane(s) of Riemann Type I Ellipsoid file = Dropbox/3Dviewers/RiemannModels/RiemannCalculations.xlsx --- worksheet = Feb22
Blue ellipse (x/a = 0.0); Green ellipse (x/a = + 0.70)	Blue ellipse (x/a = 0.0); Green ellipse (x/a = - 0.85)

Green (x/a = 0.7) Ellipse

Next, let's examine the surface-intersection-ellipse that results from a y-z plane that slices through the ellipsoid at $x/a=0.7$. By setting $z=0$, we find the point where the y-axis intersects the surface of the ellipsoid, namely,

$1-(0.7{)}^2$

$=$

$(\frac{y}{b}{)}^2\Rightarrow y=y_{\mathrm{m}\mathrm{a}\mathrm{x}}=b[1-(0.7{)}^2{]}^{1/2}=0.89268.$

Similarly, by setting $y=0$, we find,

$1-(0.7{)}^2$

$=$

$(\frac{z}{c}{)}^2\Rightarrow z=z_{\mathrm{m}\mathrm{a}\mathrm{x}}=c[1-(0.7{)}^2{]}^{1/2}=0.33586.$

The $(y,z)$ coordinates of individual points along this ellipse can be determined, as before, by choosing values of $y$ in the range,

$-y_{\mathrm{m}\mathrm{a}\mathrm{x}}\le y\le +y_{\mathrm{m}\mathrm{a}\mathrm{x}},$

then determining the corresponding pair of values of $z$ via the expression,

$z_{\pm }$

$=$

$\pm z_{\mathrm{m}\mathrm{a}\mathrm{x}}[1-(0.7{)}^2-\frac{y^2}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{]}^{1/2}.$

This ellipse is identified in Figure 2 by the dotted-green curve. All four of the red arrows (velocity vectors, as explained below) that are displayed in Figure 2 are anchored on this dotted-green curve; the $(x,y,z{)}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$ coordinates of these anchor positions are listed in the yellow-colored elements of the following Table titled, "Red Arrows." (There is nothing special about these four chosen anchor positions other than they lie on the dotted-green ellipse.)

Red Arrows (Velocity Components in an y-z Plane)
Number	Base of each Arrow					Velocity			Arrow Tips
	$x$	$y$	$z$	$(\frac{x}{a}{)}^2+(\frac{y}{b}{)}^2+(\frac{z}{c}{)}^2$		$\dot{y}=u_2$	$\dot{z}=u_3$		$x$	$y$	$z$
1	0.7	-0.89268	0.00000	1.00000		-1.19738 x	+0.41285 x		0.7	-1.10222	+0.07225
2	0.7	-0.16396	+0.33015	1.00001					0.7	-0.37350	+0.40240
3	0.7	+0.81981	+0.13291	1.00000					0.7	+0.61027	+0.20516
4	0.7	+0.38258	-0.30345	0.99999					0.7	+0.17304	-0.23121

As a check, we have also included in the "Red Arrows" table a column that tallies,

$\left[\right(\frac{x}{a}{)}^2+(\frac{y}{b}{)}^2+(\frac{z}{c}{)}^2{]}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}},$

which in every case totals 1.000, as it should.

Velocity Components

In steady-state, the velocity that is associated with each coordinate location can be ascertained from our above STEP #5 discussion of the Riemann Flow. Here we are especially interested in the velocity components that are in an x = constant, y-z plane, that is,

$\dot{y}=u_2$	$=$	$+\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_{3}x=+\left[\frac{(1.25{)}^2}{1+(1.25{)}^2}\right](-1.9637)x=-1.19738x,$
$\dot{z}=u_3$	$=$	$-\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_{2}x=-\left[\frac{(0.4703{)}^2}{1+(0.4703{)}^2}\right](-2.2794)x=+0.41285x.$

Given that all of the points along the black-dotted ellipse in our Red Arrows figure are positioned in the $x=0$, y-z plane, we appreciate that $u_2=u_3=0$ at all points along this black ellipse. But along the green-dotted ellipse, for which $x/a=0.7$, each fluid element exhibits a nonzero component of motion in the relevant y-z plane; specifically, for all points along the green ellipse,

$u_2{|}_{x=0.7}$	$=$	$-0.83816,$
$u_3{|}_{x=0.7}$	$=$	$+0.28899.$

The pointed tip of each of the four red arrows in our figure is located at a coordinate position, $(y_{\mathrm{t}\mathrm{i}\mathrm{p}},z_{\mathrm{t}\mathrm{i}\mathrm{p}})$, determined from the following pair of expressions:

$y_{\mathrm{t}\mathrm{i}\mathrm{p}}$	$=$	$y_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}+\frac{1}{4}{u}_2{|}_{x=0.7}=y_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}-\frac{1}{4}(0.83817),$
$z_{\mathrm{t}\mathrm{i}\mathrm{p}}$	$=$	$z_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}+\frac{1}{4}{u}_2{|}_{x=0.7}=z_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}+\frac{1}{4}(0.28899).$

That is, each arrow illustrates how far a fluid element would travel away from its base location if it moved at the prescribed velocity for a time, $\mathrm{\Delta }t=\frac{1}{4}\times [\pi G\rho {]}^{-1/2}$. The four red arrows serve to illustrate that, at every point along the dotted-green ellipse, the component of the velocity that lies in the y-z plane is precisely the same, in both magnitude and direction.

Primed Coordinates

Now, if we were to examine in a similar manner the component of the fluid motion in any other x = constant, y-z plane, we would find that the red velocity vectors arising from every base point along the relevant ellipse in this new y-z plane would be the same — in both magnitude and direction — around the entire ellipse. Relative to the (dotted green) ellipse that lies in the x = 0.7, y-z plane, the magnitudes would be different — larger for larger values of

$x$

and smaller for smaller values of

$x$

— however, all of the red arrows in the new y-z plane would point in the same direction as the red arrows displayed in Figure 2.

All of the "red arrow" flow-components are tipped up, out of the x-y plane by an angle that is given by the ratio of the pair of velocity components, $(u_2,u_3)$. Specifically,

$\tan \theta$	$=$	$\frac{u_3}{u_2}=\frac{+0.41285x}{-1.19738x}=-0.34479,$
$\Rightarrow \theta$	$=$	$-0.33203$ radians $=-19.024^{\circ }.$

Borrowing from Figure 1, above, and appreciating that $\theta$ is negative in the example being used here, we would find that all of the red arrows, in all of the x = constant, y-z planes would lie parallel to the $y^{\prime }$ axis. In our Figure 2, above, the black, dashed line serves to illustrate one such $y^{\prime }$ axis; it has been drawn using the expression,

$z$

$=$

$y\tan \theta +z_0,$

where we have set $\tan \theta =-0.34479$ and $z_0=0.12758$ for $-1.25\le y\le +1.25$.

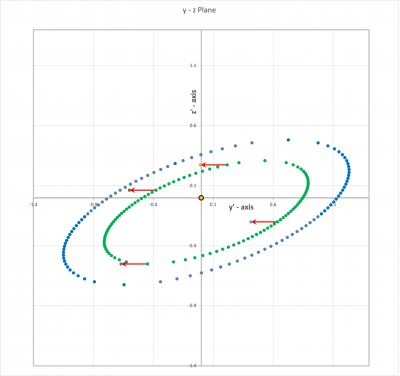
Tipped Frame

Let's continue to examine the x' = x = constant, y'-z' plane, and set $\tan \theta =-0.34479$ and $z_0=0.12758$.

Draw Tilted Ellipse

So, for a fixed value of $x^{\prime }$ and over this range in $z^{\prime }$, the value of $y^{\prime }$ is obtained from the expression,

$1$

$=$

$(\frac{x}{a}{)}^2+(\frac{y}{b}{)}^2+(\frac{z}{c}{)}^2.$

Given that,

$x$	$=$	$x^{\prime },$
$y$	$=$	$y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$
$(z-z_0)$	$=$	$z^{\prime }\cos \theta +y^{\prime }\sin \theta ,$

the constraint becomes,

$0$	$=$	$[\frac{y^{\prime }\cos \theta -z^{\prime }\sin \theta }{b}{]}^2+[\frac{z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta }{c}{]}^2+(\frac{x^{\prime }}{a}{)}^2-1$
$\Rightarrow 0$	$=$	$c^2[y^{\prime }\cos \theta -z^{\prime }\sin \theta {]}^2+b^2[z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta {]}^2+b^2{c}^2\left[\right(\frac{x^{\prime }}{a}{)}^2-1]$
	$=$	$c^2[(y^{\prime }{)}^2{\cos }^2\theta -2y^{\prime }{z}^{\prime }\sin \theta \cos \theta +(z^{\prime }{)}^2{\sin }^{}\theta ]+b^2[(z_0+z^{\prime }\cos \theta {)}^2+2y^{\prime }\sin \theta (z_0+z^{\prime }\cos \theta )+(y^{\prime }{)}^2{\sin }^{}\theta ]+b^2{c}^2\left[\right(\frac{x^{\prime }}{a}{)}^2-1]$
	$=$	$(y^{\prime }{)}^2[c^2{\cos }^2\theta +b^2{\sin }^2\theta ]+y^{\prime }[2b^2\sin \theta (z_0+z^{\prime }\cos \theta )-2c^2{z}^{\prime }\sin \theta \cos \theta ]+b^2(z_0+z^{\prime }\cos \theta {)}^2+c^2(z^{\prime }{)}^2{\sin }^{}\theta +b^2{c}^2[(\frac{x^{\prime }}{a}{)}^2-1]$
	$=$	$A(y^{\prime }{)}^2+B{y}^{\prime }+C,$

where,

$A$	$\equiv$	$c^2{\cos }^2\theta +b^2{\sin }^2\theta ,$
$B$	$\equiv$	$2b^2\sin \theta (z_0+z^{\prime }\cos \theta )-2c^2{z}^{\prime }\sin \theta \cos \theta ,$
$C$	$\equiv$	$b^2(z_0+z^{\prime }\cos \theta {)}^2+c^2(z^{\prime }{)}^2{\sin }^{}\theta +b^2{c}^2\left[\right(\frac{x^{\prime }}{a}{)}^2-1].$

In which case,

$y^{\prime }$

$=$

$\frac{B}{2A}\{-1\pm [1-\frac{4AC}{B^2}{]}^{1/2}\}.$

At what value(s) of $z^{\prime }$ do we find that, $B^2=4AC$?

$B^2$ $=$ $4AC$ $\Rightarrow 0$ $=$ $[b^2\sin \theta (z_0+z^{\prime }\cos \theta )-c^2{z}^{\prime }\sin \theta \cos \theta {]}^2-[c^2{\cos }^{}\theta +b^2{\sin }^{}\theta \left]\right[b^2(z_0+z^{\prime }\cos \theta {)}^2+c^2(z^{\prime }{)}^2{\sin }^{}\theta -b^2{c}^2{ϵ}^2]$   $=$ $[b^2\sin \theta (z_0+z^{\prime }\cos \theta ){]}^2-2[b^2\sin \theta (z_0+z^{\prime }\cos \theta )c^2{z}^{\prime }\sin \theta \cos \theta ]+[c^2{z}^{\prime }\sin \theta \cos \theta {]}^2$     $-[c^2{\cos }^2\theta +b^2{\sin }^2\theta ][b^2(z_0+z^{\prime }\cos \theta {)}^2]-[c^2{\cos }^{}\theta +b^2{\sin }^{}\theta \left]\right[c^2(z^{\prime }{)}^2{\sin }^{}\theta -b^2{c}^2{ϵ}^2]$   $=$ $b^4{\sin }^2\theta (z_0+z^{\prime }\cos \theta {)}^2-2b^2{c}^2(z^{\prime }){\sin }^{}\theta \cos \theta (z_0+z^{\prime }\cos \theta )+c^4(z^{\prime }{)}^2{\sin }^{}\theta {\cos }^{}\theta$     $-b^2{c}^2{\cos }^2\theta (z_0+z^{\prime }\cos \theta {)}^2-b^4{\sin }^{}\theta (z_0+z^{\prime }\cos \theta {)}^2-c^4(z^{\prime }{)}^2{\sin }^{}\theta {\cos }^{}\theta -b^2{c}^2(z^{\prime }{)}^2{\sin }^{}\theta +b^2{c}^2{ϵ}^2(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )$   $=$ $-2b^2{c}^2{z}_0(z^{\prime }){\sin }^2\theta \cos \theta -2b^2{c}^2(z^{\prime }{)}^2{\sin }^{}\theta {\cos }^{}\theta +c^4(z^{\prime }{)}^2{\sin }^{}\theta {\cos }^{}\theta$     $-b^2{c}^2{\cos }^2\theta [z_0^2+2z_0(z^{\prime })\cos \theta +(z^{\prime }{)}^2{\cos }^{}\theta ]-c^4(z^{\prime }{)}^2{\sin }^{}\theta {\cos }^{}\theta -b^2{c}^2(z^{\prime }{)}^2{\sin }^{}\theta +b^2{c}^2{ϵ}^2(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )$   $=$ $[c^4{\sin }^2\theta {\cos }^2\theta -2b^2{c}^2{\sin }^2\theta {\cos }^2\theta -b^2{c}^2{\cos }^4\theta -c^4{\sin }^2\theta {\cos }^2\theta -b^2{c}^2{\sin }^4\theta ](z^{\prime }{)}^2$     $-2z_0{b}^2{c}^2\cos \theta [{\cos }^{}\theta +{\sin }^{}\theta ](z^{\prime })+b^2{c}^2{ϵ}^2(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )-z_0^2{b}^2{c}^2{\cos }^{}\theta$   $=$ $-b^2{c}^2[2{\sin }^2\theta {\cos }^2\theta +{\cos }^4\theta +{\sin }^4\theta ](z^{\prime }{)}^2-2z_0{b}^2{c}^2\cos \theta (z^{\prime })+b^2{c}^2{ϵ}^2(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )-z_0^2{b}^2{c}^2{\cos }^{}\theta .$ Hence, after dividing through by $(-b^2{c}^2)$, $0$ $=$ $(z^{\prime }{)}^2+2z_0\cos \theta (z^{\prime })+z_0^2{\cos }^{}\theta -{ϵ}^2(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )$ $\Rightarrow \frac{z^{\prime }}{z_0\cos \theta }$ $=$ $\pm \{1-\frac{z_0^2{\cos }^2\theta -{ϵ}^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{z_0^2{\cos }^2\theta }{\}}^{1/2}-1$   $=$ $\pm \{\frac{{ϵ}^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{z_0^2{\cos }^2\theta }{\}}^{1/2}-1$ $\Rightarrow z^{\prime }$ $=$ $\pm ϵ(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}-z_0\cos \theta =-0.12061\pm 0.60307=(0.48246,-0.72369)$

Limits on z'

The limits on $z^{\prime }$ will occur where we find that $d{z}^{\prime }/d{y}^{\prime }=0$. We will figure out where, along the tilted ellipse, this happens by differentiating both sides of this last expression. First, note that,

$dB$	$=$	$[2b^2\sin \theta \cos \theta -2c^2\sin \theta \cos \theta ]d{z}^{\prime }=2\sin \theta \cos \theta (b^2-c^2)d{z}^{\prime },$
$dC$	$\equiv$	$b^2[2z_0\cos \theta +2(z^{\prime }){\cos }^{}\theta ]d{z}^{\prime }+2c^2{z}^{\prime }{\sin }^{}\theta d{z}^{\prime }$
	$\equiv$	$[2b^2{z}_0\cos \theta +2z^{\prime }(b^2{\cos }^{}\theta +c^2{\sin }^{}\theta )]d{z}^{\prime }.$

Hence,

$2Ad{y}^{\prime }$	$=$	$-dB\pm d[B^2-4AC{]}^{1/2}$
	$=$	$-dB\pm \frac{1}{2}[B^2-4AC{]}^{-1/2}[2B\cdot dB]\mp \frac{1}{2}[B^2-4AC{]}^{-1/2}[4A\cdot dC]$
$\Rightarrow 2A(B^2-4AC{)}^{1/2}d{y}^{\prime }$	$=$	$[\pm B-(B^2-4AC{)}^{1/2}]dB\mp 2AdC$
	$=$	$\left\{\right[\pm B-(B^2-4AC{)}^{1/2}]2\sin \theta \cos \theta (b^2-c^2)\mp 2A[2b^2{z}_0\cos \theta +2z^{\prime }(b^2{\cos }^{}\theta +c^2{\sin }^{}\theta )]\}d{z}^{\prime }.$

The derivative, $d{z}^{\prime }/d{y}^{\prime }$, will go to zero when the coefficient on the LHS goes to zero, that is, when,

$B^2$

$=$

$4AC.$

From the boxed-in derivation, above, we know that this occurs when,

$z^{\prime }$

$=$

$\pm ϵ(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}-z_0\cos \theta .$

And the corresponding value(s) of $y^{\prime }$ comes from the relation,

$y^{\prime }$	$=$	$\frac{B}{2A}\{-1\pm {\xcancel{[1-\frac{4AC}{B^2}{]}^{1/2}}}^0\}$
	$=$	$-\frac{b^2\sin \theta (z_0+z^{\prime }\cos \theta )-c^2{z}^{\prime }\sin \theta \cos \theta }{c^2{\cos }^2\theta +b^2{\sin }^2\theta }.$

A numerical evaluation for our sample problem gives:

$(z{\text{'}}_{\mathrm{m}\mathrm{i}\mathrm{n}},y^{\prime })$	$=$	$(-0.72369,-0.64380)$
$(z{\text{'}}_{\mathrm{m}\mathrm{a}\mathrm{x}},y^{\prime })$	$=$	$(+0.48246,+0.72697)$

Figure 3:   Tipped Y'-Z' plane(s) of Riemann Type I Ellipsoid file = Dropbox/3Dviewers/RiemannModels/RiemannCalculations.xlsx --- worksheet = Feb22tip
Blue ellipse (x/a = 0.0); Green ellipse (x/a = + 0.70)	Blue ellipse (x/a = 0.0); Green ellipse (x/a = - 0.85)

Lagrangian Trajectories in x'-y' Plane

Initial Determination

For a given choice of $z_0$, let's map out the Lagrangian trajectory in the x'-y' "equatorial" (i.e., z' = 0) plane. The y'(x') relation is,

$(y^{\prime }{)}_{z_0}$

$=$

$\left\{\frac{B}{2A}\right[-1\pm (1-\frac{4AC}{B^2}{)}^{1/2}]{\}}_{z^{\prime }=0},$

where,

$A_{z_0}=A$	$\equiv$	$c^2{\cos }^2\theta +b^2{\sin }^2\theta ,$
$B_{z_0}$	$=$	$[2b^2\sin \theta (z_0+z^{\prime }\cos \theta )-2c^2{z}^{\prime }\sin \theta \cos \theta {]}_{z^{\prime }=0}=2b^2\sin \theta (z_0),$
$C_{z_0}$	$=$	$[b^2(z_0+z^{\prime }\cos \theta {)}^2+c^2(z^{\prime }{)}^2{\sin }^{}\theta -b^2{c}^2{ϵ}^2{]}_{z^{\prime }=0}=b^2(z_0{)}^2-b^2{c}^2{ϵ}^2.$

That is to say,

$2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )(y^{\prime }{)}_{z_0}$	$=$	$-B_{z_0}\pm [B_{z_0}^2-4A{C}_{z_0}{]}^{1/2}$
	$=$	$-2z_0{b}^2\sin \theta \pm [4b^4{z}_0^2{\sin }^{}\theta -4(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )(b^2{z}_0^2-b^2{c}^2{ϵ}^2){]}^{1/2}$
$\Rightarrow (c^2{\cos }^2\theta +b^2{\sin }^2\theta )(y^{\prime }{)}_{z_0}$	$=$	$-z_0{b}^2\sin \theta \pm [(c^2{\cos }^{}\theta )(b^2{c}^2{ϵ}^2-b^2{z}_0^2)+(b^2{\sin }^{}\theta )(b^2{c}^2{ϵ}^2){]}^{1/2}$
	$=$	$-z_0{b}^2\sin \theta \pm bc[{ϵ}^2(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )-z_0^2{\cos }^{}\theta {]}^{1/2}.$

For a given choice of $z_0$, the limits on x' are given by when the argument of the square root is set to zero, that is,

${ϵ}^2$	$=$	$\frac{z_0^2{\cos }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}$
$\Rightarrow 1-(\frac{x^{\prime }}{a}{)}^2$	$=$	$\frac{z_0^2{\cos }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}$
$\Rightarrow \frac{x^{\prime }}{a}$	$=$	$\pm [1-\frac{z_0^2{\cos }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{]}^{1/2}.$

Various z_0 Slices

Are Orbits Exact Circles

After plotting $(y^{\prime }{)}_{z_0}$ as a function of $x^{\prime }$ (between the just-derived limits) for several different values of $z_0$, we noticed that each Lagrangian trajectory appears to be a circle. If this is exactly the case …

1.) RADIUS OF CIRCLE, MEASURED PERPENDICULAR TO x'-AXIS:   Given simply by this last expression, namely,

$[\frac{x^{\prime }}{a}{]}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$	$=$	$[1-\frac{z_0^2{\cos }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{]}^{1/2}$
$\Rightarrow (c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}[\frac{x^{\prime }}{a}{]}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$	$=$	$[(c^2{\cos }^2\theta +b^2{\sin }^2\theta )-z_0^2{\cos }^2\theta {]}^{1/2}$

2.) CENTER OF CIRCLE:   The y'-coordinate of the center of the circle is the value of $(y^{\prime }{)}_{z_0}$ obtained when the argument of the square root goes to zero. That is,

$(c^2{\cos }^2\theta +b^2{\sin }^2\theta )[(y^{\prime }{)}_{z_0}{]}_0$	$=$	$-z_0{b}^2\sin \theta \pm bc{\xcancel{[{ϵ}^2(c^2{\cos }^2\theta +b^2{\sin }^2\theta )-z_0^2{\cos }^2\theta {]}^{1/2}}}^0$
$\Rightarrow [(y^{\prime }{)}_{z_0}{]}_0$	$=$	$-\frac{z_0{b}^2\sin \theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}.$

And, along the $x^{\prime }$-axis, the inner and outer edges of the circle are identified by the positions at which $x^{\prime }/a=0\Rightarrow ϵ=1$. That is,

$(c^2{\cos }^2\theta +b^2{\sin }^2\theta )[(y^{\prime }{)}_{z_0}{]}_{\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{s}}$	$=$	$-z_0{b}^2\sin \theta \pm bc[{\xcancel{{ϵ}^2}}^1(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )-z_0^2{\cos }^{}\theta {]}^{1/2}$
$\Rightarrow [(y^{\prime }{)}_{z_0}{]}_{\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}\mathrm{s}}$	$=$	$-\{z_0{b}^2\sin \theta \mp bc[(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )-z_0^2{\cos }^{}\theta {]}^{1/2}\}(c^2{\cos }^{}\theta +b^2{\sin }^{}\theta {)}^{-1}.$

3.) RADIUS OF CIRCLE, MEASURED PERPENDICULAR TO x'-AXIS:   The radius of the "circle" along the $x^{\prime }$-axis is,

$[(y^{\prime }{)}_{z_0}{]}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$	$=$	$bc[(c^2{\cos }^2\theta +b^2{\sin }^2\theta )-z_0^2{\cos }^2\theta {]}^{1/2}(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{-1}$
$\Rightarrow (c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}[(y^{\prime }{)}_{z_0}{]}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$	$=$	$bc[1-\frac{z_0^2{\cos }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{]}^{1/2}.$

$\frac{z_0}{z_{\mathrm{m}\mathrm{a}\mathrm{x}}}$	$(x^{\prime }{)}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$	$(y^{\prime }{)}_0$	$(y^{\prime }{)}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$	$[\frac{y^{\prime }}{x^{\prime }}{]}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$
0.000	1.000	0.000	0.974797	0.974797
- 0.700	0.714143	- 0.625325	0.696144	0.974797
- 0.975	0.222205	- 0.870989	0.216605	0.974797

How do the two radii compare? As the (immediately above) table illustrates, each trajectory's x'-radius is slightly larger than that trajectory's y'-radius. Hence, the orbits are not circular! However, as the last column (bgcolor="yellow") tabulates, the degree of flattening is very slight and, surprisingly, the ratio of radii is identical in every case.

Let's examine the analytic expression for the ratio of radii:

$[\frac{x^{\prime }/a}{[(y^{\prime }{)}_{z_0}]}{]}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$	$=$	$[1-\frac{z_0^2{\cos }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{]}^{1/2}(bc{)}^{-1}[(c^2{\cos }^2\theta +b^2{\sin }^2\theta )-z_0^2{\cos }^2\theta {]}^{-1/2}(c^2{\cos }^2\theta +b^2{\sin }^2\theta )$
	$=$	$\frac{(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^{1/2}}{bc}.$

From this last expression, we see that the two radii will be the same — thereby making the LHS unity — only if,

$b^2{c}^2$	$=$	$c^2{\cos }^2\theta +b^2{\sin }^2\theta$
	$=$	$c^2{\cos }^2\theta +b^2(1-{\cos }^2\theta )$
$\Rightarrow b^2(c^2-1)$	$=$	$(c^2-b^2){\cos }^2\theta$
$\Rightarrow {\cos }^2\theta$	$=$	$\frac{b^2(c^2-1)}{(c^2-b^2)}=0.907244$
$\Rightarrow \theta$	$=$	$\pm 0.30948.$

This is not the case for our example model; its tilt angle is, instead, $\theta =-0.332029$.

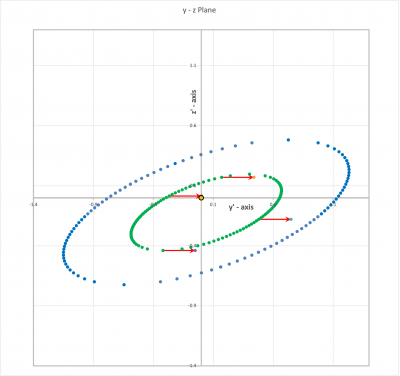
Plot Off-Center, Slightly Flattened Ellipse

$[\frac{y^{\prime }-y{\text{'}}_0}{y{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}}{]}^2$	$=$	$1-(\frac{x^{\prime }}{x{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}}{)}^2$
$\Rightarrow \frac{y^{\prime }-y{\text{'}}_0}{y{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}}$	$=$	$\pm [1-(\frac{x^{\prime }}{x{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}}{)}^2{]}^{1/2}$

This seems to work perfectly! We used Excel to generate trajectories using this expression and the results matched earlier determinations of these trajectories to machine precision.

Let's now examine the normal to the surface that is obtained from this compact trajectory expression. Given that $y{\text{'}}_0$, $y{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$, and $x{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}$ are all constants, we have,

$G^{\prime }$	$\equiv$	$[\frac{y^{\prime }-y{\text{'}}_0}{y{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}}{]}^2+(\frac{x^{\prime }}{x{\text{'}}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}}{)}^2-1$
$\frac{1}{2}\mathrm{\nabla }{G}^{\prime }$	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\frac{x^{\prime }}{(x^{\prime }{)}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{y^{\prime }-y{\text{'}}_0}{(y^{\prime }{)}_{\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{u}\mathrm{s}}^2}\right]$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\frac{x^{\prime }}{a^2}\right]\left[\frac{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}{(c^2-z_0^2){\cos }^2\theta +b^2{\sin }^2\theta }\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{y^{\prime }}{b^2{c}^2}\right]\left[\frac{(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^2}{(c^2-z_0^2){\cos }^2\theta +b^2{\sin }^2\theta }\right]-{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{y{\text{'}}_0}{b^2{c}^2}\right]\left[\frac{(c^2{\cos }^2\theta +b^2{\sin }^2\theta {)}^2}{(c^2-z_0^2){\cos }^2\theta +b^2{\sin }^2\theta }\right]$
$\Rightarrow \left[\frac{(c^2-z_0^2){\cos }^2\theta +b^2{\sin }^2\theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}\right]\frac{1}{2}\mathrm{\nabla }{G}^{\prime }$	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\frac{x^{\prime }}{a^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{y^{\prime }}{b^2{c}^2}\right][(c^2{\cos }^2\theta +b^2{\sin }^2\theta )]-{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{y{\text{'}}_0}{b^2{c}^2}\right][(c^2{\cos }^2\theta +b^2{\sin }^2\theta )]$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\frac{x^{\prime }}{a^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{y^{\prime }}{b^2{c}^2}\right][(c^2{\cos }^2\theta +b^2{\sin }^2\theta )]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{1}{b^2{c}^2}\right][z_0{b}^2\sin \theta ]$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\frac{x^{\prime }}{a^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{1}{b^2{c}^2}\right]\{y^{\prime }(c^2{\cos }^2\theta +b^2{\sin }^2\theta )+z_0{b}^2\sin \theta \}$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\frac{x^{\prime }}{a^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\{\frac{y^{\prime }{\cos }^2\theta }{b^2}+\frac{(y^{\prime }\sin \theta +z_0)\sin \theta }{c^2}\}.$

As we have already stated — but setting $z^{\prime }=0$ and ignoring the ${\hat{\mathbf{k}}}^{\prime }$ component because there is no motion in that direction —

$\frac{1}{2}\mathrm{\nabla }{P}^{\prime }(x^{\prime },y^{\prime },z^{\prime })$	$\to$	${\hat{\mathit{ı}}}^{\prime }\left(\frac{x^{\prime }}{a^2}\right)+{\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{(y^{\prime }\cos \theta -{\xcancel{z^{\prime }\sin \theta }}^0)\cos \theta }{b^2}]+[\frac{(z_0+{\xcancel{z^{\prime }\cos \theta }}^0+y^{\prime }\sin \theta )\sin \theta }{c^2}\left]\right\}+{\hat{\mathbf{k}}}^{\prime }{\xcancel{\{-[\frac{(y^{\prime }\cos \theta -z^{\prime }\sin \theta )\sin \theta }{b^2}]+[\frac{(z_0+z^{\prime }\cos \theta +y^{\prime }\sin \theta )\cos \theta }{c^2}\left]\right\}}}^0.$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left(\frac{x^{\prime }}{a^2}\right)+{\hat{\mathit{ȷ}}}^{\prime }\left\{\right[\frac{(y^{\prime }\cos \theta )\cos \theta }{b^2}]+[\frac{(z_0+y^{\prime }\sin \theta )\sin \theta }{c^2}\left]\right\}.$

Since, properly normalized, $\mathrm{\nabla }{G}^{\prime }$ is identical to $\mathrm{\nabla }{P}^{\prime }$, and since we have already shown that ${{\mathbf{𝐮}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$ is everywhere orthogonal to $\mathrm{\nabla }{P}^{\prime }$, it must be true that $\mathrm{\nabla }{G}^{\prime }$ is everywhere orthogonal to ${{\mathbf{𝐮}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$.

Hooray!!

See Also

• Description of Riemann Type I Ellipsoids
• Riemann Type 1 Ellipsoids (old introduction)
• Construction Challenges (Pt. 1)
• Construction Challenges (Pt. 2)
• Construction Challenges (Pt. 3)
• Construction Challenges (Pt. 4)
• Construction Challenges (Pt. 5)
• Construction Challenges (Pt. 6)

• Related discussions of models viewed from a rotating reference frame:
  • PGE
  • NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.