SSCpt1/Virial/FormFactors
Structural Form Factors
As has been defined in a companion, introductory discussion, three key dimensionless structural form factors are:
|
|
|
|
|
|
|
|
|
|
|
|
where, , and the subscript "0" denotes central values. The principal purpose of this chapter is to carry out the integrations that are required to obtain expressions for these structural form factors, at least in the few cases where they can be determined analytically. These form-factor expressions will then be used to provide expressions for the two constants, and , that appear in the free-energy function and in the virial theorem, and to provide corresponding expressions for the normalized energies, and .
Synopsis
|
Isolated Polytropes |
Pressure-Truncated Polytropes |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||||||||||
|
Isolated n = 1 Polytrope |
Pressure-Truncated n = 1 Polytropes |
||||||||||||||||||
|
|
||||||||||||||||||
|
Isolated n = 5 Polytrope |
Pressure-Truncated n = 5 Polytropes |
||||||||||||||||||
|
|
where, |
Expectation in Context of Pressure-Truncated Polytropes
For pressure-truncated polytropic configurations, the normalized virial theorem states that,
|
|
|
|
This provides one mechanism by which the correctness of our form-factor expressions can be checked. Specifically, having determined and from the derived form factors, we can see whether the sum of these energies as specified on the lefthand-side of this virial theorem expression indeed match the normalized energy term involving the external pressure, as specified on the righthand side. In order to facilitate this "reality check" at the end of each example, below, we will use Stahler's detailed force-balanced solution of the equilibrium structure of embedded polytropes to provide an expression for the term on the righthand side of the virial theorem expression.
We begin by plugging our general expression for into this righthand-side term and grouping factors to facilitate insertion of Stahler's expressions.
|
|
|
|
|
|
|
|
From Stahler's equilibrium solution, we have,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hence, the expectation based on Stahler's equilibrium models is that,
|
|
|
|
As a cross-check, multiplying this expression through by — where the expression for can be obtained from our discussions of detailed force-balanced models — gives a related result that can be obtained directly from Horedt's expressions, namely,
|
|
|
|
Viala and Horedt (1974) Expressions
Presentation
📚 Y. P. Viala & Gp. Horedt (1974, Astron. & Ap., Vol. 33, pp. 195 - 202) have provided analytic expressions for the gravitational potential energy and the internal energy — which they tag with the variable names, and , respectively — that we can adopt in our effort to quantify the key structural form factors in the context of pressure-truncated polytropic spheres. [The same expression for is also effectively provided in §1 of Horedt (1970) through the definition of his coefficient, "A" (polytropic case).]
|
Y. P. Viala & Gp. Horedt (1974)
| ||||||||||||
|
A couple of key equations drawn directly from 📚 Viala & Horedt (1974) have been shown here. As its title indicates, the paper includes discussion of — and accompanying equation derivations for — equilibrium self-gravitating, pressure-truncated, polytropic configurations having several different geometries: planar sheets, axisymmetric cylinders, and spheres. We have extracted derived expressions for the gravitational potential energy, , and the internal energy, , that apply to spherically symmetric configurations only. These authors also consider negative polytropic indexes; we are considering only values in the range, , so, as the accompanying parenthetical note indicates, when either or appears in an expression, we will pay attention only to the superior sign. |
||||||||||||
Rewriting these two expressions to accommodate our parameter notations — recognizing, specifically, that is the familiar polytropic length scale (; expression provided below), is the central density , and — we have from 📚 Viala & Horedt (1974),
|
|
|
|
|
|
|
|
First Reality Check
As a quick reality check, let's see whether, when appropriately added together, these two energies satisfy the scalar virial theorem for isolated polytropes.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For isolated polytropes, , so this sum of terms goes to zero, as it should if the system is in virial equilibrium.
Renormalization
Both of the energy-term expressions derived by 📚 Viala & Horedt (1974) are written in terms of and
|
|
|
|
— that is, effectively in terms of and — whereas, in the context of our discussions, we would prefer to express them in terms of our generally adopted energy normalization,
|
|
|
|
In order to accomplish this, we need to replace the central density with the total mass of an isolated polytrope, , whose generic expression is (see, for example, equation 69 of Chandrasekhar),
|
|
|
|
Hence, we have,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
So, employing our preferred normalization, the 📚 Viala & Horedt (1974) expressions become,
|
|
|
|
|
|
|
|
Second Reality Check
If we now renormalize the sum of energy terms discussed in our first reality check, above, we have,
|
|
|
|
(This may or may not be useful!)
Implication for Structural Form Factors
On the other hand, our expressions for these two normalized energy components written in terms of the structural form factors are,
|
|
|
|
|
|
|
|
where, in equilibrium (see here and here for details),
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hence, we deduce that,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If we now adopt the VH74 expression for the normalized gravitational potential energy, the product of terms inside the curly braces becomes,
|
|
|
|
|
|
|
|
Therefore,
|
|
|
|
|
|
|
|
Now, from our earlier work we deduced that is related to via the relation,
|
|
|
|
Hence, we now have,
|
|
|
|
|
|
|
|
Building on the work of VH74, we have, quite generally,
|
Structural Form Factors for Isolated Polytropes |
Structural Form Factors for Pressure-Truncated Polytropes |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
||||||||||||||||||
|
We should point out that 📚 D. Lai, F. A. Rasio, & S. L. Shapiro (1993b, ApJ Suppl., Vol. 88, pp. 205 - 252) define a different set of dimensionless structure factors for isolated polytropic spheres — (their equation 2.9) is used in the determination of the internal energy; and (their equation 2.10) is used in the determination of the gravitational potential energy.
Note that these are defined in the context of energy expressions wherein the central density, rather than the configuration's radius, serves as the principal parameter. We note, as well, that for rotating configurations they define two additional dimensionless structure factors — (their equation 3.17) is used in the determination of the rotational kinetic energy; and (their equation 3.14; also equation 7.4.9 of [ST83]) is used in the determination of the moment of inertia. |
|||||||||||||||||||
The singularity that arises when leads us to suspect that these general expressions fail in that one specific case. Fortunately, as we have shown in an accompanying discussion, and , as well as , can be determined by direct integration in this single case.
Related Discussions
First Detailed Example (n = 5)
Here we complete these integrals to derive detailed expressions for the above subset of structural form factors in the case of spherically symmetric configurations that obey an polytropic equation of state. The hope is that this will illustrate, in a clear and helpful manner, how the task of calculating form factors is to be carried out, in practice; and, in particular, to provide one nontrivial example for which analytic expressions are derivable. This should simplify the task of debugging numerical algorithms that are designed to calculate structural form factors for more general cases that cannot be derived analytically. The limits of integration will be specified in a general enough fashion that the resulting expressions can be applied, not only to the structures of isolated polytropes, but to pressure-truncated polytropes that are embedded in a hot, tenuous external medium and to the cores of bipolytropes.
Foundation (n = 5)
We use the following normalizations, as drawn from our more general introductory discussion:
|
Adopted Normalizations | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||
|
Note that the following relations also hold:
| |||||||||||||||||||
As is detailed in our accompanying discussion of bipolytropes — see also our discussion of the properties of isolated polytropes — in terms of the dimensionless Lane-Emden coordinate, , where,
the radial profile of various physical variables is as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Notice that, in these expressions, the central density, , has been used instead of to normalize the relevant physical variables. We can switch from one normalization to the other by realizing that — see, again, our accompanying discussion — in isolated polytropes, the total mass is given by the expression,
Employing this mapping to switch to our "preferred" adopted normalizations, as defined in the above boxed-in table, the four radial profiles become,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mass1 (n = 5)
While we already know the expression for the profile, having copied it from our discussion of detailed force-balanced models of isolated polytropes, let's show how that profile can be derived by integrating over the density profile. After employing the norm-subscripted quantities, as defined above, to normalize the radial coordinate and the mass density in our introductory discussion of the virial theorem, we obtained the following integral defining the,
Normalized Mass:
|
|
|
|
Plugging in the profiles for and , and recognizing that,
gives, with the help of Mathematica's Online Integrator,

|
|
|
|
|
|
|
|
|
|
|
|
As it should, this expression exactly matches the normalized profile shown above. Notice that if we decide to truncate an polytrope at some radius, — as in the discussion that follows — the mass of this truncated configuration will be, simply,
|
|
|
|
Mass2 (n = 5)
Alternatively, as has been laid out in our accompanying summary of normalized expressions that are relevant to free-energy calculations,
|
|
|
|
where, is the "total" mass of the polytropic configuration that is truncated at ; keep in mind that, here,
is the total mass of the isolated polytrope, that is, a polytrope whose Lane-Emden radius extends all the way to . In our discussions of truncated polytropes, we often will use to specify the truncated radius in terms of the familiar, dimensionless Lane-Emden radial coordinate, so here we will set,
Hence, in terms of the desired integration coordinate, , the density profile provided above becomes,
|
and the integral defining becomes,
|
|
|
|
|
|
|
|
In this case, integrating "all the way out to the surface" means setting and, hence, ; by definition, it also means . Therefore we have,
|
|
|
|
|
|
|
|
Using this expression for the mean-to-central density ratio along with the expression for the ratio, , derived in the preceding subsection, we also can state that for truncated polytropes,
|
|
|
|
|
|
|
|
By making the substitution, , this expression becomes identical to the profile presented just before the "Mass1" subsection, above. In summary, then, we have the following two equally valid expressions for the profile — one expressed as a function of and the other expressed as a function of :
|
Mean-to-Central Density (n = 5)
From the above line of reasoning we appreciate that, for any spherically symmetric configuration, the ratio of the configuration's mean density to its central density can be obtained by setting the upper limit of our just-completed "Mass2" integration to . That is to say, quite generally,
|
|
|
|
|
|
|
|
But the integral expression on the righthand side of this relation is also the definition of the structural form factor, , given at the top of this page. Hence, we can say, quite generally, that,
And, given that we have just completed this integral for the case of truncated polytropic structures, we can state, specifically, that,
Gravitational Potential Energy (n = 5)
As presented at the top of this page, the structural form factor associated with determination of the gravitational potential energy is,
|
|
|
|
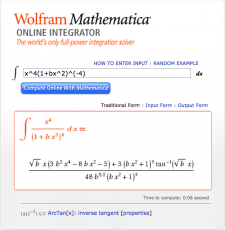
Given that an expression for the normalized density profile,
, has already been determined, above, we can carry out the nested pair of integrals immediately. Indeed, the integral contained inside of the curly braces has already been completed in the "Mass2" subsection, above, in order to determine the radial mass profile. Specifically, we have already determined that,
|
|
|
|
|
|
|
|
Hence, with the help of Mathematica's Online Integrator, we have,
|
|
|
|
|
|
|
|
|
|
|
|
|
ASIDE: Now that we have expressions for, both, and , we can determine an analytic expression for the normalized gravitational potential energy for truncated, polytropes. As is shown in a companion discussion,
where,
In order to simplify typing, we will switch to the variable,
in which case a summary of derived expressions, from above, gives,
Hence,
This exactly matches the normalized gravitational potential energy derived independently in the context of our exploration of bipolytropes, referred to in that discussion as . Hence, also, as defined in the accompanying introductory discussion, the constant, , that appears in our general free-energy equation is (for polytropic configurations),
|
Thermal Energy (n = 5)
As presented at the top of this page, the structural form factor associated with determination of the configuration's thermal energy is,
|
|
|
|
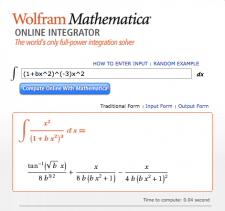
Given that an expression for the normalized pressure profile,
, has already been provided, above, we can carry out the integral immediately. Specifically, we have,
|
|
|
|
|
|
|
|
Hence, with the aid of Mathematica's Online Integrator, the relevant integral gives,
|
|
|
|
|
|
|
|
|
ASIDE: Having this expression for allows us to determine an analytic expression for the coefficient, , that appears in our general expression for the free energy, and that can be straightforwardly used to obtain an expression for the thermal energy content of polytropic configurations. From our accompanying introductory discussion, we have,
If, as above, we adopt the simplifying variable notation,
the various factors in the definition of and are (see above),
Hence,
This exactly matches the normalized thermal energy derived independently in the context of our exploration of bipolytropes, referred to in that discussion as . Its similarity to the expression for the gravitational potential energy — which is relevant to the virial theorem — is more apparent if it is rewritten in the following form:
|
Summary (n = 5)
In summary, for structures we have,
|
Structural Form Factors (n = 5) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |||||||||
|
Free-Energy Coefficients (n = 5) | |||||||||
| |||||||||
|
Normalized Energies (n = 5) | |||||||||
|
Reality Check (n = 5)
|
|
|
|
|
|
|
|
|
|
|
|
For embedded polytropes, this should be compared against the expectation (prediction) provided by Stahler's equilibrium models, as detailed above. Given that, for polytropes — see the "Mass1" discussion above and our accompanying tabular summary of relevant properties,
|
|
; |
|
and |
|
the expectation is that,
|
|
|
|
|
|
|
|
|
|
|
|
This precisely matches our sum of the thermal and gravitational potential energies, as just determined using our expressions for the structural form factors. This gives us confidence that our form-factor expressions are correct, at least in the case of embedded polytropic structures.
Second Detailed Example (n = 1)
Foundation (n = 1)
We use the following normalizations, as drawn from our more general introductory discussion:
|
Adopted Normalizations | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||
|
Note that the following relations also hold:
| |||||||||||||||||||
As is detailed in our discussion of the properties of isolated polytropes, in terms of the dimensionless Lane-Emden coordinate, , where,
the radial profile of various physical variables is as follows:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Notice that, in these expressions, the central density, , has been used instead of to normalize the relevant physical variables. We can switch from one normalization to the other by realizing that — see, again, our accompanying discussion — in isolated polytropes, the total mass is given by the expression,
Employing this mapping to switch to our "preferred" adopted normalizations, as defined in the above boxed-in table, the four radial profiles become,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mass1 (n = 1)
While we already know the expression for the profile, having copied it from our discussion of detailed force-balanced models of isolated polytropes, let's show how that profile can be derived by integrating over the density profile. After employing the norm-subscripted quantities, as defined above, to normalize the radial coordinate and the mass density in our introductory discussion of the virial theorem, we obtained the following integral defining the,
Normalized Mass:
|
|
|
|
Plugging in the profiles for and gives, with the help of Mathematica's Online Integrator,
|
|
|
|
|
|
|
|
|
|
|
|
As it should, this expression exactly matches the normalized profile shown above. Notice that if we decide to truncate an polytrope at some radius, — as in the discussion that follows — the mass of this truncated configuration will be, simply,
|
|
|
|
Mass2 (n = 1)
Alternatively, as has been laid out in our accompanying summary of normalized expressions that are relevant to free-energy calculations,
|
|
|
|
where, is the "total" mass of the polytropic configuration that is truncated at ; keep in mind that, here,
is the total mass of the isolated polytrope, that is, a polytrope whose Lane-Emden radius extends all the way to . In our discussions of truncated polytropes, we often will use to specify the truncated radius in terms of the familiar, dimensionless Lane-Emden radial coordinate, so here we will set,
Hence, in terms of the desired integration coordinate, , the density profile provided above becomes,
|
and the integral defining becomes,
|
|
|
|
|
|
|
|
In this case, integrating "all the way out to the surface" means setting and, hence, ; by definition, it also means . Therefore we have,
|
|
|
|
|
|
|
|
Using this expression for the mean-to-central density ratio along with the expression for the ratio, , derived in the preceding subsection, we also can state that for truncated polytropes,
|
|
|
|
|
|
|
|
By making the substitution, , this expression becomes identical to the profile presented just before the "Mass1" subsection, above. In summary, then, we have the following two equally valid expressions for the profile — one expressed as a function of and the other expressed as a function of :
|
Mean-to-Central Density (n = 1)
Following the line of reasoning provided above, we can use the just-derived central-to-mean density ratio to specify one of the structural form factors. Specifically,
Gravitational Potential Energy (n = 1)
As presented at the top of this page, the structural form factor associated with determination of the gravitational potential energy is,
|
|
|
|
From the derivations already presented, above, for polytropic configurations, we know all of the functions under this integral. We know, for example, that,
|
|
|
|
Hence, with the help of Mathematica's Online Integrator, we have,
|
|
|
|
|
|
|
|
|
|
|
|
|
ASIDE: Now that we have expressions for, both, and , we can determine an analytic expression for the normalized gravitational potential energy for truncated, polytropes. As is shown in a companion discussion,
where,
A summary of derived expressions, from above, gives,
Hence,
|
Thermal Energy (n = 1)
As presented at the top of this page, the structural form factor associated with determination of the configuration's thermal energy is,
|
|
|
|
Given that an expression for the normalized pressure profile, , has already been provided, above, we can carry out the integral immediately. Specifically, we have,
|
|
|
|
|
|
|
|
Hence, with the aid of Mathematica's Online Integrator, the relevant integral gives,
|
|
|
|
|
|
|
|
|
ASIDE: Having this expression for allows us to determine an analytic expression for the coefficient, , that appears in our general expression for the free energy, and that can be straightforwardly used to obtain an expression for the thermal energy content of polytropic configurations. From our accompanying introductory discussion, we have,
The various factors in the definition of and are (see above),
Hence,
|
Summary (n = 1)
In summary, for structures we have,
|
Structural Form Factors (n = 1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |||||||||
|
Free-Energy Coefficients (n = 1) | |||||||||
| |||||||||
|
Normalized Energies (n = 1) | |||||||||
|
Reality Checks (n = 1)
Expectation from Stahler's Equilibrium Models
If we add twice the thermal energy to the gravitational potential energy, we obtain,
|
|
|
|
|
|
|
|
For embedded polytropes, this should be compared against the expectation (prediction) provided by Stahler's equilibrium models, as detailed above. Given that, for polytropes — see the "Mass1" discussion above and our accompanying tabular summary of relevant properties,
|
|
; |
|
and |
|
the expectation is that,
|
|
|
|
|
|
|
|
|
|
|
|
This precisely matches our sum of the thermal and gravitational potential energies, as just determined using our expressions for the structural form factors, giving us additional confidence that our form-factor expressions are correct.
Compare With General Expressions Based on VH74 Work
Based on the general expressions derived above in the context of VH74, for the specific case of polytropic configurations, the three structural form factor should be,
|
|
|
|
|
|
|
|
|
|
|
|
Also, remember that,
|
|
|
|
|
|
|
|
|
|
|
|
Now, let's look at the structural form factors, one at a time. First, we have,
|
|
|
|
which matches the expression presented in the summary table, above. Next,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
which also matches the expression presented in the summary table, above. Finally,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
which also matches the expression presented in the summary table, above. So this adds support to the deduction, above, that VH74 have provided us with the information necessary to develop general expressions for the three structural form factors.
Fiddling Around
NOTE (from Tohline on 17 March 2015): Chronologically, this "Fiddling Around" subsection was developed before our discovery of the VH74 derivations. It put us on track toward the correct development of general expressions for the structural form factors that are applicable to pressure-truncated polytropic spheres. But this subsection's conclusions are superseded by the VH74 work.
In this subsection, for simplicity, we will omit the "tilde" over the variable . In the case of structures,
|
|
|
|
|
|
|
|
|
|
|
|
But, we also have shown that,
|
|
|
|
Hence, we see that,
|
|
|
|
Similarly, in the case of structures,
|
|
|
|
|
|
|
|
|
|
|
|
But, we also have shown that,
|
|
|
|
Hence, we see that,
|
|
|
|
|
|
|
|
This is pretty amazing! Both examples produce almost exactly the same relationship between the two structural form factors, and . I think that we are well on our way toward nailing down the generic, analytic relationship and, in turn, a generally applicable mass-radius relationship for pressure-truncated polytropic configurations.
Okay … here is the final piece of information. In the case of isolated polytropes, we know that the correct expressions for the structural form factors are as summarized in the following table:
|
Structural Form Factors for Isolated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
We notice, from this, that the ratio,
|
|
|
|
|
|
|
|
Even in the case of the two pressure-truncated polytropes, analyzed above, this ratio proves to give the correct prefactor on . So we suspect that the universal relationship between the two form factors is,
|
|
|
|
See Also
- Index to a Variety of Free-Energy and/or Virial Analyses
- Spherically Symmetric Configurations (SSC) Index

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |