Apps/MaclaurinToroid
Overview
|
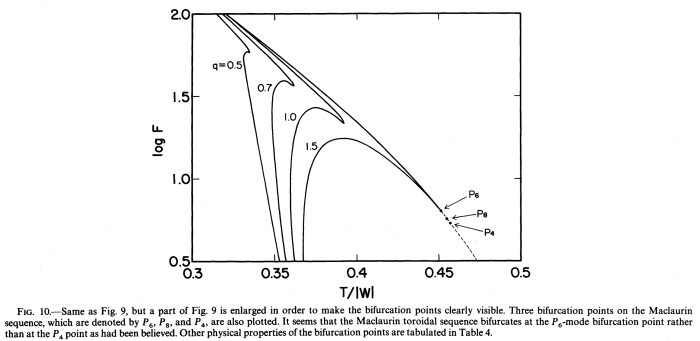
"It has been previously stated in the literature that the Maclaurin toroid sequence bifurcates from the Maclaurin spheroidal sequence at the bifurcation point (📚 Y. Eriguchi & I. Hachisu (1985, A&A, Vol. 148, pp. 289 - 292), … Since the bifurcation point occurs along the spheroidal sequence at … this is synonymous with saying that Maclaurin spheroids that have are dynamically stable against linear, axisymmetric perturbations. This conclusion is based, in large part, on the fact that the linear perturbation analysis performed by 📚 J. M. Bardeen (1971, ApJ, Vol. 167, pp. 425 - 446)… found that the ring mode instability against a mode perturbation sets in at exactly the bifurcation point." "📚 Bardeen (1971), however, did not examine the behavior of axisymmetric modes higher than 📚 Eriguchi & Hachisu (1985) have tabulated bifurcation points along the Maclaurin spheroidal sequence for a number of axisymmetric modes higher than and have found the point that occurs at the lowest value of on the sequence to be the and not at the bifurcation point. We suspect, therefore that when a general linear perturbation analysis is performed, the first dynamical axisymmetric (ring) mode instability will be found to set in at and that the unstable mode will be of a geometric form." |
|
— Drawn from (p. 598 of) 📚 I. Hachisu, J. E. Tohline, & Y. Eriguchi (1987, ApJ, Vol. 323, pp. 592 - 613) |
|
Figure 10 extracted from p. 602 of |
|||||||||
|
NOTE:
|
|||||||||
Maclaurin Toroid (MPT77)
| Maclaurin Toroid Sequence MPT77 |
|---|
In a separate chapter, we focused on the pioneering work of 📚 F. W. Dyson (1893, Phil. Trans. Royal Soc. London. A., Vol. 184, pp. 43 - 95), 📚 F. W. Dyson (1893, Phil. Trans. Royal Soc. London. A., Vol. 184, pp. 1041 - 1106) and, more recently, 📚 C. -Y. Wong (1974, ApJ, Vol. 190, pp. 675 - 694), who determined the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. We will refer to these uniformly rotating configurations as "Dyson-Wong tori."
Here, we summarize the work of 📚 P. S. Marcus, W. H. Press, & S. A. Teukolsky (1977, ApJ, Vol. 214, pp. 584 - 597) — hereafter, MPT77 — who constructed a sequence of toroidal-shaped, self-gravitating, incompressible configurations that are not uniformly rotating but, rather, have a distribution of angular momentum that is identical to the distribution found in a uniformly rotating, uniform-density sphere. As we have pointed out in our associated overview of "simple rotation curves", this chosen (cylindrical) radial distribution of specific angular momentum is given by the expression,
|
|
|
|
|
📚 Stoeckly (1965), §II.c, Eq. (12) |
||
where, is the total angular momentum, is the total mass, the mass fraction,
and is the mass enclosed within a cylinder of radius, . Such equilibrium models are often referred to as configurations, although MPT77 do not use this terminology. Following the lead of MPT77, we will refer to each of their equilibrium configurations as a "Maclaurin Toroid."
Maclaurin Spheroid Reminder
As has been demonstrated in our accompanying discussion of the Maclaurin spheroid sequence, the (square of the) normalized angular momentum that is associated with a spheroid of eccentricity, , is,
|
|
|
|
|
📚 Marcus, Press, & Teukolsky (1977), §IVa, p. 591, Eq. (4.2) |
||
In that same discussion, we have demonstrated that the corresponding ratio of rotational to gravitational potential energy is given by the expression,
|
|
|
|
|
📚 Marcus, Press, & Teukolsky (1977), §IVc, p. 594, Eq. (4.4) |
||
Figure 4 from this accompanying discussion shows how varies with along the Maclaurin Spheroid sequence. In an effort to conform to MPT77's presentation, our Figure 1 (immediately below) displays the same information as displayed in Figure 4 of this separate chapter, but the axes have been swapped and the maximum displayed value of has been extended from 1 to 1.5.
| |||||
MPT77 also evaluate the normalized total energy, , of each of their constructed equilibrium configurations, where
|
|
|
|
and, according to the caption of their Figure 4, is "… the energy of a nonrotating sphere of equal mass and volume." Drawing from our separate discussion of the Maclaurin spheroid sequence, it would be reasonable to assume that the energy normalization adopted by MPT77 is the same as the normalization used by [T78], namely,
|
|
|
|
For models along the Maclaurin spheroid sequence, this normalization leads to expressions for the two key energy terms of the form,
|
|
|
|
|
|
|
|
in which case, in the limit of a nonrotating sphere,
|
|
|
|
But in Figure 4 of MPT77, the point along the Maclaurin spheroid sequence — the solid, black curve — that represents a nonrotating sphere has a normalized energy, We conclude, therefore, that the normalization adopted by MPT77 is,
|
|
|
|
Our Figure 2 (immediately above) attempts to quantitatively replicate the behavior of the Maclaurin spheroid sequence that is shown in Figure 4 (p. 213) of MPT77; the ordinate depicts, on a base-10 logarithmic scale, how the total energy varies with the spheroid's angular momentum over the range, . More specifically, for eccentricities over the range, , the corresponding value of the spheroid's normalized angular momentum is obtained from the above expression for , and the normalized energy is given by the relation,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Constructed Maclaurin Toroid Models
📚 Marcus, Press, & Teukolsky (1977) did not create a tabulated description of the models that they constructed along their so-called "Maclaurin Toroid" sequence. Throughout their paper, however, they highlighted some properties of a selected group of equilibrium models. Column (2) of Table 1, immediately below, provides a list of the values of the normalized angular momentum, , that corresponds to the Maclaurin Toroid models that have been explicitly referenced in their discussion.
| Table 1 | |||||
| Model | Spheroid Equivalent | Notes … | |||
| (1) | (2) | (3) | (4) | (5) | |
| (a) | |||||
| (b) | |||||
| (c) | |||||
| (d) | |||||
| (e) | |||||
|
Notes:
|
|||||
Using a simple iterative technique, we have determined the value of that corresponds to each tabulated if we assume that the referenced model is a Maclaurin spheroid, not a toroid; the value that corresponds to each spheroid's eccentricity is listed in column (3) of the table. In turn, columns (4) and (5) list the values of and that is associated with a Maclaurin spheroid that has the stated eccentricity. If — using the coordinate pair, — we were to position any one of these models into our Figure 1, above, the model would fall on the solid black portion of the "Maclaurin spheroid sequence." Similarly, if — using the coordinate pair, — we were to position any one of these models into our Figure 2, above, the model would fall on the solid black portion of the "Maclaurin spheroid sequence."
| Table 2 Data extracted via pencil & ruler measurement from Figs. 4 and 5 of … P. S. Marcus, W. H. Press, & S. A. Teukolsky (1977) Stablest Shapes for an Axisymmetric Body of Gravitating, Incompressible Fluid The Astrophysical Journal, Vol. 214, pp. 584 - 597 |
|||||
| Model | "Measured" Spheroid Properties | "Measured" Toroid Properties | |||
| (1) | (2) | (3) | (4) | (5) | (6) |
| --- | --- | ||||
| --- | |||||
| --- | |||||
|
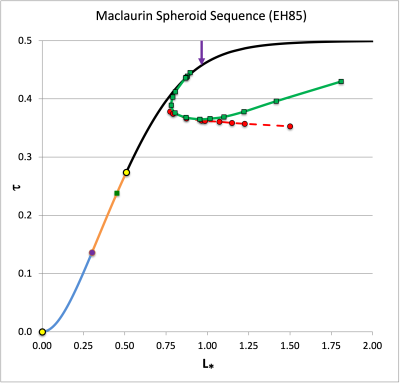
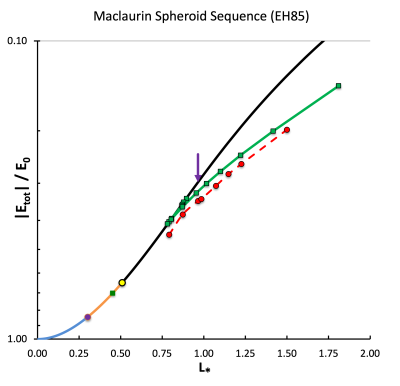
Maclaurin Toroid (EH85)
📚 Y. Eriguchi & I. Hachisu (1985, A&A, Vol. 148, pp. 289 - 292) — hereafter, EH85 — have constructed a set of uniform-density, axisymmetric configurations that show how the Maclaurin toroid sequence is connected to the Maclaurin spheroid sequence. The following table displays the structural characteristics of these configurations; the numbers in the first four columns have been drawn directly from Table 1 of EH85. The quantity, , that has been used to normalize the total energy in, for example, the fourth column of this table, is given by the expression,
|
📚 Eriguchi & Hachisu (1985), §2.2, p. 291, Eq. (7) |
||
For purposes of comparison between the separate published works of MPT77 and EH85, here we desire to shift back to the normalization adopted by MPT77, namely,
|
|
|
|
Building on our separate discussion of energy normalizations where we showed that,
|
|
|
|
we recognize immediately that,
|
|
|
|
We have evaluated this conversion factor and the consequential normalized total energy for each of the EH85 equilibrium configurations and have presented the results in columns six and seven, respectively, of the following table.
|
Data extracted from Table 1 (p. 290) of … |
Our Determination |
|||||
|
|
Relationship with the Dyson-Wong One-Ring Sequence
📚 D. M. Christodoulou, D. Kazanas, I. Shlosman, & J. E. Tohline (1995b, ApJ, Vol. 446, pp. 485 - 499) discuss how to interpret the physical meaning of the Maclaurin Toroid sequence, especially in the context of its relationship to the Maclaurin spheroid sequence and to the Dyson-Wong one-ring sequence. In this discussion, reference is made to the work of 📚 I. Hachisu, J. E. Tohline, & Y. Eriguchi (1987, ApJ, Vol. 323, pp. 592 - 613).
See Also

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |