ThreeDimensionalConfigurations/ChallengesPt4

Challenges Constructing Ellipsoidal-Like Configurations (Pt. 4)

This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1), (Pt. 2), and (Pt. 3). The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames.

The Plan

Intersection Expression

STEP #1

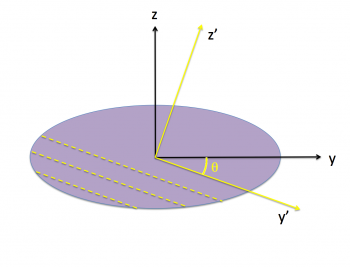
First, we present the mathematical expression that describes the intersection between the surface of an ellipsoid and a plane having the following properties:

• The plane cuts through the ellipsoid's z-axis at a distance, $z_0$, from the center of the ellipsoid;
• The line of intersection is parallel to the x-axis of the ellipsoid; and,
• The line that is perpendicular to the plane and passes through the z-axis at $z_0$ is tipped at an angle, $\theta$, to the z-axis.

As is illustrated in Figure 1, we will use the line referenced in this third property description to serve as the z'-axis of a Cartesian grid that is tipped at the angle, $\theta$, with respect to the body frame; and we will align the x' axis with the x-axis, so it should be clear that the z'-axis lies in the y-z plane of the ellipsoid.

Figure 1
$x$ $=$ $x^{\prime },$ $y$ $=$ $y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$ $(z-z_0)$ $=$ $z^{\prime }\cos \theta +y^{\prime }\sin \theta .$		$x^{\prime }$ $=$ $x,$ $y^{\prime }$ $=$ $y\cos \theta +(z-z_0)\sin \theta ,$ $z^{\prime }$ $=$ $(z-z_0)\cos \theta -y\sin \theta .$

As has been shown in our accompanying discussion, we obtain the following,

Intersection Expression
$1-\frac{x^2}{a^2}$	$=$	$y^2\left[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}\right]+y\left[\frac{2z_0\tan \theta }{c^2}\right]+\frac{z_0^2}{c^2},$

as long as z₀ lies within the range,

$z_0^2$

$\le$

$c^2+b^2{\tan }^2\theta .$

Rewriting this "intersection expression" in terms of the tipped (primed) coordinate frame gives us,

$1-\frac{(x^{\prime }{)}^2}{a^2}$

$=$

$(y^{\prime }\cos \theta -z^{\prime }\sin \theta {)}^2[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}]+(y^{\prime }\cos \theta -z^{\prime }\sin \theta )[\frac{2z_0\tan \theta }{c^2}]+\frac{z_0^2}{c^2}.$

STEP #2

As viewed from the tipped coordinated frame, the curve that is identified by this intersection should be an

Off-Center Ellipse
$1$	$=$	$[\frac{x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2+[\frac{y^{\prime }-y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2$
	$=$	$[\frac{x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2+[\frac{(y^{\prime }{)}^2-2y^{\prime }{y}_c+y_c^2}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}],$

that lies in the x'-y' plane — that is, $z^{\prime }=0$. Let's see if the intersection expression can be molded into this form.

$1-\frac{z_0^2}{c^2}-\frac{(x^{\prime }{)}^2}{a^2}$	$=$	$(y^{\prime }{)}^2[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}]{\cos }^2\theta +2y^{\prime }[\frac{z_0\sin \theta }{c^2}]$
	$=$	$\left[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}\right]{\cos }^2\theta \{(y^{\prime }{)}^2-2y^{\prime }\left[\frac{-z_0\sin \theta }{c^2{\cos }^2\theta }\right]\left[\frac{b^2{c}^2}{c^2+b^2{\tan }^2\theta }\right]\}$
	$=$	${\kappa }^2[(y^{\prime }{)}^2-2y^{\prime }\underset{y_c}{\underbrace{\left(\frac{-z_0\sin \theta }{c^2{\kappa }^2}\right)}}],$

RESULT 3 (same as Result 1, but different from Result 2, below)

$\frac{y_c}{z_0}$ $=$ $-\frac{\sin \theta }{c^2{\kappa }^2}$

where,

${\kappa }^2$

$\equiv$

$\frac{c^2{\cos }^2\theta +b^2{\sin }^2\theta }{b^2{c}^2}.$

Dividing through by ${\kappa }^2$, then adding $y_c^2$ to both sides gives,

$(y^{\prime }{)}^2-2y^{\prime }{y}_c+y_c^2$

$=$

$\underset{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{\underbrace{[\frac{1}{{\kappa }^2}-\frac{z_0^2}{c^2{\kappa }^2}+y_c^2]}}-\frac{(x^{\prime }{)}^2}{a^2{\kappa }^2}.$

Finally, we have,

$\frac{1}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}[(y^{\prime }{)}^2-2y^{\prime }{y}_c+y_c^2]$

$=$

$1-(x^{\prime }{)}^2\underset{1/x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{\underbrace{\left[\frac{1}{a^2{\kappa }^2{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]}}.$

So … the intersection expression can be molded into the form of an off-center ellipse if we make the following associations:

$\frac{y_c}{z_0}$ $=$ $-\frac{\sin \theta }{c^2{\kappa }^2},$ $y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ $=$ $\frac{1}{{\kappa }^2}[1-\frac{z_0^2}{c^2}-\frac{z_0\sin \theta }{c^2}],$ $x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ $=$ $a^2[1-\frac{z_0^2}{c^2}-\frac{z_0\sin \theta }{c^2}].$ Note as well that, $(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2$ $=$ $a^2{\kappa }^2=\frac{a^2}{b^2{c}^2}[c^2{\cos }^2\theta +b^2{\sin }^2\theta ].$

Lagrangian Trajectory and Velocities

We presume that the off-center ellipse that is defined by the intersection expression identifies the trajectory of a Lagrangian fluid element. If this is the case, there are a couple of ways that the velocity — both the amplitude and its vector orientation — can be derived.

STEP #3

If the intersection expression identifies a Lagrangian trajectory, then the velocity vector must be tangent to the off-center ellipse at every location. At each $(x^{\prime },y^{\prime })$ coordinate location, the slope of the above-defined off-center ellipse is,

$\frac{d{y}^{\prime }}{d{x}^{\prime }}$

$=$

$(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2\frac{x^{\prime }}{(y_c-y^{\prime })}.$

From this expression we deduce that the x'- and y'- components of the velocity vector are, respectively,

$\frac{{\hat{\mathit{ı}}}^{\prime }\cdot {\mathit{u}}^{\prime }}{[{\mathit{u}}^{\prime }\cdot {\mathit{u}}^{\prime }{]}^{1/2}}$

$=$

$\frac{1}{u{\text{'}}_0}\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)(y_c-y^{\prime }),$

and,

$\frac{{\hat{\mathit{ȷ}}}^{\prime }\cdot {\mathit{u}}^{\prime }}{[{\mathit{u}}^{\prime }\cdot {\mathit{u}}^{\prime }{]}^{1/2}}$

$=$

$\frac{1}{u{\text{'}}_0}\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)x^{\prime },$

where the position-dependent — and, hence also, the time-dependent — length scale,

$u{\text{'}}_0$	$\equiv$	$\left\{\right[\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)(y_c-y^{\prime }){]}^2+\left[\frac{1}{|u^{\prime }|}\right(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}})x^{\prime }{]}^2{\}}^{1/2}$
	$=$	$\frac{1}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}}[x_{\mathrm{m}\mathrm{a}\mathrm{x}}^4(y_c-y^{\prime }{)}^2+y_{\mathrm{m}\mathrm{a}\mathrm{x}}^4(x^{\prime }{)}^2{]}^{1/2}.$

STEP #4

As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,

$x^{\prime }$	$=$	$x_{\mathrm{m}\mathrm{a}\mathrm{x}}\cos (\dot{\phi }t)$	and,	$y^{\prime }-y_c$	$=$	$y_{\mathrm{m}\mathrm{a}\mathrm{x}}\sin (\dot{\phi }t),$
${\dot{x}}^{\prime }$	$=$	$-x_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }\cdot \sin (\dot{\phi }t)=(y_c-y^{\prime })\left[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }$	and,	${\dot{y}}^{\prime }$	$=$	$y_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }\cdot \cos (\dot{\phi }t)=x^{\prime }\left[\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }.$

This means that the (dimensional) velocity vector is,

${\mathit{u}}^{\prime }$	$=$	${\hat{\mathit{ı}}}^{\prime }{\dot{x}}^{\prime }+{\hat{\mathit{ȷ}}}^{\prime }{\dot{y}}^{\prime }$
	$=$	${\hat{\mathit{ı}}}^{\prime }[(y_c-y^{\prime })(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left)\dot{\phi }\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[x^{\prime }\right(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left)\dot{\phi }\right]$
$\Rightarrow {\mathit{u}}^{\prime }\cdot {\mathit{u}}^{\prime }$	$=$	$[(y_c-y^{\prime })(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}})\dot{\phi }{]}^2+[x^{\prime }\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\dot{\phi }{]}^2$
	$=$	$\frac{{\dot{\phi }}^2}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}[(y_c-y^{\prime }{)}^2{x}_{\mathrm{m}\mathrm{a}\mathrm{x}}^4+(x^{\prime }{)}^2{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}^4]$
	$=$	$({u_0}^{\prime }{)}^2{\dot{\phi }}^2.$

Riemann Flow

STEP #5

Example Type I Ellipsoid (see also) $\frac{b}{a}=\frac{a_2}{a_1}$ 1.25 $\frac{c}{a}=\frac{a_3}{a_1}$ 0.4703 ${\mathrm{\Omega }}_2$ 0.3639 ${\mathrm{\Omega }}_3$ 0.6633 ${\tan }^{-1}\left[\frac{{\mathrm{\Omega }}_3}{{\mathrm{\Omega }}_2}\right]$ 61.25° ${\zeta }_2$ -2.2794 ${\zeta }_3$ -1.9637 ${\tan }^{-1}\left[\frac{{\zeta }_3}{{\zeta }_2}\right]$ 40.74° ${\beta }_{+}$ 1.13449 (1.13332) ${\gamma }_{+}$ 1.8052

As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids — see also our separate discussion — [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x₁, x₂, x₃) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating body coordinate frame, the three component expressions are,

$\dot{x}=u_1=\hat{\mathit{ı}}\cdot \mathit{u}$	$=$	$(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_{3}y-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_{2}z$	$=$	$-\left[\frac{a^2}{a^2+b^2}\right]{\zeta }_{3}y+\left[\frac{a^2}{a^2+c^2}\right]{\zeta }_{2}z,$
$\dot{y}=u_2=\hat{\mathit{ȷ}}\cdot \mathit{u}$	$=$	$-\gamma {\mathrm{\Omega }}_{3}x$	$=$	$+\left[\frac{b^2}{a^2+b^2}\right]{\zeta }_{3}x,$
$\dot{z}=u_3=\hat{\mathit{k}}\cdot \mathit{u}$	$=$	$+\beta {\mathrm{\Omega }}_{2}x$	$=$	$-\left[\frac{c^2}{a^2+c^2}\right]{\zeta }_{2}x,$

where,

$\beta$

$=$

$-\left[\frac{c^2}{a^2+c^2}\right]\frac{{\zeta }_2}{{\mathrm{\Omega }}_2}$

and,

$\gamma$

$=$

$-\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{{\mathrm{\Omega }}_3}.$

In order to transform Riemann's velocity vector from the body frame (unprimed) to the "tipped orbit" frame (primed coordinates), we use the following mappings of the three unit vectors:

$\hat{\mathit{ı}}$ $\to$ ${\hat{\mathit{ı}}}^{\prime },$ $\hat{\mathit{ȷ}}$ $\to$ ${\hat{\mathit{ȷ}}}^{\prime }\cos \theta -{\hat{\mathit{k}}}^{\prime }\sin \theta ,$ $\hat{\mathit{k}}$ $\to$ ${\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathit{k}}}^{\prime }\cos \theta .$

$x$ $\to$ $x^{\prime },$ $y$ $\to$ $y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$ $z-z_0$ $\to$ $y^{\prime }\sin \theta +z^{\prime }\cos \theta .$

In the tipped frame, we find,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )]+[{\hat{\mathit{k}}}^{\prime }\sin \theta -{\hat{\mathit{ȷ}}}^{\prime }\cos \theta ]\left[\gamma {\mathrm{\Omega }}_3{x}^{\prime }\right]+[{\hat{\mathit{ȷ}}}^{\prime }\sin \theta +{\hat{\mathit{k}}}^{\prime }\cos \theta ]\left[\beta {\mathrm{\Omega }}_2{x}^{\prime }\right]$
	$=$	${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta -z^{\prime }\sin \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(z_0+y^{\prime }\sin \theta +z^{\prime }\cos \theta )]+{\hat{\mathit{ȷ}}}^{\prime }[\beta {\mathrm{\Omega }}_2{x}^{\prime }\cdot \sin \theta -\gamma {\mathrm{\Omega }}_3{x}^{\prime }\cdot \cos \theta ]+{\hat{\mathit{k}}}^{\prime }[\beta {\mathrm{\Omega }}_2{x}^{\prime }\cdot \cos \theta +\gamma {\mathrm{\Omega }}_3{x}^{\prime }\cdot \sin \theta ].$

In order for the ${\mathit{k}}^{\prime }$ component to be zero in the tipped plane, we must choose the tipping angle such that,

$\tan \theta$

$=$

$-\frac{\beta {\mathrm{\Omega }}_2}{\gamma {\mathrm{\Omega }}_3}=-0.344793\Rightarrow \theta =-19.0238^{\circ }.$

And if we examine the flow only in the tipped x'-y' plane, then we should set $z^{\prime }=-z_0/\cos \theta$. These two constraints lead to the velocity expression,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

$=$

${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta +z_0\tan \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )]+{\hat{\mathit{ȷ}}}^{\prime }\underset{\dot{\phi }{y}_{\mathrm{m}\mathrm{a}\mathrm{x}}/x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\underbrace{[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]}}{x}^{\prime }.$

As we have indicated, this ${\hat{\mathit{ȷ}}}^{\prime }$ component will match our Step #4 velocity expression if,

$\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\dot{\phi }$	$=$	$\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta$
	$=$	$\left[\frac{1}{1+{\tan }^2\theta }{]}^{1/2}\right[\beta {\mathrm{\Omega }}_2\tan \theta -\gamma {\mathrm{\Omega }}_3]$
	$=$	$-\left[\frac{{\gamma }^2{\mathrm{\Omega }}_3^2}{{\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2}{]}^{1/2}\right[\frac{{\beta }^2{\mathrm{\Omega }}_2^2}{\gamma {\mathrm{\Omega }}_3}+\gamma {\mathrm{\Omega }}_3]$
	$=$	$-[{\beta }^2{\mathrm{\Omega }}_2^2+{\gamma }^2{\mathrm{\Omega }}_3^2{]}^{1/2}.$

Rewriting the ${\hat{\mathit{ı}}}^{\prime }$ component, we have,

$(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta +z_0\tan \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )$	$=$	$y^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3\cos \theta -(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2\sin \theta ]+(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(z_0\tan \theta )$
	$=$	$y^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2\tan \theta ][\frac{1}{1+{\tan }^2\theta }{]}^{1/2}-(\frac{a}{b}{)}^2\beta {\mathrm{\Omega }}_2{z}_0$
	$=$	$y^{\prime }\left[\right(\frac{a}{b}{)}^2{\gamma }^2{\mathrm{\Omega }}_3^2+\left(\frac{a}{c}{)}^2{\beta }^2{\mathrm{\Omega }}_2^2\right][\frac{1}{{\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2}{]}^{1/2}-(\frac{a}{b}{)}^2\beta {\mathrm{\Omega }}_2{z}_0.$

Hence,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

$=$

${\hat{\mathit{ı}}}^{\prime }\{y^{\prime }\underset{-\dot{\phi }{x}_{\mathrm{m}\mathrm{a}\mathrm{x}}/y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\underbrace{\left[\right(\frac{a}{b}{)}^2{\gamma }^2{\mathrm{\Omega }}_3^2+\left(\frac{a}{c}{)}^2{\beta }^2{\mathrm{\Omega }}_2^2\right][\frac{1}{{\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2}{]}^{1/2}}}-(\frac{a}{b}{)}^2\beta {\mathrm{\Omega }}_2{z}_0\}+{\hat{\mathit{ȷ}}}^{\prime }[\dot{\phi }\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)]x^{\prime }.$

That is to say, we need to set,

$\dot{\phi }\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)$

$=$

$-[c^2{\gamma }^2{\mathrm{\Omega }}_3^2+b^2{\beta }^2{\mathrm{\Omega }}_2^2]\left[\frac{1}{{\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2}{]}^{1/2}\right(\frac{a^2}{b^2{c}^2}).$

When this is combined with the constraint set by the ${\hat{\mathit{ȷ}}}^{\prime }$ component, we find,

${\dot{\phi }}^2=\dot{\phi }\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\cdot \dot{\phi }\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)$

$=$

$+[c^2{\gamma }^2{\mathrm{\Omega }}_3^2+b^2{\beta }^2{\mathrm{\Omega }}_2^2]\left(\frac{a^2}{b^2{c}^2}\right)=(1.29930{)}^2,$

and, hence,

$(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2$	$=$	$[c^2{\gamma }^2{\mathrm{\Omega }}_3^2+b^2{\beta }^2{\mathrm{\Omega }}_2^2]\left[\frac{1}{{\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2}{]}^{1/2}\right(\frac{a^2}{b^2{c}^2}\left)\right[{\beta }^2{\mathrm{\Omega }}_2^2+{\gamma }^2{\mathrm{\Omega }}_3^2{]}^{-1/2}$
	$=$	$\left[\frac{c^2{\gamma }^2{\mathrm{\Omega }}_3^2+b^2{\beta }^2{\mathrm{\Omega }}_2^2}{{\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2}\right]\left(\frac{a^2}{b^2{c}^2}\right)=(1.02585{)}^2.$

Finally, then,

$y_c\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\dot{\phi }$	$=$	$-(\frac{a}{b}{)}^2\beta {\mathrm{\Omega }}_2{z}_0$
$\Rightarrow \frac{y_c}{z_0}$	$=$	$-\left(\frac{a}{b}{)}^2\beta {\mathrm{\Omega }}_2\right\{\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\dot{\phi }{\}}^{-1}$
	$=$	$c^2\beta {\mathrm{\Omega }}_2[c^2{\gamma }^2{\mathrm{\Omega }}_3^2+b^2{\beta }^2{\mathrm{\Omega }}_2^2{]}^{-1}[{\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2{]}^{1/2}=0.19823.$

RESULT 2 (different from Result 1 and Result 3, above)

$\frac{y_0}{z_0}$ $=$ $-\frac{\sin \theta }{b^2{\kappa }^2}$

Reconcile Results Differences

Before calling upon any of Riemann's model parameters, from geometric considerations alone we should be able to determine exactly what the expression is for any off-center ellipse that results from slicing — at a tipped angle — the chosen ellipsoid.

Figure 1
$x$ $=$ $x^{\prime },$ $y$ $=$ $y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$ $(z-z_0)$ $=$ $z^{\prime }\cos \theta +y^{\prime }\sin \theta .$		$x^{\prime }$ $=$ $x,$ $y^{\prime }$ $=$ $y\cos \theta +(z-z_0)\sin \theta ,$ $z^{\prime }$ $=$ $(z-z_0)\cos \theta -y\sin \theta .$

Body Frame

As has been shown in our accompanying discussion, we obtain the following,

Intersection Expression
$1-\frac{x^2}{a^2}$	$=$	$y^2\left[\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2}\right]+y\left[\frac{2z_0\tan \theta }{c^2}\right]+\frac{z_0^2}{c^2},$

as long as z₀ lies within the range,

$z_0^2$

$\le$

$c^2+b^2{\tan }^2\theta .$

Given the values of $a,b,c,\theta ,z_0$, we can immediately map this to the tipped plane to obtain the surface-intersection function, $x^{\prime }(y^{\prime })$. Specifically we find, $x^{\prime }$ $=$ $a\{1-[(y^{\prime }\cos \theta -{\xcancel{z^{\prime }}}^0\sin \theta {)}^2(\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2})+(y^{\prime }\cos \theta -{\xcancel{z^{\prime }}}^0\sin \theta )(\frac{2z_0\tan \theta }{c^2})+\frac{z_0^2}{c^2}]{\}}^{1/2}$   $=$ $a\{1-[(y^{\prime }\cos \theta {)}^2(\frac{c^2+b^2{\tan }^2\theta }{b^2{c}^2})+y^{\prime }\cos \theta (\frac{2z_0\tan \theta }{c^2})+\frac{z_0^2}{c^2}]{\}}^{1/2}$

Along the tipped $y^{\prime }$ axis, two points will mark the ends of the x'-y' orbit; they are identified by the roots of this Intersection Expression when x = 0. That is, by the roots of,

$0$

$=$

$y^2\left[\frac{{\kappa }^2}{{\cos }^2\theta }\right]+y\left[\frac{2z_0\tan \theta }{c^2}\right]+[\frac{z_0^2}{c^2}-1],$

where,

${\kappa }^2$

$\equiv$

$\frac{c^2{\cos }^2\theta +b^2{\sin }^2\theta }{b^2{c}^2}.$

The roots are …

Scratch notes: $y_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}$ $=$ $\frac{B}{2A}\{\pm [1-\frac{4AC}{B^2}{]}^{1/2}-1\}$ where, $\frac{4AC}{B^2}=\frac{4{\kappa }^2}{{\cos }^2\theta }[\frac{z_0^2}{c^2}-1][\frac{2z_0\tan \theta }{c^2}{]}^{-2}=\frac{{\kappa }^2}{{\cos }^2\theta }[\frac{c^2(z_0^2-c^2)}{z_0^2{\tan }^2\theta }]=[\frac{c^2{\kappa }^2(z_0^2-c^2)}{z_0^2{\sin }^2\theta }]$

$y_{\mathrm{e}\mathrm{d}\mathrm{g}\mathrm{e}}$	$=$	$\left[\frac{z_0\sin \theta \cos \theta }{c^2{\kappa }^2}\right]\{\pm [1-\frac{c^2{\kappa }^2(z_0^2-c^2)}{z_0^2{\sin }^2\theta }{]}^{1/2}-1\}$
	$=$	$\left[\frac{\cos \theta }{c^2{\kappa }^2}\right]\{\pm [z_0^2{\sin }^2\theta +c^2{\kappa }^2(c^2-z_0^2){]}^{1/2}-z_0\sin \theta \}.$

Hereafter we will use $y_p$ to denote the "plus" root, and $y_m$ to denote the "minus" root; that is,

$y_p$	$\equiv$	$\left[\frac{\cos \theta }{c^2{\kappa }^2}\right]\left\{\right[z_0^2{\sin }^2\theta +c^2{\kappa }^2(c^2-z_0^2){]}^{1/2}-z_0\sin \theta \},$
$y_m$	$\equiv$	$-\left[\frac{\cos \theta }{c^2{\kappa }^2}\right]\left\{\right[z_0^2{\sin }^2\theta +c^2{\kappa }^2(c^2-z_0^2){]}^{1/2}+z_0\sin \theta \}.$

If tanθ is positive … Quadrant 1 ⇒ both sinθ and cosθ are positive. Quadrant 3 ⇒ both sinθ and cosθ are negative. If tanθ is negative … Quadrant 2 ⇒ sinθ is positive but cosθ is negative. Quadrant 4 ⇒ sinθ is negative while cosθ are positive. Taking numerical values from our chosen Example Model — and using z0 = ± 0.25 as our 1st test cases — we have: $\tan \theta$ $=$ $-\frac{\beta {\mathrm{\Omega }}_2}{\gamma {\mathrm{\Omega }}_3}=-0.344793\Rightarrow \theta =-19.0238^{\circ }.$ ${\kappa }^2$ $\equiv$ $\frac{c^2{\cos }^2\theta +b^2{\sin }^2\theta }{b^2{c}^2}=1.05238.$ $\mathrm{T}\mathrm{E}\mathrm{R}\mathrm{M}\mathrm{1}$ $\equiv$ $z_0^2{\sin }^2\theta +c^2{\kappa }^2(c^2-z_0^2)=0.043577$    (for z0 = ± 0.25). z0 = +0.25 and θ in QUADRANT #4 (sinθ is negative while cosθ is positive): $y_p$ $\equiv$ $\left[\frac{\cos \theta }{c^2{\kappa }^2}\right]\left\{\right[\mathrm{T}\mathrm{E}\mathrm{R}\mathrm{M}\mathrm{1}{]}^{1/2}-z_0\sin \theta \}=1.1788,$ $y_m$ $\equiv$ $-\left[\frac{\cos \theta }{c^2{\kappa }^2}\right]\left\{\right[\mathrm{T}\mathrm{E}\mathrm{R}\mathrm{M}\mathrm{1}{]}^{1/2}+z_0\sin \theta \}=-0.5169.$ $z_p$ $\equiv$ $-c[1-(\frac{y_p}{b}{)}^2{]}^{1/2}=-0.15645,$ $z_m$ $\equiv$ $c[1-(\frac{y_m}{b}{)}^2{]}^{1/2}=0.42821,$

$|z_0{|}_{\mathrm{m}\mathrm{a}\mathrm{x}}=0.63792$ $z_0$ $y_p$ $z_p$ $y_m$ $z_m$ $+0.6379$ $+0.8511$ $+0.3444$ $+0.8379$ $+0.3490$ $+0.60$ $+1.1073$ $+0.2182$ $+0.4814$ $+0.4340$ $+0.55$ $+1.1950$ $+0.1380$ $+0.2613$ $+0.4599$ $+0.50$ $+1.2342$ $+0.0744$ $+0.0897$ $+0.4691$ $+0.45$ $+1.2489$ $-0.0194$ $-0.0574$ $+0.4698$ $+0.40$ $+1.2474$ $-0.0301$ $-0.1883$ $+0.4649$ $+0.35$ $+1.2338$ $-0.0754$ $-0.3071$ $+0.4559$ $+0.30$ $+1.2105$ $-0.1174$ $-0.4161$ $+0.4435$ + 0.25 + 1.1788 - 0.1564 - 0.5169 + 0.4282 $+0.20$ $+1.1399$ $-0.1930$ $-0.6103$ $+0.4104$ $+0.15$ $+1.0943$ $-0.2273$ $-0.6971$ $+0.3904$ $+0.10$ $+1.0426$ $-0.2595$ $-0.7778$ $+0.3682$ $+0.05$ $+0.9849$ $-0.2896$ $-0.8525$ $+0.3439$ $+0.00$ $+0.9216$ $-0.3177$ $-0.9216$ $+0.3177$ $-0.05$ $+0.8525$ $-0.3439$ $-0.9849$ $+0.2895$ $-0.10$ $+0.7778$ $-0.3682$ $-1.0426$ $+0.2595$ etc. $-0.6379$ $-0.8379$ $-0.3490$ $-0.8511$ $-0.3444$

The y-coordinate of the center of the orbit will lie halfway between these two "edges". That is (numerical example given for the case of z₀ = + 0.25),

$y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}$

$=$

$\frac{1}{2}[y_p+y_m]=+0.3310.$

Correspondingly, the vertical (z) location of the orbit center in the body frame is given by the expression,

$z_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}$

$=$

$y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}\tan \theta +z_0=+0.1359.$

The line that runs parallel to the x-axis — lies perpendicular to the y-z plane — and that passes through this "center" location intersects the surface of the ellipsoid at a value of x that is obtained by plugging $y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}$ into the Intersection Expression. That is,

$\frac{x_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}}{a}$

$=$

$\{1-y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}^2[\frac{{\kappa }^2}{{\cos }^2\theta }]-y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}[\frac{2z_0\tan \theta }{c^2}]-\frac{z_0^2}{c^2}{\}}^{1/2}=0.92001;$

along the relevant orbit, this is also the maximum value of x.

Tipped Plane

We use the expressions in the right panel of Figure 1, above to transform (x, y, z) body coordinates to (x', y', z') tipped-frame coordiantes. Given that $x^{\prime }=x$, we appreciate that the x'-coordinate of the orbit center is zero, and the maximum value $(x{\text{'}}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}})$ that is encountered along the relevant orbit is the same as the value of $x_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}$ as determined in the body (unprimed) frame.

The z'-coordinate of the orbit center is,

$z{\text{'}}_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}$	$=$	$(z_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}-z_0)\cos \theta -y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}\sin \theta$
	$=$	$(y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}\tan \theta )\cos \theta -y_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}\sin \theta$
	$=$	$0.$

Finally, in the tipped plane, the maximum (subscript_p) and minimum (subscript_m) values of y' are,

$y{\text{'}}_p$	$=$	$(z_p-z_0)\sin \theta +y_p\cos \theta =1.2469,$
$y{\text{'}}_m$	$=$	$(z_m-z_0)\sin \theta +y_m\cos \theta =-0.5467,$
$\Rightarrow y{\text{'}}_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}$	$=$	$\frac{1}{2}[{y_p}^{\prime }+{y_m}^{\prime }]=0.3501.$
$\Rightarrow y{\text{'}}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}$	$=$	$y{\text{'}}_p-y{\text{'}}_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}=0.8968.$

So, in the tipped, x'-y' plane, the elliptical orbit that corresponds to z₀ = + 0.25 should be described by the expression,

$1$

$=$

$[\frac{x^{\prime }}{x_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}}{]}^2+[\frac{(y^{\prime }-y{\text{'}}_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}})}{y{\text{'}}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}}{]}^2.$

NOTE:

• $y{\text{'}}_{\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}}/z_0=0.350096/0.25=1.40038.$
• $x_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}/y{\text{'}}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}=0.92001/0.896819=1.0259.$

At a minimum these numerical values should be compared to the Riemann model parameters computed in our earlier (Pt. 2) examination.

Various Coordinate Frames

Tipped Orbit Planes

Summary

In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle $\theta$ about the x-axis of the body. As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = constant and dz'/dt = 0, and the planar orbit is defined by the expression for an,

Off-Center Ellipse
$1$	$=$	$[\frac{x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2+[\frac{y^{\prime }-y_c(z^{\prime })}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2.$

Tipped Orbit Frame (yellow, primed) Given that b/a = 1.25 and c/a = 0.4703 for our chosen Example Type I Ellipsoid, we find that, $\theta =-1.18122\mathrm{r}\mathrm{a}\mathrm{d}=-67.68^{\circ }$.

Notice that the offset, $y_c$, is a function of the tipped plane's vertical coordinate, $z^{\prime }$. As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,

$x^{\prime }$	$=$	$x_{\mathrm{m}\mathrm{a}\mathrm{x}}\cos (\dot{\phi }t)$	and,	$y^{\prime }-y_c$	$=$	$y_{\mathrm{m}\mathrm{a}\mathrm{x}}\sin (\dot{\phi }t),$
${\dot{x}}^{\prime }$	$=$	$-x_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }\cdot \sin (\dot{\phi }t)=(y_c-y^{\prime })\left[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }$	and,	${\dot{y}}^{\prime }$	$=$	$y_{\mathrm{m}\mathrm{a}\mathrm{x}}\dot{\phi }\cdot \cos (\dot{\phi }t)=x^{\prime }\left[\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right]\dot{\phi }.$

We have determined that (numerical value given for our chosen example Type I ellipsoid),

$\tan \theta$	$=$	$-\frac{b^2\beta {\mathrm{\Omega }}_2}{c^2\gamma {\mathrm{\Omega }}_3}=-2.43573,$
This definition of tan(θ) is inconsistent with all others!

where, as has also been specified in an accompanying discussion,

$\beta$

$=$

$-\left[\frac{c^2}{a^2+c^2}\right]\frac{{\zeta }_2}{{\mathrm{\Omega }}_2}=+1.13451$

and,

$\gamma$

$=$

$-\left[\frac{b^2}{a^2+b^2}\right]\frac{{\zeta }_3}{{\mathrm{\Omega }}_3}=+1.80518.$

We also have determined that,

$[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^4$	$=$	$\frac{a^4(c^4{\gamma }^2{\mathrm{\Omega }}_3^2+b^4{\beta }^2{\mathrm{\Omega }}_2^2)}{b^4{c}^4({\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2)}\Rightarrow \frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}=1.26218,$
${\dot{\phi }}^4$	$=$	$\frac{a^4}{b^4{c}^4}({\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2)(c^4{\gamma }^2{\mathrm{\Omega }}_3^2+b^4{\beta }^2{\mathrm{\Omega }}_2^2)\Rightarrow \dot{\phi }=1.59862,$
$\frac{y_c}{z_0}$	$=$	$-\sin \theta \Rightarrow \frac{y_c}{z_0}=-0.92507.$

Demonstration

In order to transform a vector from the "tipped orbit" frame (primed coordinates) to the "body" frame (unprimed), we use the following mappings of the three unit vectors:

${\hat{\mathit{ı}}}^{\prime }$ $\to$ $\hat{\mathit{ı}},$ ${\hat{\mathit{ȷ}}}^{\prime }$ $\to$ $\hat{\mathit{ȷ}}\cos \theta +\hat{\mathit{k}}\sin \theta ,$ ${\hat{\mathit{k}}}^{\prime }$ $\to$ $-\hat{\mathit{ȷ}}\sin \theta +\hat{\mathit{k}}\cos \theta .$

Given that, by design in our "tipped orbit" frame, there is no vertical motion — that is, ${\dot{z}}^{\prime }=0$ — mapping the (primed coordinate) velocity to the body (unprimed) coordinate is particularly straightforward. Specifically,

${\mathit{u}}^{\prime }$	$=$	${\hat{\mathit{ı}}}^{\prime }{\dot{x}}^{\prime }+{\hat{\mathit{ȷ}}}^{\prime }{\dot{y}}^{\prime }+{\hat{\mathit{k}}}^{\prime }{\xcancel{{\dot{z}}^{\prime }}}^0$
	$\to$	$\hat{\mathit{ı}}{\dot{x}}^{\prime }+[\hat{\mathit{ȷ}}\cos \theta +\hat{\mathit{k}}\sin \theta ]{\dot{y}}^{\prime }$
	$=$	$\hat{\mathit{ı}}\{(y_c-y^{\prime })(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left)\dot{\phi }\right\}+[\hat{\mathit{ȷ}}\cos \theta +\hat{\mathit{k}}\sin \theta ]\left\{x^{\prime }\right(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\left)\dot{\phi }\right\}.$

Recognizing, as before, that the relevant coordinate mapping is,

$x$ $=$ $x^{\prime },$ $y$ $=$ $y^{\prime }\cos \theta -z^{\prime }\sin \theta ,$ $(z-z_0)$ $=$ $z^{\prime }\cos \theta +y^{\prime }\sin \theta .$

$x^{\prime }$ $=$ $x,$ $y^{\prime }$ $=$ $y\cos \theta +(z-z_0)\sin \theta ,$ $z^{\prime }$ $=$ $(z-z_0)\cos \theta -y\sin \theta .$

we have,

${\mathit{u}}^{\prime }$

$\to$

$\hat{\mathit{ı}}\dot{\phi }\left(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\{y_c-y\cos \theta -(z-z_0)\sin \theta \}+\hat{\mathit{ȷ}}\dot{\phi }\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\{x\cos \theta \}+\hat{\mathit{k}}\dot{\phi }\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)\{x\sin \theta \}.$

Therefore, as viewed from the body frame, the individual velocity components are,

$\hat{\mathit{ȷ}}\cdot {\mathit{u}}^{\prime }$	$=$	$\dot{\phi }\left(\frac{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)x\cos \theta$
	$=$	$x\cdot \left\{\frac{b^4{c}^4({\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2)}{a^4(c^4{\gamma }^2{\mathrm{\Omega }}_3^2+b^4{\beta }^2{\mathrm{\Omega }}_2^2)}\frac{a^4}{b^4{c}^4}\right({\gamma }^2{\mathrm{\Omega }}_3^2+{\beta }^2{\mathrm{\Omega }}_2^2)(c^4{\gamma }^2{\mathrm{\Omega }}_3^2+b^4{\beta }^2{\mathrm{\Omega }}_2^2){\}}^{1/4}\frac{c^2\gamma {\mathrm{\Omega }}_3}{[c^4{\gamma }^2{\mathrm{\Omega }}_3^2+b^4{\beta }^2{\mathrm{\Omega }}_2^2{]}^{1/2}}$

Test Orthogonality

Let's see if the Riemann fluid velocity vector is everywhere tangent to our identified off-center elliptical (Lagrangian-particle) orbital trajectories. We can determine this by first deriving an expression for the vector normal to the trajectories, then see if the dot product of this vector and the velocity vector is everywhere zero.

The unit vector that is normal to a trajectory is obtained from the (appropriately normalized) gradient of the function,

$f(x^{\prime },y^{\prime })$

$\equiv$

$[\frac{x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2+[\frac{y^{\prime }-y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{]}^2-1.$

We find, first,

$\mathrm{\nabla }f$

$=$

${\hat{\mathit{ı}}}^{\prime }\left[\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]+{\hat{\mathit{ȷ}}}^{\prime }\left[\frac{2(y^{\prime }-y_c)}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]-{\hat{\mathit{k}}}^{\prime }\left[\frac{2(y^{\prime }-y_c)}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]\frac{\partial y_c}{\partial z^{\prime }},$

where, drawing from Step #2, above,

$\frac{y_c}{z_0}$ $=$ $-\frac{\sin \theta }{c^2{\kappa }^2},$ $z_0^2$ $\le$ $c^2+b^2{\tan }^2\theta ,$ $y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ $=$ $\frac{1}{{\kappa }^2}[1-\frac{z_0^2}{c^2}-\frac{z_0\sin \theta }{c^2}],$ $x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ $=$ $a^2[1-\frac{z_0^2}{c^2}-\frac{z_0\sin \theta }{c^2}].$ Note as well that, $(\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}}{)}^2$ $=$ $a^2{\kappa }^2=\frac{a^2}{b^2{c}^2}[c^2{\cos }^2\theta +b^2{\sin }^2\theta ].$

Next, after setting $\tan \theta =-(\beta {\mathrm{\Omega }}_2/\gamma {\mathrm{\Omega }}_3)$, and pulling from Step #3, above, we have,

${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$

$=$

${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta +z_0\tan \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )]+{\hat{\mathit{ȷ}}}^{\prime }[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]x^{\prime }.$

Stick With Rotating Frame

The dot product of these two vectors is,

$\mathrm{\nabla }f\cdot {{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$	$=$	$\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta +z_0\tan \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )]\left[\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]+[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]x^{\prime }\left[\frac{2(y^{\prime }-y_c)}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]$
	$=$	$\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )]\left[\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]+\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(z_0\tan \theta )\left]\right[\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}]$
		$+[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]x^{\prime }\left[\frac{2y^{\prime }}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]-[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]x^{\prime }\left[\frac{2y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]$
	$=$	$2x^{\prime }{y}^{\prime }\left\{\right[(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(\cos \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(\sin \theta )\left]\right[\frac{1}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}]+[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta \left]\right[\frac{1}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left]\right\}$
		$+2x^{\prime }\left\{\right[(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3\tan \theta ]\left[\frac{z_0}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]-[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]\left[\frac{y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]\}.$

Now, drawing from the various above "boxed" relations and examining the two terms separately, we first find,

TERM1	$=$	$\frac{2x^{\prime }{y}^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left(\frac{a^2}{b^2{c}^2}\right)\left\{\right[c^2\gamma {\mathrm{\Omega }}_3(\cos \theta )-b^2\beta {\mathrm{\Omega }}_2(\sin \theta )]+[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta \left]\right[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left]\right(\frac{b^2{c}^2}{a^2}\left)\right\}$
	$=$	$\frac{2x^{\prime }{y}^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left(\frac{a^2}{b^2{c}^2}\right)\left\{\right[c^2(\cos \theta )+b^2\tan \theta (\sin \theta )]-[\tan \theta \sin \theta +\cos \theta \left]\right[c^2{\cos }^{}\theta +b^2{\sin }^{}\theta \left]\right\}\gamma {\mathrm{\Omega }}_3$
	$=$	$\frac{2x^{\prime }{y}^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left(\frac{a^2}{b^2{c}^2}\right)\left\{\right[c^2+b^2{\tan }^2\theta ]-[{\tan }^2\theta +1\left]\right[c^2{\cos }^2\theta +b^2{\sin }^2\theta \left]\right\}\gamma {\mathrm{\Omega }}_3\cos \theta$
	$=$	$\frac{2x^{\prime }{y}^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left(\frac{a^2}{b^2{c}^2}\right)\{c^2+b^2{\tan }^2\theta -[{\tan }^2\theta +1\left]\right[c^2{\cos }^2\theta ]-[{\tan }^2\theta +1\left]\right[b^2{\sin }^2\theta \left]\right\}\gamma {\mathrm{\Omega }}_3\cos \theta$
	$=$	$\frac{2x^{\prime }{y}^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left(\frac{a^2}{b^2{c}^2}\right)\{c^2+b^2{\tan }^2\theta -c^2-b^2{\tan }^2\theta \}\gamma {\mathrm{\Omega }}_3\cos \theta$
	$=$	$0.$

And, in order for the second term to go to zero as well, we need …

$0$	$=$	$\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left\{\right[(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3\tan \theta ]z_0-y_c[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta ]\left[\frac{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]\}$
	$=$	$\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left\{\right[c^2\tan \theta ]z_0+y_c[(\tan \theta )\sin \theta +\cos \theta ](c^2{\cos }^{}\theta +b^2{\sin }^{}\theta )\}\left(\frac{a^2}{b^2{c}^2}\right)\gamma {\mathrm{\Omega }}_3$
	$=$	$\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left\{\right[c^2\tan \theta ]z_0+y_c\cos \theta (c^2+b^2{\tan }^{}\theta )\}\left(\frac{a^2}{b^2{c}^2}\right)\gamma {\mathrm{\Omega }}_3$
$\Rightarrow y_c\cos \theta (c^2+b^2{\tan }^{}\theta )$	$=$	$-[c^2\tan \theta ]z_0$
$\Rightarrow \frac{y_c}{z_0}$	$=$	$-\frac{c^2\tan \theta }{\cos \theta (c^2+b^2{\tan }^{}\theta )}=-\frac{c^2{\tan }^2\theta }{\sin \theta (c^2+b^2{\tan }^{}\theta )}=-\frac{c^2\sin \theta }{(c^2{\cos }^2\theta +b^2{\sin }^2\theta )}=-\frac{\sin \theta }{b^2{\kappa }^2}.$

Try Shifting to (Quasi-) Inertial Frame

Let's adjust both remaining components of ${{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}$ to see what their equivalent rotating-frame expressions are. The relevant shift is,

${{\mathit{v}}^{\prime }}_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{f}\mathrm{t}}\equiv {\mathrm{\Omega }}^{\prime }\times {\mathit{x}}^{\prime }$

$=$

$\hat{\mathit{k}}{\mathrm{\Omega }}^{\prime }\times [{\hat{\mathit{ı}}}^{\prime }{x}^{\prime }+{\hat{\mathit{ȷ}}}^{\prime }{y}^{\prime }]=-{\hat{\mathit{ı}}}^{\prime }{\mathrm{\Omega }}^{\prime }{y}^{\prime }+{\hat{\mathit{ȷ}}}^{\prime }{\mathrm{\Omega }}^{\prime }{x}^{\prime },$

where,

${\mathrm{\Omega }}^{\prime }$

$=$

$[{\mathrm{\Omega }}_2^2+{\mathrm{\Omega }}_3^2{]}^{1/2}.$

We have, then,

${{\mathit{u}}^{\prime }}_{\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}\equiv {{\mathit{u}}^{\prime }}_{\mathrm{E}\mathrm{F}\mathrm{E}}+{{\mathit{v}}^{\prime }}_{\mathrm{s}\mathrm{h}\mathrm{i}\mathrm{f}\mathrm{t}}$

$=$

${\hat{\mathit{ı}}}^{\prime }\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta +z_0\tan \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )-{\mathrm{\Omega }}^{\prime }{y}^{\prime }]+{\hat{\mathit{ȷ}}}^{\prime }[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta +{\mathrm{\Omega }}^{\prime }]x^{\prime }$

The dot product of this expression with $\mathrm{\nabla }f$ is,

$\mathrm{\nabla }f\cdot {{\mathit{u}}^{\prime }}_{\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}}$	$=$	$\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(y^{\prime }\cos \theta +z_0\tan \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(y^{\prime }\sin \theta )-{\mathrm{\Omega }}^{\prime }{y}^{\prime }]\left[\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]+[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta +{\mathrm{\Omega }}^{\prime }]x^{\prime }\left[\frac{2(y^{\prime }-y_c)}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]$
	$=$	$\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(\cos \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(\sin \theta )-{\mathrm{\Omega }}^{\prime }]\left[\frac{2x^{\prime }{y}^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]+\left[\right(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(z_0\tan \theta )\left]\right[\frac{2x^{\prime }}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}]$
		$+[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta +{\mathrm{\Omega }}^{\prime }]x^{\prime }\left[\frac{2y^{\prime }}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]-[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta +{\mathrm{\Omega }}^{\prime }]x^{\prime }\left[\frac{2y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]$
	$=$	$2x^{\prime }{y}^{\prime }\left\{\right[(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3(\cos \theta )-(\frac{a}{c}{)}^2\beta {\mathrm{\Omega }}_2(\sin \theta )-{\mathrm{\Omega }}^{\prime }\left]\right[\frac{1}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}]+[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta +{\mathrm{\Omega }}^{\prime }\left]\right[\frac{1}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\left]\right\}$
		$+2x^{\prime }\left\{\right[(\frac{a}{b}{)}^2\gamma {\mathrm{\Omega }}_3\tan \theta ]\left[\frac{z_0}{x_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]-[\beta {\mathrm{\Omega }}_2\sin \theta -\gamma {\mathrm{\Omega }}_3\cos \theta +{\mathrm{\Omega }}^{\prime }]\left[\frac{y_c}{y_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}\right]\}.$

Now, drawing from the various above "boxed" relations and examining the two terms separately, we first find,

See Also

• Description of Riemann Type I Ellipsoids
• Riemann Type 1 Ellipsoids (old introduction)
• Construction Challenges (Pt. 1)
• Construction Challenges (Pt. 2)
• Construction Challenges (Pt. 3)
• Construction Challenges (Pt. 4)
• Construction Challenges (Pt. 5)
• Construction Challenges (Pt. 6)

• Related discussions of models viewed from a rotating reference frame:
  • PGE
  • NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.