ThreeDimensionalConfigurations/RiemannStype
Riemann S-Type Ellipsoids
| Riemann S-Type Ellipsoids |
|---|
As has been detailed in an accompanying chapter, the gravitational potential anywhere inside or on the surface, , of an homogeneous ellipsoid may be given analytically in terms of the following three coefficient expressions:
|
|
|
|
|
|
|
|
|
|
|
|
where, and are incomplete elliptic integrals of the first and second kind, respectively, with arguments,
|
|
and |
|
| [ EFE, Chapter 3, §17, Eq. (32) ] | ||
| TEST (part 1) Notation: Use in place of . |
||||||||||
| Numerical Recipes | ||||||||||
| (deg) | (rad) | (deg) | (rad) | |||||||
| 0.9 | 0.641 | 50.13357253 | 0.874995907 | 32.53852919 | 0.567904468 | 0.909025949 | 0.843118048 | 0.521450273 | 0.595131012 | 0.883418715 |
| (January, 2022) Howard Cohl's Mathematica evaluation with 20-digit precision | 0.52145 02732 81618 28861 | 0.59513 10119 32875 42194 | 0.88341 87147 85506 28946 | |||||||
Equilibrium Conditions for Riemann S-type Ellipsoids
We begin this section by quoting from the first paragraph in §II, p. 892 of 📚 S. Chandrasekhar (1965, ApJ, Vol. 142, pp. 890 - 961) — referred to in [EFE] as Publication XXV. "The problem that is to be considered … is that of a homogeneous mass, rotating uniformly with an angular velocity , with internal motions having a uniform vorticity in the direction of and in the frame of reference rotating with the angular velocity ." As did Chandrasekhar, we will find it useful to refer to the ratio of these highlighted frequencies as the key model parameter,
|
|
|
|
📚 Chandrasekhar (1965; XXV), p. 892, §II, Eq. (15)
[ EFE, §48, Eq. (31) ]
When relating our discussion to previous works, it also will be useful to recognize that the dimensionless frequency, , is related to the magnitude of the vorticity via the relation,
|
|
|
|
📚 Lebovitz & Lifschitz (1996), p. 700, §2, immediately following Eq. (1)
📚 Ou (2006), p. 551, §2, Eq. (17)
Based on Virial Equilibrium
Pulling from Chapter 7 — specifically, §48 — of [EFE], we understand that the semi-axis ratios, associated with Riemann S-type ellipsoids are given by the roots of the equation,
|
|
|
|
| [ EFE, §48, Eq. (34) ] | ||
and the associated value of the square of the equilibrium configuration's angular velocity is,
|
|
|
|
| [ EFE, §48, Eq. (33) ] | ||
where,
|
|
|
|
| [ EFE, §21, Eq. (107) ] | ||
|
|
|
|
| [ EFE, §21, Eq. (105) ] See also the note immediately following §21, Eq. (127) | ||
|
In a subsection of a separate chapter, we show in detail how the above set of equilibrium conditions arises from the,
| ||||||
(Notice that if we set , this pair of expressions simplifies to the pair we have provided in a separate discussion of the equilibrium conditions for Jacobi ellipsoids.) Following Chandrasekhar's lead and eliminating between these two expressions, we obtain,
|
|
|
|
| [ EFE, §48, Eq. (35) ] | ||
For a given , this last expression determines the ratios of the axes of the ellipsoids that are compatible with equilibrium; and the value of , that is to be associated with a particular solution of this last expression, then follows from either one of the first two expressions. For convenience of evaluation and for greater clarity, let's rewrite this last (quadratic) equation in the form,
|
|
|
|
| TEST (part 2) | ||||||
| 0.9 | 0.641 | 0.387793362 | 0.207337649 | 0.247245200 | 3.797483556 | 3.818580687 |
| 0.38779 33613 22405 96490 | 0.20733 7650610469 45704 | (January, 2022) Howard Cohl's Mathematica evaluation with 20-digit precision | ||||
The pair of solutions is,
|
|
|
|
and the corresponding values of the angular velocity (in units of [G ρ]½) are provided by the expression,
|
|
|
|
As an aid in determining both values of the parameter, , we note as well that,
|
|
|
|
| TEST (part 2.1) | |||||||||||||||||||||||||||||||||||||||||||||||
| EFE Derivation | |||||||||||||||||||||||||||||||||||||||||||||||
| -0.268009 | 0.638310 | -0.1710727 | -0.133264 | 0.0850638 | -15.09117 | 0.0850638 | -1.28371 | -7.50390 | 0.638310 | ||||||||||||||||||||||||||||||||||||||
| Adjoint | |||||||||||||||||||||||||||||||||||||||||||||||
| -15.09117 | 0.085064 | -1.28371 | -7.50390 | 0.638310 | |||||||||||||||||||||||||||||||||||||||||||
|
Given the choice of FILL OUT THIS TABLE AS FOLLOWS:
|
|||||||||||||||||||||||||||||||||||||||||||||||
NOTE: The model that has been identified as the "negative" solution, , of the governing quadratic relation is precisely synonymous with the model that has been identified as the "adjoint" of the "positive" solution, . It should come as no surprise that the model labeled as is the model labeled as .
|
Essentially this same derivation can be found in §2 of 📚 Lebovitz & Lifschitz (1996), hereafter LL96 — see also our chapter discussion of this work. But instead of seeking solutions that are expressed in terms of the model-parameter pair , and the ratio, , it should be recognized that LL96 use, 
So, the frequency ratio that LL96 define immediately preceding their Eq. (5),
[For the example, , parameter values: ].
When rewritten in terms of , the above-derived quadratic equation for , namely,
becomes,
where,
[For the example, , we find, .]
| |||||||||||||||||||||||||||||||||
Based on Detailed Force Balance
The Steady-State Condition
As has been pointed out in our introductory discussion of the Principal Governing Equations, quite generally we can write the
Eulerian Representation
of the Euler Equation
as viewed from a Rotating Reference Frame
where, specifies the time-invariant rotation frequency of the frame and the orientation of the vector about which the frame spins. The condition for detailed force balance in a steady-state configuration is obtained by setting . If we furthermore make the substitution, , where is enthalpy — an equation of state relation that is appropriate for a barytropic system — we obtain,
Adopted Velocity Flow-Field
As 📚 Ou (2006) has pointed out [text that is taken directly from that publication appears here in an orange-colored font], the velocity field of a Riemann S-type ellipsoid as viewed from a frame rotating with angular velocity takes the following form:
|
|
|
|
📚 Lebovitz & Lifschitz (1996), p. 700, §2, Eq. (1)
📚 Ou (2006), p. 550, §2, Eq. (3)
where is a constant that determines the magnitude of the internal motion of the fluid, and the origin of the x-y coordinate system is at the center of the ellipsoid. This velocity field is designed so that velocity vectors everywhere are always aligned with elliptical stream lines by demanding that they be tangent to the equi-effective-potential contours, which are concentric ellipses.
|
Plugging Ou's expression for into the expression on the left-hand side of the steady-state Euler equation, we see that for Riemann S-type ellipsoids,
Alternatively, from a separate discussion of vector identities we realize that,
where, is the fluid vorticity. Plugging in Ou's expression for , we find that …
Hence, we again appreciate that, for Riemann S-type ellipsoids,
| ||||||||||||||||||||||||||
The steady-state Euler-equation specification therefore becomes,
Hence, within the configuration the following Bernoulli's function must be uniform in space:
where is a constant. It is customary to define an effective potential which is the sum of the gravitational potential and the system's centrifugal potential (as viewed from the rotating frame), namely,
in which case the statement of detailed force balance in Riemann S-type ellipsoids can be rewritten in the following deceptively simpler form:
Evaluation of the Gravitational Potential
Drawing from a separate discussion of the gravitational potential of homogeneous ellipsoids, we see that for Riemann S-type ellipsoids,
where, the normalization constant,
|
|
|
Implied Parameter Values
So, at the surface of the ellipsoid (where the enthalpy H = 0) on each of its three principal axes, the equilibrium conditions demanded by the expression for detailed force balance become, respectively:
- On the x-axis, where (x, y, z) = (a, 0, 0):
- On the y-axis, where (x, y, z) = (0, b, 0):
- On the z-axis, where (x, y, z) = (0, 0, c):
Using the result from "III" to replace the left-hand side of both relation "I" and relation "II", we find that,
|
|
|
|
and,
|
|
|
|
Multiplying the first of these two expressions by then subtracting it from the second gives,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Alternatively, just subtracting the first expression from the second gives,
|
|
|
|
|
|
|
|
|
|
|
|
We can eliminate between these last two expressions as follows: From the first of the two, we have
|
|
|
|
Hence, the second gives,
|
|
|
|
|
|
|
|
|
|
|
|
This is a quadratic equation whose solution gives and, in turn, . Specifically for Direct configurations, we find that,
where,
|
|
|
and, |
|
|
|
|
| TEST (part 3) | ||||||||||
| 0.9 | 0.641 | 0.521450273 | 0.595131012 | 0.883418715 | 0.414682903 | 0.054301271 | 0.407446048 | 0.007236855 | 1.131383892 | 0.150782130 |
The numerical values listed in the last two columns of this "part 3" test match the values listed above in "part 2" of our test for, respectively, and .
Relate EFE to Ou (2006)
As we have already acknowledged, according to Ou (2006), at any coordinate position inside or on the surface of the ellipsoid, , the three components of the velocity as viewed from a frame of rotation that is spinning at the equilibrium configuration's frequency, , are,
|
|
|
|
where, is an overall scale factor. But, according to §48 of EFE, we see that,
|
|
|
|
📚 Chandrasekhar (1965; XXV), p. 892, §II, Eq. (9)
where,
|
|
|
|
and, |
|
|
|
📚 Chandrasekhar (1965; XXV), p. 892, §II, Eq. (10)
and is the scalar magnitude of the vorticity vector, . The transformation from EFE's notation to the one used by Ou is, then,
|
|
|
|
and, |
|
|
|
|
|
|
|
which, gratifyingly agrees with Eq. (17) in 📚 Ou (2006). It is worth noting as well that, when viewed from the inertial reference frame, the velocity field is,
|
|
|
|
📚 Chandrasekhar (1965; XXV), p. 892, §II, Eq. (13)
Broken down into its Cartesian components, this is
|
|
|
|
|
|
|
|
|
|
|
|
📚 Chandrasekhar (1965; XXV), p. 892, §II, Eq. (14)
Summary
It is often useful to discuss the properties of Riemann S-type ellipsoids in the context of what we will refer to as the traditional "EFE Diagram" — a two-dimensional parameter space defined by the axis ratio ranges, 0 ≤ b/a ≤ 1 and 0 ≤ c/a ≤ 1. It is useful to appreciate at the outset, for example, that Riemann S-type ellipsoids only populate a subset of the EFE Diagram's entire parameter space. More specifically, they all lie between or on the two (self-adjoint) curves marked "X = -1" and "X = +1" in the EFE Diagram that is shown here, on the right. Keeping this in mind, we summarize here a sequence of steps that should be taken in order to construct and thereby quantitatively detail all of the physical properties that are associated with any Riemann S-type ellipsoid that lies in this allowed region of the EFE Diagram.
| Figure 1 |
 |
| Caption: See Figure 2, below |
- Specify numerical values for any two of the three key parameters: . The value of the third (unspecified) parameter can then be found by determining the root(s) of the virial-equilibrium-based expression,
[ EFE, §48, Eq. (35) ] - If you specified the values of and , then values of the three parameters, — as well as the related parameters, — can be immediately determined from the above general coefficient expressions and related relations as long as you have an algorithm that can be used to evaluate incomplete elliptic integrals of the first and second kind. The governing virial-equilibrium-based expression then becomes a quadratic equation whose pair of roots give two physically viable values of the parameter, ; we will refer to them as and
NOTE: If the chosen pair of axis ratios places your configuration above the Jacobi/Dedekind sequence in the familiar "EFE Diagram," then the parameter, , will invariably be negative; if it is below the Jacobi/Dedekind sequence, will invariably be positive.
NOTE as well: This is the method that we have used, below, in order to replicate various equilibrium configurations that have been studied by Ou (2006). - If, instead, you specified the value of and (only) one of the ellipsoid's axis ratios, then an iterative numerical scheme — such as a Newton Raphson method — will need to be used in order to determine a physically viable (real) root of this nonlinear, virial-equilibrium-based expression. This root will provide the value of the equilibrium ellipsoid's other axis ratio.
NOTE: The Jacobi/Dedelind sequence is determined in this manner by setting , then determining what value of the c/a axis ratio is consistent with various selected values of 0 < b/a ≤ 1. - If, as in step 1.B, only one value of the parameter, , is known, the other relevant value may be obtained from the relation,
In either case, if the model will be referred to as being a Jacobi-like — or, Direct — configuration because the magnitude of the configuration's spin frequency, , is larger than the magnitude of the frequency, , that characterizes internal motions (vorticity). On the other hand, if the model will be referred to as being a Dedekind-like — or, Adjoint — configuration because the internal motions dominate.
NOTE: A so-called self-adjoint model sequence will arise when for all values of the axis ratio, 0 < b/a ≤ 1. There are two such sequences, namely, when — this is the curve labeled, "X =+1" in the EFE Diagram shown here on the right — or when — this is the curve labeled, "X = - 1. In the familiar EFE diagram, these curves intersect the Maclaurin sequence (where, b/a = 1) when, respectively, and .
- If you specified the values of and , then values of the three parameters, — as well as the related parameters, — can be immediately determined from the above general coefficient expressions and related relations as long as you have an algorithm that can be used to evaluate incomplete elliptic integrals of the first and second kind. The governing virial-equilibrium-based expression then becomes a quadratic equation whose pair of roots give two physically viable values of the parameter, ; we will refer to them as and
-
Once a consistently specified set of parameters, and , is known, the configuration's spin frequency may be straightforwardly obtained from another virial-equilibrium-based expression, namely,
[ EFE, §48, Eq. (33) ] -
Once a consistently specified pair of parameters, and , is known, the configuration's vorticity can immediately be determined via the expression,
where,
-
At every location inside a Riemann S-type ellipsoid, the fluid vorticity must be related to the underlying velocity field via the expression, . In order for the vorticity to be uniform throughout the configuration — everywhere being represented by the vector, — we realize that the velocity field is properly described by the expression,
where, 📚 Lebovitz & Lifschitz (1996), p. 700, §2, Eq. (1)
📚 Lebovitz & Lifschitz (1996b), p. 930, §3, Eqs. (3.1) & (3.2)
📚 Ou (2006), p. 550, §2, Eqs. (3) & (17)
Maclaurin Spheroid Limit
Basic Relations
Expressions Supplied by EFE
In Chapter 7, §48(b) (pp. 137 - 138) of [EFE] , Chandrasekhar shows that "… a stable Maclaurin spheroid can be considered as a limiting form of a [S-type] Riemann ellipsoid." First, we recall that, as viewed from the inertial frame, each Maclaurin spheroid of eccentricity, , rotates uniformly with angular velocity,
|
|
||
|
[EFE], §32, pp. 77-78, Eqs. (4) & (6) |
||
Given the specified value of the semi-axis ratio, , the properties of the limiting S-type Riemann ellipsoid are given by the expressions,
|
|
|
|
| [EFE], Chapter 7, §48(b), p. 137, Eq. (60) | ||
and,
|
|
|
|
|
|
|
|
| [EFE], Chapter 7, §48(b), p. 137, Eqs. (58) & (61) | ||
where,
|
|
|
|
| [EFE], Chapter 3, §21, Eq. (105) | ||
Evaluating A11
As has been stated in a separate derivation, quite generally,
|
|
|
|
Now, in the case of Maclaurin spheroids, , so this integral expression becomes,
|
|
|
|
where, Before applying the limits, carrying out the integration gives,
|
|
|
|
|
[CRC] chapter on INTEGRALS, p. 408, Eq. (154) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
[CRC] chapter on INTEGRALS, p. 407, Eq. (148) |
||
|
|
|
|
Applying the limits then gives,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Derivation Check
At the top of p. 141 (§48) of [EFE] — see also Table VI on p. 142 — Chandrasekhar emphasizes that the point at which the self-adjoint (S-type) Riemann ellipsoid intersects the Maclaurin spheroid has . As Table I (p. 78) records, the Maclaurin spheroid having this eccentricity has At this point, therefore,
|
|
|
|
| [EFE], Chapter 7, §48(c), Eq. (141) | ||
Note as well that, from the above expression for (ζ3)2, we have,
|
|
|
|
|
|
|
|
as it should be.
For this same value of the eccentricity, we recognize as well that, . Therefore, drawing from the above expression for B11, we also deduce that,
|
|
|
|
| [EFE], Chapter 3, §21, Eq. (105) | ||
Hooray!! This matches the numerical value of determined above for . So it seems reasonable to conclude that the general expression, itself, is correct.
Frequency Ratio
Determination and Plot
Given that, for all Maclaurin spheroids,
|
|
|
|
|
|
|
|
|
[EFE], §17, p. 43, Eq. (36) |
||
we conclude that along the entire Maclaurin spheroid sequence, the index symbol,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
We can therefore write,
|
|
|
|
and, |
|
|
|
where,
|
|
|
|
REMINDER: For a given choice of the eccentricity, there are two viable solutions … the direct configuration and its adjoint. In the context of Riemann S-type ellipsoids (i.e., here), this pair of solutions arises from the choice of the sign in the expression for ; in the context of Type I Riemann ellipsoids, the pair arises from the choice of the sign in the STEP #3 determination of and . In both physical contexts, the direct (Jacobi-like) solution results from selecting the inferior sign while the adjoint (Dedekind-like) solution results from selecting the superior sign.
|
Figure 1: Parameter Variations Along the Maclaurin Spheroid Sequence |
|
 |
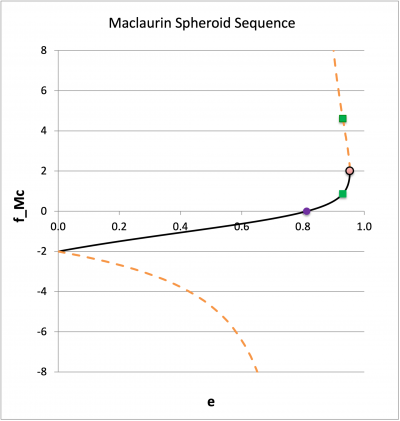 |
| Analogous to Figure 5 from §32, p. 79 of [EFE]; shows how the square of the normalized rotation frequency varies with eccentricity, along the (black-dotted) Maclaurin sequence and along the Jacobi sequence (series of purple circular markers). |
Each Riemann S-type ellipsoid sequence — uniquely identified by its frequency ratio, — intersects the Maclaurin spheroid sequence at a specific value of the meridional-plane eccentricity, Analogous to Figure 12 from §48, p. 139 of [EFE], this plot displays how varies with along the Maclaurin spheroid sequence; for a given , the solid black curve is associated with the direct configuration while the dashed orange curve is associated with the adjoint configuration. The circular, solid-purple marker identifies the point where the Jacobi sequence bifurcates from the Maclaurin spheroid sequence; bifurcation to the Dedekind sequence is not displayed here because its frequency ratio is off scale. The square, solid-green markers identify the location of the pair of models (direct/adjoint) for which is maximum (see the square, solid-green marker in the left-hand panel). The circular, solid-orange marker identifies the (degenerate) pair of models where the "" sequence bifurcates from the Maclaurin spheroid sequence. |
|
Drawing from one of our mathematics appendices, we know that when ,
|
| Table: Key Values Along the Limiting Maclaurin Spheroid Sequence | ||||||||||||
| Model | e | Direct | Adjoint | |||||||||
| Nonrotating Sphere & "" Bifurcation |
0.00000 | 0.00000 | Note: (a) |
Note: (a) |
Note: (a) |
Note: (a) |
||||||
| Jacobi/Dedekind Bifurcation | 0.81267 Note: (b) |
0.37423 Note: (b) |
Note: (c) |
Note: (c) |
Note: (c) |
Note: (c) |
Note: (c) |
Note: (c) |
Note: (c) |
|||
| "" Bifurcation | 0.952886702 | 0.440219895 | Note: (d) |
Note: (d) |
Note: (d) |
Note: (d) |
Note: (d) |
|||||
|
Notes: |
||||||||||||
Models Examined by Ou (2006)
In §2 of 📚 Ou (2006), immediately after equation (6), we find the following declaration: In direct configurations, ω > λ so the fluid motion is dominated by figure rotation; conversely, in an adjoint configuration, ω < λ so the fluid motion is dominated by internal motions.
His Tabulated Model Parameters
Table 1 (see below) lists a subset of the Riemann S-type ellipsoids that were studied by 📚 Ou (2006); properties of various so-called Direct configurations can be found in Ou's Table 1, while properties of various Adjoint configurations can be found in his Table 5. Each row of our Table 1 was constructed as follows:
- The pair of axis ratios associated with one of Ou's (2006) uniform-density, incompressible ellipsoid models (columns 1 and 2 from Ou's Table 1) has been copied into columns 1 and 2 of our table.
- Properties of Direct Configurations …
- The pair of parameter values that is required in order for this to be an equilibrium configuration — as specified by the above set of analytical expressions from EFE — is copied from, respectively, columns 11 and 13 of Ou's Table 1 into columns 3 and 4 of our table; in our table, the "analytic" subscript has been dropped from the column headings.
- The value of the equilibrium configuration's vorticity, — see column 5 of our table — has been determined from the expression,
- Column 6 of our table lists the value of the frequency ratio, .
- Properties of Adjoint Configurations [in order to distinguish from Direct configuration properties, a superscript † has been attached to each parameter name] …
- As listed in column 7 of our Table, the "spin" angular velocity of the adjoint equilibrium configuration has been determined from the vorticity of the direct configuration via the relation,
- As listed in column 10 of our Table, the ratio of the vorticity to the angular velocity in the adjoint equilibrium configuration has been determined from the same ratio in the direct configuration via the relation,
- As indicated, the value of the vorticity in the adjoint equilibrium configuration (column 9 of our table) has been determined from a product of and .
- As listed in column 8 of our table, the value of the parameter, , has been determined from the vorticity in the adjoint equilibrium configuration via the relation,
|
Table 1: Example Riemann S-type Ellipsoids |
|||||||||
|
Properties of |
Properties of |
||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| 0.90 | 0.795 | 1.14704 | 0.43181 | -0.86842 | -0.75709 | -0.43181 | -1.14704 | +2.30682 | -5.3422 |
| 0.641 | 1.13137 | 0.15077 | - 0.30322 | - 0.26801 | - 0.15077 | -1.13137 | 2.27531 | - 15.0913 | |
| 0.590 | 1.10661 | 0.06406 | -0.12883 | -0.11642 | -0.06406 | -1.10661 | +2.22552 | -34.7411 | |
| 0.564 | 1.09034 | 0.02033 | -0.04089 | -0.03750 | -0.02033 | -1.09034 | +2.19279 | -107.86 | |
| 0.538 | 1.07148 | - 0.02324 | +0.04674 | +0.04362 | +0.02324 | - 1.07148 | +2.15487 | +92.722 | |
| 0.487 | 1.02639 | - 0.10880 | +0.21881 | +0.21318 | +0.10880 | -1.02639 | +2.06418 | +18.972 | |
| 0.333 | 0.79257 | - 0.39224 | +0.78884 | +0.99529 | +0.39224 | -0.79257 | +1.59395 | +4.06370 | |
| 0.28 | 0.256 | 0.80944 | 0.03668 | -0.14127 | -0.17453 | -0.03668 | -0.80944 | +3.11750 | -84.992 |
| 0.245083 | 0.796512a | 0.0 | 0.0 | 0.0 | 0.0 | … | … | ||
| 0.231 | 0.77651 | - 0.04714 | +0.18156 | +0.23381 | +0.04714 | -0.77651 | +2.99067 | +63.442 | |
| 0.205 | 0.72853 | - 0.13511 | +0.52037 | +0.71427 | +0.13511 | -0.72853 | +2.80588 | +20.7674 | |
|
aAccording to Table IV (p. 103) of [EFE], the square of the angular velocity of this Jacobi ellipsoid is, ; from this value, we find that, . |
|||||||||
Our Parameter Determinations
The parameter values that have been posted above in our Table 1 are typically given with five digits of precision. This is because, as explained, the values were determined from the analytically determined values, and , that were provided by 📚 Ou (2006) with only five digit accuracy. Our Table 2 (shown immediately below) provides values of this same set of model parameters to better than eleven digits accuracy. We calculated these parameter values by following the steps detailed in earlier subsections of this chapter and, as a foundation, using double-precision versions of Numerical Recipes algorithms to evaluate the special functions, and . As an example, the above pair of brief tables titled, TEST (part 1) and TEST (part 2) detail all of the intermediate steps that were used in order to determine the high-precision parameter values specifically for the model having the axis-ratio pair . This table of higher precision parameter values was primarily generated in order to convince ourselves that we understood from first principles how to accurately determine the properties of Riemann S-type ellipsoids; the lower-precision parameter values that we derived from Ou's work provided a handy means of cross-checking these "first principles" determinations.
In generating our Table 2, we wondered what the approriate signs were of the various model parameters — especially when part of our objective is to distinguish between direct and adjunct configurations. We took the following approach: First we decided that the spin frequency of every direct configuration should be positive. (Evidently, Ou made this same choice.)
|
Table 2: Example Riemann S-type Ellipsoids (double-precision evaluation) |
|||||||||
|
Properties of |
Properties of |
||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| 0.90 | 0.795 | +1.147036091720 | +0.431809451699 | -0.868416786194 | -0.757096320116 | -0.431809460593 | -1.147036104571 | +2.306817054749 | -5.342210487323 |
| 0.641 | +1.131374738327 | +0.150771621841 | -0.303218483925 | -0.268008886644 | -0.150771621877 | -1.131374730590 | +2.275320291519 | -15.091170863305 | |
| 0.590 | +1.106612583610 | +0.064060198174 | -0.128832176328 | -0.116420305902 | -0.064060197762 | -1.106612576964 | +2.225520849228 | -34.741086358509 | |
| 0.564 | +1.090339840378 | +0.020334563779 | -0.040895067155 | -0.037506716440 | -0.020334563809 | -1.090339837153 | +2.192794561386 | -107.8358300897 | |
| 0.538 | +1.071485625744 | -0.023236834336 | +0.046731855720 | +0.043614077664 | +0.023236835120 | -1.071485656401 | +2.154876708984 | +92.735376233270 | |
| 0.487 | +1.026387311947 | -0.108799837242 | +0.218808561563 | +0.213183225210 | +0.108799835209 | -1.026387320039 | +2.064178943634 | +18.972261524065 | |
| 0.333 | +0.792566980901 | -0.392440787995 | +0.789242029190 | +0.995804846843 | +0.392440793882 | -0.792566979129 | +1.593940258026 | +4.061606964516 | |
| 0.74 | 0.692 | +1.132148956838 | +0.385991660900 | -0.807244181633 | -0.713019398562 | -0.385991654519 | -1.132148989537 | 2.367721319199 | -6.134125500116 |
| 0.41 | 0.385 | +0.971082162758 | +0.141593941719 | -0.403404593468 | -0.415417564427 | -0.141593939418 | -0.971082191477 | 2.766636848450 | -19.539231537777 |
| 0.333 | +0.929630138695 | +0.003311666790 | -0.009435019456 | -0.010149218281 | -0.003311666699 | -0.929630099681 | +2.648538827896 | -799.7601146950 | |
| 0.28 | 0.256 | +0.809436834686 | +0.036676037913 | -0.141255140305 | -0.174510396110 | -0.036676038521 | -0.809436833116 | +3.117488145828 | -85.000678306244 |
| 0.245083 | 0.796512a | 0.0 | 0.0 | 0.0 | 0.0 | … | … | ||
| 0.231 | +0.776514825339 | -0.047142035397 | +0.181564182043 | +0.233819345828 | +0.047142037070 | -0.776514835457 | +2.990691423416 | +63.440011724689 | |
| 0.205 | +0.728526018042 | -0.135108121071 | +0.520359277725 | +0.714263156392 | +0.135108125079 | -0.728526039364 | +2.805866003036 | +20.767558718483 | |
|
aAccording to Table IV (p. 103) of [EFE], the square of the angular velocity of this Jacobi ellipsoid is, ; from this value, we find that, . |
|||||||||
| Figure 2: EFE Diagram |
In the context of our broad discussion of ellipsoidal figures of equilibrium, the label "EFE Diagram" refers to a two-dimensional parameter space defined by the pair of axis ratios (b/a, c/a), usually covering the ranges, 0 ≤ b/a ≤ 1 and 0 ≤ c/a ≤ 1. The classic/original version of this diagram appears as Figure 2 on p. 902 of 📚 Chandrasekhar (1965; XXV); a somewhat less cluttered version appears on p. 147 of Chandrasekhar's [EFE]. The version of the EFE Diagram shown here, on the left, highlights four model sequences, all of which also can be found in the original version:
Riemann S-type ellipsoids all lie between or on the two (self-adjoint) curves marked "X = -1" and "X = +1" in the EFE Diagram. The yellow circular markers in the diagram shown here, on the left, identify four Riemann S-type ellipsoids that were examined by Ou (2006) and that we have also chosen to use as examples. |
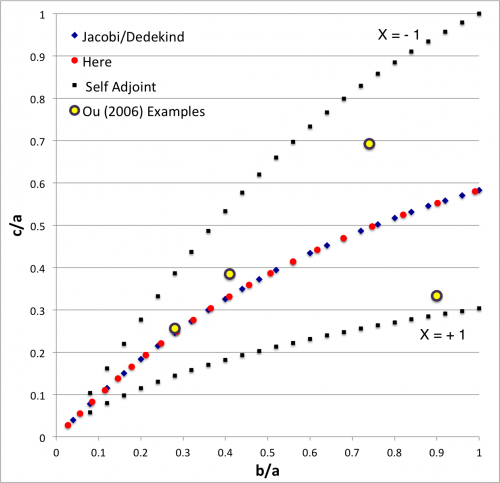 |
| Self-Adjoint Sequences EFE, §48, p. 142, Table VI Also, Howard Cohl's High-Resolution Analysis |
c/a for Upper (x = - 1) Sequence c/a for Lower (x = + 1) Sequence
b/a (EFE) (20-digit accuracy) (EFE) (20-digit accuracy)
0.00 0.00000 0.00000000000000000000 0.00000 0.000000000000000000000
0.04 --- 0.04812224688754297818 --- 0.032492366749482199925
0.08 0.10361 0.10361306225462674898 0.057817 0.057816723024001224133
0.12 0.16154 0.16153789497880627606 0.079299 0.079298698625164323530
0.16 0.21970 0.21969876513711574739 0.098178 0.098178582821665570336
0.20 0.27691 0.27691183106981782343 0.11513 0.11512631936916250684
0.24 0.33250 0.33250375904983621093 0.13056 0.13056017471495792387
0.28 0.38609 0.38608942382754657558 0.14476 0.14476444864794971656
0.32 0.43746 0.43745820820586512706 0.15794 0.15794374720008968932
0.36 0.48651 0.48651009591845463512 0.17025 0.17025155740243264509
0.40 0.53322 0.53321717007090044978 0.18181 0.18180672031800805031
0.44 0.57760 0.57759916496531807675 0.19270 0.19270358265482766408
0.48 0.61971 0.61970731624526462073 0.20302 0.20301858308989486955
0.52 0.65961 0.65961338021128620371 0.21281 0.21281470455368433422
0.56 0.69740 0.69740201597965416041 0.22214 0.22214458680677346510
0.60 0.73316 0.73316543250962834935 0.23105 0.23105276438034978438
0.64 0.76700 0.76699960292399202953 0.23958 0.23957731445406474795
0.68 0.79900 0.79900158609578752317 0.24775 0.24775109537636838357
0.72 0.82927 0.82926764261302051281 0.25560 0.25560269426540122707
0.76 0.85789 0.85789192689326638880 0.26316 0.26315716347079152387
0.80 0.88497 0.88496560014936540261 0.27044 0.27043660093734799732
0.84 0.91058 0.91057625192549140531 0.27746 0.27746061325324716171
0.88 0.93481 0.93480754802412975193 0.28425 0.28424668922671777898
0.92 0.95774 0.95773904411679071746 0.29081 0.29081050432029451542
0.96 0.97945 0.97944611989047804643 0.29714 0.29716617101118183175
1.00 1.00000 1.00000000000000000000 0.30333 0.30332644640104007578
|
Feeding a 3D Animation
Initial Thoughts
Let's examine the elliptical trajectory of a Lagrangian particle that is moving in the equatorial plane of a Riemann S-Type ellipsoid. As viewed in a frame that is spinning about the Z-axis at angular frequency, , the trajectory is defined by,
|
|
|
|
where . (The surface of the relevant ellipsoid is associated with the value, .)
Let's choose a pair of axis ratios — for example, and — then, from Table 1 of our above discussion, draw the associated value of either or that corresponds to the Jacobi-like equilibrium configuration — in this example, and . Then, for any point inside of the ellipsoid, the fluid's velocity components (as viewed from the rotating frame of reference) are,
|
|
and, |
|
Alternatively, we have,
|
|
and, |
|
Now, each Lagrangian fluid element's motion is oscillatory in both the and coordinate directions. So let's see how this plays out. Suppose,
|
|
and, |
|
Then,
|
|
and, |
|
Hence our functional representation of the time-dependent behavior of both and works perfectly if, for each orbit inside of or on the surface of the configuration, we set and if the ratio . Hooray!
Preferred Normalizations
Let's do this again, assuming that and both have units of length and that has the unit of time. Then, let's use to normalize lengths and use to normalize time. We therefore have,
|
|
and, |
|
|
NOTE: When implementing in an xml-based COLLADA (3D animation) file, we associate with . Hence we can everywhere replace with (in radians) or (in degrees) .
|
Next, let's normalize the velocities such that and the total mass, , are both assumed to be the same in every examined Riemann ellipsoid. In particular, we will normalize to,
|
|
|
|
|
|
in which case we have,
|
|
and, |
|
Finally, setting, means,
|
|
and, |
|
Example Mach Surface
Let's try to plot the "Mach surface" for the example model, b41c385, referenced below. Its relevant parameter values are,
Hence, if we set a = 1 then we have,
| and | ||||||
Borrowing from an accompanying discussion, we have the following example data set.
| Direct | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| n | Axisymmetric | b41c385 | Surface | |V| = 0.1 | ||||||
| x0 | y0 | y = 0.41 × y0 | Vx | Vy | |V| | factor | x | y | ||
| 1 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | -0.0606 | 0.0606 | --- | --- | --- | |
| 2 | 0.9921 | -0.1253 | -0.0514 | -0.0185 | -0.0601 | 0.0629 | --- | --- | --- | |
| 3 | 0.9686 | -0.2487 | -0.1020 | -0.0368 | -0.0587 | 0.0693 | --- | --- | --- | |
| 4 | 0.9298 | -0.3681 | -0.1509 | -0.0544 | -0.0563 | 0.0783 | --- | --- | --- | |
| 5 | 0.8763 | -0.4818 | -0.1975 | -0.0712 | -0.0531 | 0.0888 | --- | --- | --- | |
| 6 | 0.8090 | -0.5878 | -0.2410 | -0.0869 | -0.0490 | 0.0998 | 1.002 | 0.8090 | -0.2410 | |
| 7 | 0.7290 | -0.6845 | -0.2807 | -0.1012 | -0.0442 | 0.1104 | 0.9058 | 0.6603 | -0.2543 | |
| 8 | 0.6374 | -0.7705 | -0.3159 | -0.1139 | -0.0386 | 0.1203 | 0.8313 | 0.5298 | -0.2626 | |
| 9 | 0.5358 | -0.8443 | -0.3462 | -0.1248 | -0.0325 | 0.1290 | 0.7752 | 0.4153 | -0.2684 | |
| 10 | 0.4258 | -0.9048 | -0.3710 | -0.1337 | -0.0258 | 0.1362 | 0.7342 | 0.3126 | -0.2724 | |
| 11 | 0.3090 | -0.9511 | -0.3899 | -0.1406 | -0.0187 | 0.1418 | 0.7052 | 0.2179 | -0.2750 | |
| 12 | 0.1874 | -0.9823 | -0.4027 | -0.1452 | -0.0114 | 0.1456 | 0.6868 | 0.1287 | -0.2766 | |
| 13 | 0.0628 | -0.9980 | -0.4092 | -0.1475 | -0.0038 | 0.1476 | 0.6775 | 0.0425 | -0.2772 | |
In an accompanying discussion of axisymmetric configurations, we have recognized that, at any point inside the configuration, the square of the sound speed is given approximately by the enthalpy where,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Drawing from equation (7) of 📚 Ou (2006) and from a separate discussion of gravitational potential of homogeneous ellipsoids, we see that the effective potential is,
where,
|
|
|
|
Setting , let's use the test case from above — that is, (b/a, c/a) = (0.9, 0.641) — and see if we get the same value of the Bernoulli constant on the surface at each of the three principal axes. First, let's set x = y = 0 and z = c. In this case we find,
|
|
|
|
Next, let's set y = z = 0 and x = 1. In this case,
|
|
|
|
S-Type Ellipsoid Example b41c385
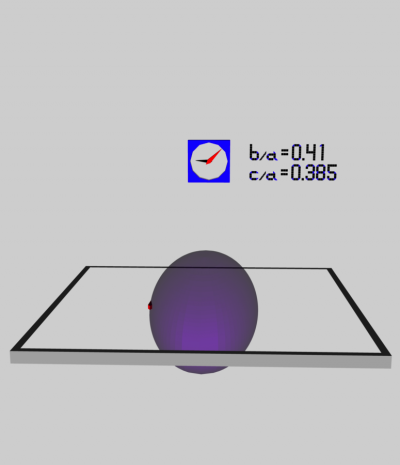
The EFE model that we chose to use in our first successful construction of a COLLADA-based, 3D and interactive animation had the following properties (model selected from the above table):
Figure 1 displays a pair of still-frame images of this (purple) ellipsoidal configuration after the ellipsoid has completed precisely five (counter-clockwise) spin cycles. (The snapshots have been taken at the same point in time, but from two different "camera" viewing angles.) The cycle of the "wall mounted" clock is based on the fundamental, EFE-adopted frequency of [π G ρ]½. In the left-hand image (labeled Figure 1a), the time on the clock appears to be about 9:08. This means that as the ellipsoid has completed five spin cycles, the clock has completed approximately [9 + 8/60] ≈ 9.13 cycles. In other words, the ratio (ellipsoid-to-clock) of these two frequencies is,
|
|
|
|
This matches the tabulated value of presented above. Now, let's examine the motion of an example Lagrangian fluid element, which has been marked in the 3D scene by a red "arrow" riding in the equatorial plane and along the surface of the (purple) ellipsoidal figure. At time zero, the fluid marker was placed at the end of the longest axis of the ellipsoid that was nearest the "wall clock"; then, as time progressed and the ellipsoidal figure turned counter-clockwise, the fluid marker moved clockwise and completed less than one full "orbit" in the same time that the ellipsoidal figure completed five full spin cycles. In the right-hand image (labeled Figure 1b), we can see that relative to the ellipsoidal figure, the fluid marker has moved through approximately three-quarters of its assigned elliptical "orbit"; let's say, 73% of one full cycle. This means that the ratio of the Lagrangian fluid element's orbital frequency to the frequency of the wall-clock is,
|
|
|
|
This matches the tabulated value of presented above.
See Also
- Discussion of Ou's Riemann-Like Ellipsoids
- Riemann Meets COLLADA & Oculus Rift S
- Virtual Reality and 3D Printing
- Success Importing Animated Scene into Oculus Rift S
- Carefully (Re)Build Riemann Type S Ellipsoids Inside Oculus Rift Environment: Example (b/a, c/a) = (0.41, 0.385)
- Other Example S-type Riemann Ellipsoids:
Chandrasekhar's Detailed Analysis
- Bernhard Riemann (1876) Gesammelte Mathematische Werke und Wissenschaftlicher, especially Chapter X (p. 168) titled (something along the following line), "A Contribution to Research on Rotating Ellipsoidal Fluids"
- S. Chandrasekhar (1965), ApJ, 142, 890 - 961. The Equilibrum and the Stability of the Riemann Ellipsoids. I. — This work is referenced as Paper XXV in EFE and focuses on S-type Riemann ellipsoids.
- S. Chandrasekhar (1966), ApJ, 145, 842 - 877. The Equilibrum and the Stability of the Riemann Ellipsoids. II. — This work is referenced as Paper XXVIII in EFE and focuses on Riemann ellipsoids of Types I, II and III.
Finite-Amplitude Oscillations
- L. F. Rossner (1967), ApJ, 149, 145. The Finite-Amplitude Oscillations of the Maclaurin Spheroids — This work is referenced as Paper XXXVIII in EFE.
- M. Fujimoto (1968), ApJ, 152, 523. Gravitational Collapse of Rotating Gaseous Ellipsoids
- T. T. Chia & S. Y. Pung (1995), Astrophysics and Space Science, 229, issue 2, 215 - 233. Effects of Variations of Parallel Angular Velocity and Vorticity on the Oscillations of Compressible Homogeneous Rotating Ellipsoids
- T. T. Chia & S. Y. Pung (1997), Astrophysics and Space Science, 254, 269 - 294. Dynamical Behaviour of Compressible Homogeneous Uniformly Rotating Ellipsoids with Nonparallel Angular Velocity and Vorticity
In the Context of Galaxy Disks
- C. Hunter (1970), ApJ, 162, 97 - 103. The Disklike Riemann Ellipsoids.
Other
Footnotes
- In EFE this equation is written in terms of a variable instead of as defined here. The two variables are related to one another straightforwardly through the expression, .
- Throughout EFE, Chandrasekhar adopts a sign convention for the scalar gravitational potential that is opposite to the sign convention being used here.

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |