Appendix/Ramblings/ForCohlHoward
Discussion Regarding Stability Studies Performed by Lebovitz
Motivation
These discussions began in late 2021, when Howard Cohl asked if I would be interested in working with him on establishing a better understanding of the stability of Riemann S-Type Ellipsoids. This discussion relates directly to our study of the work by 📚 N. R. Lebovitz, & A. Lifschitz (1996, ApJ, Vol. 458, pp. 699 - 713).
We are motivated to pursue this discussion, in part, because our own research group at LSU has previously carried out some nonlinear dynamical simulations that relate to this topic. See …
- YouTube Simulation that draws from the following ApJ publication.
-
Relevant Publication: 📚 S. Ou, J. E. Tohline, & P. M. Motl (2007, ApJ, Vol. 665, pp. 1074 - 1083), titled, Further Evidence for an Elliptical Instability in Rotating Fluid Bars and Ellipsoidal Stars.
Publication Abstract
Using a three-dimensional nonlinear hydrodynamic code, we examine the dynamical stability of more than 20 self-gravitating, compressible, ellipsoidal fluid configurations that initially have the same velocity structure as Riemann S-type ellipsoids. Our focus is on adjoint configurations, in which internal fluid motions dominate over the collective spin of the ellipsoidal figure; Dedekind-like configurations are among this group. We find that, although some models are stable and some are moderately unstable, the majority are violently unstable toward the development of m=1, m=3, and higher-order azimuthal distortions that destroy the coherent, m=2 barlike structure of the initial ellipsoidal configuration on a dynamical timescale. The parameter regime over which our models are found to be unstable generally corresponds with the regime over which incompressible Riemann S-type ellipsoids have been found to be susceptible to an elliptical strain instability. We therefore suspect that an elliptical instability is responsible for the destruction of our compressible analogs of Riemann ellipsoids. The existence of the elliptical instability raises concerns regarding the final fate of neutron stars that encounter the secular bar-mode instability and regarding the spectrum of gravitational waves that will be radiated from such systems.

Initial frame of a YouTube animation that shows one model's evolution
Understanding the Dimensionality of EFE Index Symbols
Howard put together a Mathematica script intended to provide — for any specification of the semi-axis length triplet — very high-precision, numerical evaluations of any of the index symbols, and as defined by Eqs. (103 - 104) in §21 of [EFE]. Originally I suggested that, without loss of generality, he should only need to specify the pair of length ratios, . In response, Howard pointed out that evaluation of all but a few of the lowest-numbered index symbols — as defined by [EFE] — does explicitly depend on specification of (various powers of) the semi-axis length, .
Joel's response: Howard is correct! He should leave the explicit dependence of — to various powers — in his Mathematica notebook's determination of all the EFE index symbols.
Instead, what we should expect is that the evaluation of various physically relevant parameters will produce results that are independent of the semi-axis length, ; these evaluations should involve combining various index symbols in such a way that the dependence on disappears. Consider, for example, our accompanying discussion (click to see relevant expressions) of the virial-equilibrium-based determination of the frequency ratio, , in equilibrium S-Type Riemann Ellipsoids. Although most of the required index symbols, and , are dimensionless parameters, the index symbol has the unit of inverse-length-squared. Notice, however, that when appears along with any of these other dimensionless parameters in the definition of , it is accompanied by an extra "length-squared" factor, such as . Hence, although I strongly agree that Howard should continue to include various powers of (etc.) in his Mathematica notebook expressions, I suspect that, without loss of generality, in the end we will always be able to set and only need to specify the pair of length ratios, .
Evaluation of Index Symbols
Three Lowest-Order Expressions
In our accompanying derivation of expressions for the three lowest-order index symbols , we have used subscripts instead of in order to identify which associated semi-axis length is (largest, medium-length, smallest). We have derived the following expressions:
|
The corresponding expressions that appear in Howard's Mathematica notebook are:
|
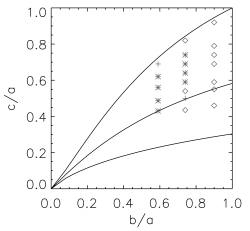
With a little study it should be clear that our derived expressions for precisely match Howard's Mathematica-notebook expressions when , , and , that is, in all cases for which . But there will be models to consider (for example, in the uppermost region of the so-called "horn-shaped" region for S-Type Riemann Ellipsoids) for which , in which case care must be taken in assigning the proper expressions to and . Similarly note that most of the Riemann models of Type I, II, and III — see, for example, Figure 16 (p. 161) in Chapter 7 of [EFE] — have either or .
Determination of Higher-Order Expressions
Howard's Mathematica notebook performs brute-force integrations to evaluate various higher-order index-symbol expressions. Why doesn't he instead use recurrence relations, which point back to the elliptic-integral-based expressions for ? Specifically …
|
Index-Symbol Recurrence Relations |
||
|
|
|
|
|
[EFE], §21, p. 54, Eq. (105) |
||
|
|
|
|
|
[EFE], §21, p. 54, Eq. (106) |
||
|
|
|
|
|
[EFE], §21, p. 54, Eq. (107) |
||
For example, setting and in the third of these expressions gives,
|
|
|
|
|
|
|
|
|
|
|
|
and, from the first of the relations,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Also, consider using the set of relations labeled "LEMMA 7" on p. 54 of [EFE].
Example Test Evaluations
Some of Howard's 20-digit-precision evaluations of various index symbols have been recorded, for comparison with our separate lower-precision evaluations, as follows:
- Values of are recorded for a model with in the table titled, TEST (part 1), near the top of our chapter on Riemann S-Type ellipsoids.
- Values of are recorded for a model with in the table titled, TEST (part 2) in our chapter on Riemann S-Type ellipsoids.
Figures circa Year 2000
Approximately four years after 📚 Lebovitz & Lifschitz (1996) was published, Norman Lebovitz gave a copy of his stability-analysis (FORTRAN) code to Howard Cohl. Using this code, Howard was able to generate a large set of growth-rate data that essentially allowed him to reproduce Figure 2b from 📚 Lebovitz & Lifschitz (1996).
Image i3.png
Howard's plot of this data — his image i3.png — is shown immediately below; the abscissa is and the ordinate is .
| Howard's "i3.png" image |  |
|
Compare with Figure 2b of 📚 N. R. Lebovitz, & A. Lifschitz (1996, ApJ, Vol. 458, pp. 699 - 713) |
Image i5.png
In an effort to better examine growth-rate trends in the lower-left quadrant of this 📚 Lebovitz & Lifschitz (1996) figure, Howard plotted the same set of stability-analysis data on an axis pair where the abscissa is still , but where, for each value of , the ordinate extends from the lower self-adjoint sequence to the upper self-adjoint sequence — labeled, respectively, and in the classic EFE diagram (EFE, §49, p. 147, Fig. 15 or, see our accompanying discussion). This is displayed immediately below as Howard's "i5.png" image.
| Howard's "i5.png" image |  |
|
Notice … |
In generating his "i5.png" image, precisely how did Howard "stretch" the ordinate from (as used in his "i3.png" image) to an ordinate ranging from the lower to the upper self-adjoint sequences? Drawing from 📚 Lebovitz & Lifschitz (1996) I presume that, for a given point in the EFE diagram , Howard used the expression,
|
|
|
|
|
📚 Lebovitz & Lifschitz (1996), §2, p. 701, Eq. (8) |
||
where,
|
|
|
|
|
📚 Lebovitz & Lifschitz (1996), §2, p. 701, Eq. (6) |
||
Then I presume that the ordinate, — which runs from zero to unity in the "i5.png" image — is determined from the expression,
|
|
|
|
Is this the way Howard generated "i5.png"?
|
In an email dated 26 January 2022, Howard provided the following answer to this question —
|
Image i4.png
Howard's "i4.png" image, immediately below, presents a magnification of the upper-right-hand portion (identified, by hand, as the "E-group") of his "i5.png" image. The abscissa spans the parameter range, while the ordinate spans the parameter range, .
| Howard's "i4.png" image |  |
|
Notice … |
Summary
Howard is interested in understanding — in greater detail than appears in 📚 Lebovitz & Lifschitz (1996) — what gives rise to, and what is the extent of these various bands of instability in the classic EFE diagram. Explicit comments/questions:
- Notice in "i4.png" that the bands labeled E4, E6, and E8 appear to extend all the way to, and intersect, the Maclaurin spheroid sequence.
Self-Adjoint Sequences
|
In an email dated 26 January 2022, Howard asked, "Do you have analytic curves for the lower and upper self-adjoint sequences? Otherwise, do you have very accurate data for the lower and upper self-adjoint sequences?" |
On the same day, I sent the following response to Howard:
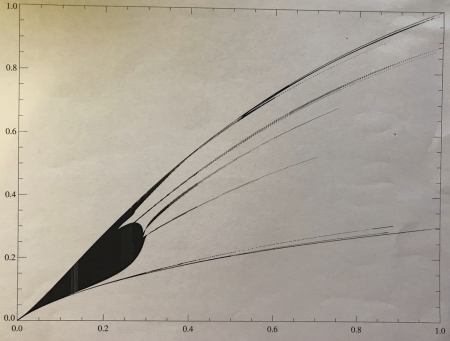
I have added a subsection to my online chapter discussion of 📚 Lebovitz & Lifschitz (1996) in which I derive an expression whose solution/root should map out the **upper** boundary (x = -1) of the horned-shape region. Click here to see the entire derivation; this derivation ends with the following recommended strategy:
|
STRATEGY for finding the locus of points that define the upper boundary of the horned-shape region … Set , and pick a value for ; then, using an iterative technique, vary until the following expression is satisfied:
Choose another value of , then iterate again to find the value of that corresponds to this new, chosen value of . Repeat! |
Related remarks:
- I have not actually plugged in numbers -- that is, (b,c) pairs -- to see if it works, but I am pretty confident in the result because the derivation was pretty straightforward. Would you mind trying it out for me, since you have working elliptic integral routines?
- It would be wise to start by trying to duplicate -- then improve upon -- the set of (b, c) coordinate-pairs that were derived by Chandrasekhar and presented in EFE Table VI (section 48, p. 142).
- Shortly, I will derive the complementary expression that maps out the "lower" boundary (x = +1).
On 27 January 2022, Joel added a subsection to the online chapter discussion of 📚 Lebovitz & Lifschitz (1996) in which he derives an expression whose solution/root should map out the **lower** boundary (x = +1) of the horned-shape region. Click here to see the entire derivation; this derivation ends with the following recommended strategy:
|
STRATEGY for finding the locus of points that define the lower boundary of the horned-shape region … Set , and pick a value for ; then, using an iterative technique, vary until the following expression is satisfied:
Choose another value of , then iterate again to find the value of that corresponds to this new, chosen value of . Repeat! |
|
Upper (USA) and Lower (LSA) Self-Adjoint
(Howard's Compact Expressions Plus Plot 1/28/2022) |
COLLADA 3D Animations
|
|
Riemann Type I Ellipsoids
Excerpts From Various Lebovitz Publications Regarding Stability Studies
Why is Lagrangian Perturbation Method Preferred?
|
"… a preliminary version — see Lebovitz (1987) — of the methods of the present paper [have shown that] … they enjoy certain advantages over other methods that have been employed in related problems (like Cartan's method and the virial method)." |
|
— Drawn from the last paragraph on p. 222 of 📚 Lebovitz (1989a). |
|
[EFE] "… utilizes the virial equations, which require a separate derivation for modes associated with ellipsoidal harmonics of various orders; it is accordingly restricted to those of low order (at most four).." |
|
— Drawn from the first paragraph of §1 (p. 225) in 📚 Lebovitz (1989b). |
Contrast with Radial Pulsation Eigenvectors
|
Schwarzschild's 1941 Analysis of Radial Oscillations in n = 3 Polytropes |
|||||
|
|||||
By contrast, in LL96, "the basic equation" appears in the form,
|
|
||
|
LL96, §3.1, p. 701, Eq. (10) |
||
This means that the matrix operators, & , found in 📚 Lebovitz (1989b) and re-derived herein, have simply been renamed in LL96. That is to say, in LL96,
|
|
and, |
|
where,
|
|
||
|
LL96, §3.1, p. 703, Eq. (17) |
||
Determining Oscillation Frequencies and Growthrates
6 February 2022: Howard asked me to clarify how the solution to the "basic linear perturbation equation" provides values for the growth rate of an unstable mode.
Spherically Symmetric Situations
In a separate chapter I have explained how the eigenvalue problem is set up for one-dimensional (spherically symmetric) configurations. Traditionally, the assumption is that you are starting from an equilibrium configuration for which you know how pressure , density , and radius vary with mass shell , everywhere inside (and on the surface) of the configuration. As the following three equations illustrate, you "perturb" the configuration by assuming that there are low-amplitude fluctuations to each variable, namely, , , and , and that these fluctuations each vary with spatial location — that is, with mass shell — inside the configuration as well a s with time.
|
|
|
|
|
|
|
|
|
|
|
|
The convention is to assume, as shown, that the spatial portion of the variation can be separated from the time-dependent portion, and that the time-dependent portion is of the form, . Then, when these quantities are introduced into the governing linear perturbation equation, any term involving one partial time-derivative — for example, — will generate a term of the form, ; while any term involving a second partial time-derivative will generate a term of the form, . Usually, every term in the governing linear perturbation equation will contain a factor of , so it can be divided out. This leaves you with a perturbation equation that has no explicit time dependence; it only contains spatial derivatives of variables along with a few or terms.
The very nature of an eigenvalue problem is to see if the perturbation equation can be solved to give you the square of the characteristic oscillation frequency, for one (or, hopefully more) mode along with a specification of how the spatial part of the mode varies with location inside the configuration. If is positive, then the exponent of is imaginary, which identifies a periodic oscillation; if is negative, then the exponent of is real, which identifies an exponentially growing (or, formally as well, decaying) mode.
Riemann S-Type Ellipsoids
Notice that Eq. (25) of L89a assumes that the three-dimensional, time-dependent perturbation, , of the Riemann S-Type ellipsoid is of the form,
|
|
|
|
Notice that time-dependence and spatial-dependence have been separated. And I presume that the time-dependent coefficients, , will include factors of . Notice as well that, in LL96, "the basic equation" appears in the form,
|
|
||
|
LL96, §3.1, p. 701, Eq. (10) |
||
The subscript means that the perturbation will be twice differentiated in time, while the subscript means a single time-differentiation. The oscillation frequency (or growth rate) probably will appear in the basic perturbation equation via these two terms.
Index Symbols for Type I Riemann Ellipsoids
2 March 2022: Joel requests Howard's assistance in verifying the correct expressions to use for the index symbols, , when constructing "Type I" Riemann ellipsoids.
As has been summarized above, when I have derived expressions for the three lowest-order index symbols, I have used instead of as the subscript notation. In the context of our discussion of Riemann S-type ellipsoids, it is usually the case that is the longest semi-axis and is the shortest semi-axis, so we can adopt the association, . This is consistent with the set of expressions for , , and , that Howard has defined inside of his Mathematica notebook, namely …
|
But I am also interested in developing a better understanding of the structural properties of Type I Riemann Ellipsoids. For these systems, it is the case that is the longest semi-axis and is the shortest semi-axis, so we should adopt the association, . In STEP #2 of the chapter that I am writing about Type I Riemann Ellipsoids, I claim that the correct expressions for the three lowest-order index symbols are …
|
|
|
|
|
|
|
|
|
|
|
|
where, the arguments of the incomplete elliptic integrals are,
|
|
and |
|
I would like to know if Howard agrees with this claim. In particular, I would like to know what values of he obtains using Mathematica's tools, for the following pairs of model axis ratios.
|
Example Models Drawn Primarily† from Table 4 (p. 858) of 📚 Chandrasekhar (1966; XXVIII) |
||||
| Howard Cohl's 20-Digit Precision Evaluation of Index Symbols | ||||
| A1 | A2 | A3 | ||
| 1.05263 | 0.41667 | 0.43008853859109863146 | 0.40190463270335853286 | 1.1680068287055428357 |
| 1.25000 | 0.50000 | 0.50824409128926609544 | 0.37944175746381924039 | 1.1123141512469146642 |
| 1.44065 | 0.49273 | 0.52404662956445493304 | 0.32351600902859843592 | 1.1524373614069466310 |
| 1.66666 | 0.33333 | 0.41804279087942201679 | 0.20718018294728778618 | 1.3747770261732901970 |
| 1.36444 | 0.09518 | 0.14378468450707924448 | 0.091526900363135453419 | 1.7646884151297853021 |
| 1.69351 | 0.11813 | 0.18177227461540501422 | 0.084646944102441440238 | 1.7335807812821535455 |
| 1.52303 | 0.05315 | 0.085943612594485367787 | 0.046184257303756474717 | 1.8678721301017581575 |
| 1.78590 | 0.06233 | 0.10259594310295396216 | 0.043583894016884923661 | 1.8538201628801611142 |
| 1.2500 | 0.4703 | 0.48955940032702523984 | 0.36486593343389634429 | 1.1455746662390784159 |
|
†NOTE: The model whose axis-ratios are highlighted with a yellow background has been drawn from Table 6a (p. 871) of 📚 Chandrasekhar (1966; XXVIII) |
||||
If you want to know how I derived the relevant index-symbol expressions, go to my MediaWiki chapter that discusses The Gravitational Potential (Ai coefficients) in the context of Ellipsoidal & Ellipsoidal-Like equilibrium structures.
|
More specifically, go to the subsection of this chapter titled, "Derivation of Expressions for Ai," where I evaluate . These expressions will always remain the same. Then the question is, for your specific problem of interest, which ellipsoidal axis or is the "largest, medium-sized, or smallest"? When considering Riemann Type-I Ellipsoids, is the largest axis, so ; is the smallest axis, so ; and is the medium-sized axis, so .
Considering Utility of Finite-Element Techniques
Joel's Opening Comments
Among the introductory chapters of our MediaWiki-based discussion of Self-Gravitating Fluids, you will find a formal list of the relevant "Principal Governing Equations" and an accompanying discussion of, for example, the Euler equation. Here, we pull from that discussion the so-called,
which contains the divergence of the "dyadic product" or "outer product" of the vector momentum density and the velocity vector, and is sometimes written as, . How do we rewrite this continuum equation in a discrete form that will allow us (using digital computers) to accurately integrate this equation — in tandem with the other "Principal Governing Equations" — to determine how the fluid momentum at every point in space evolves in time? Answering this question is a particularly challenging task because the so-called advection term on the left-hand-side is inherently nonlinear in the velocity.
Over the years, applied mathematicians — including, for example, engineers, physicists, astronomers, aerodynamicists — have devised a large array of schemes, the most popular falling under one of the following three broad (Wikipedia-acknowledged!) categories:
- Finite-Difference Method (FDM)
- Finite-Volume Method (FVM) Our category of choice, historically (see immediately below)
- Finite-Element Method (FEM)
When I googled "finite element vs finite difference " on 13 October 2022, I was pointed to, for example,
- Comparison of Finite-Element and Finite-Difference Methods
- What's the Difference Between FEM, FDM, and FVM?
Our Choice, Historically
Over the past four decades, the nonrelativistic fluid simulations that have been performed by LSU's astrophysics group have been carried out using various renditions of an explicit Finite-Volume Method. The explicit FVM method was chosen primarily because …
- It was the method to which I was introduced by my doctoral dissertation advisors, Peter Bodenheimer and David Black, that was considered appropriate to the type of fluid-flows problems that were the focus of my dissertation research. Note that Bodenheimer is the first author of the book that is referenced above as BLRY07.
- Time-integration is fairly straightforward because all terms (except the time derivative) are specified entirely in terms of the current (as opposed to advanced) time.
- The nonlinear advection term on the LHS is written in a way that guarantees global momentum conservation, if the source terms on the RHS of the Euler equation sum to zero.
- The amount of computer time that is required to take each step forward in time is typically much smaller when using an explicit as opposed to implicit integration scheme.
A major disadvantage of our decades-old, explicit-FVM approach is that, in order for the scheme to be numerically stable, roughly speaking each integration time-step must be smaller than the smallest value of the ratio, , as determined across the entire grid, where is the grid spacing and is the fluid sound-speed. (Note that is essentially the sound-crossing time across the smallest grid cell.) This constraint on the integration time-step is computationally burdensome when attempting to employ a high-resolution (small ) grid and/or when attempting to model environments where the fluid is relatively hot and therefore characterized by a high sound speed. Even worse, it is impossible to model the evolution of incompressible fluids using an explicit-FVM scheme because, in effect in such fluids, sound travels at an infinite speed; that is, so goes to zero.
Quandary
Because we have chosen over the past four decades to employ an explicit-FVM approach in our examination of the stability of rotating, self-gravitating fluids, we have been constrained to examine the behavior of compressible rather than incompressible fluids. This is perfectly acceptable — and even desirable — in the context of studies of star-formation, for example, because we are confident that star-forming gas clouds and young protostars are composed of fluids that obey compressible equations of state. But it is difficult to critique the validity — and therefore relevance — of the results of such compressible-fluid simulations because the published literature contains virtually no linear-stability analyses of compressible fluid systems against which our nonlinear simulations can be compared.
On the other hand, as Chandrasekhar details in EFE, the literature is packed full of studies that have quantitatively assessed the relative stability of rotating, self-gravitating, incompressible fluid systems. (And, associated with the arrival of Stephen Sorokanich at NIST, we expect this literature to expand significantly.) So, the validity — and relevance — of our numerical simulations would be on a much firmer foundation if we had the ability to model the evolution of incompressible fluid systems. As an additional reward, a numerical simulation tool of this type would allow us to follow the nonlinear development of instabilities (in all Riemann ellipsoids, for example) whose onset has been predicted only from linear stability analyses.
Perhaps We Should Consider the FEM
Although I have had virtually no experience developing or using numerical algorithms that fall into the category of the Finite-Element Method (FEM), it is my understanding that such algorithms have the following features:
- They can be used to follow the evolution of incompressible — and, for example, uniform-density — fluid systems.
- They generally (always?) incorporate an implicit time-integration scheme in which case time steps are not constrained by — and can be much larger than — the often severely limiting sound-crossing times encountered in explicit FVM schemes.
- They are particularly good at identifying surfaces and modeling the time-evolution of surface distortions.
If you (Howard) and Sorokanich decide to build a hydro-code based on the Finite-Element Method, a potentially helpful reference is:
D. L. Meier (1999)
Multidimensional Astrophysical Structural and Dynamical Analysis.
I. Development of a Nonlinear Finite Element Approach
The Astrophysical Journal, Vol. 518, pp. 788 - 813
I interacted with David Meier at a couple of different meetings back at the time he was developing this FEM algorithm. I'm not sure what astrophysics problems he tackled with this code or, ultimately, what he did with it; for example, I have never seen "the second paper in this series" to which he refers in the abstract.
In the context of our examination of the stability of Riemann ellipsoids, an FEM might permit us to reduce the dimensionality of the problem. For example, ignore details associated with the interior of the 3D configuration and focus on modeling the distortion of its 2D surface.
We might even be able to model (for the first time!) the topological transformation that is experienced by the surface when a rapidly spinning, incompressible ellipsoid fissions into a pair of disconnected tear-drop shaped objects in orbit about one another. See, for example, the dissertation research of Shawn W. Walker (2007) (LSU Mathematics & CCT), or more recent papers that Walker has coauthored with his dissertation advisor, Ricardo H. Nochetto (U. Maryland, Mathematics).
Question Regarding Pressure-Poisson Equation
|
In an email dated 07 January 2023, Howard asked, "Do you think the pressure Poisson formulation of the Euler equations coupled with a 3D Poisson solver for gravity and evolution of the momentum equation might be our best strategy to evolve unstable Riemann S-type ellipsoids? We’ve already identified two different pieces of software (Fenics and COMSOL) which look like they might have this ability using finite-element. We also now have access to software which should be able to build good grids for FEM. Thanks! " |
Joel's response (11 January 2023) …
Your suggested "coupled Poisson formulation" sounds like a smart way to proceed. Note, however, that I say this with limited authority; I have never written a code to solve the Euler equations that is based on a pressure-Poisson formulation. My confidence in offering support for this approach comes from the following historical note.
In the early 1990s, in collaboration with Priya Vashishta, I helped the LSU Physics & Astronomy department secure approximately $0.8 million from the Louisiana Board of Regents to purchase an 8K-node SIMD architecture MasPar MP1. As you know, our astrophysics group developed a 3D Poisson solver that was extraordinally well suited to the 8K-node hardware layout of the MasPar. Around the same time that we received this state funding, I heard that the U.S. Department of Energy (DOE) was expecting to fund a limited number of large-scale fluid-flow (and heat-transfer) simulations in support of the aircraft industry's efforts to design better turbine engines. LSU's research office organized a meeting of (primarily engineering) faculty to see if a group could be put together to submit a viable research proposal to the DOE. I attended this meeting, just for grins; but it turned out to be a very smart decision. At the meeting, I met Sumanta Acharya (and Dimitris Nikitopoulos) and learned about his multidimensional simulations of incompressible fluids; he was looking for funding opportunities that would support his efforts to scale from 2D to 3D simulations. I also learned that he usually solved the Euler equations using a pressure-Poisson approach. We both realized that my group's successful implementation of a 3D Poisson solver (for gravity) on the MasPar could serve as an illustration of how his group could likely efficiently solve the pressure-Poisson equation in 3D. We wrote the proposal to DOE, and it was funded at $0.5 million. Thus began a very successful, multi-decade collaboration between my group and Sumanta's mechanical engineering group.
So … I am fairly confident that the approach you take to solve the gravitational-Poisson equation will help you understand how to solve the pressure-Poisson equation (or vise versa) on the finite-element grid. Note, however, that to my knowledge, Sumanta's simulations always involved a finite-difference, rather than a finite-element, methodology.
Recommended Riemann S-Type Ellipsoids for Modeling
Introductory Remarks
|
On 4 January 2023, Shawn Walker reintroduced the following strategy: "But if I remember correctly, I think the idea was to start with some baby steps. Perhaps have a fixed domain (the star) and solve the Euler equations in this with perhaps a fixed “fake” gravitational potential. Just to get something working. Then add the Poisson equation for the gravity, which would couple with the fluid." |
Joel's response: I am completely with you regarding the idea of starting with baby steps. But if we totally focus on Riemann S-Type ellipsoids, even the first few baby steps can be very realistic. Immediately below is a table that itemizes my recommendation regarding which ellipsoids should be modeled fist, second, third, etc. and why. What follows is a short preview.
Every S-Type configuration is a uniform-density ellipsoid (semi-axes: a, b, c) whose gravitational potential -- inside, outside, and on the surface of the ellipsoid -- is known analytically in terms of incomplete elliptic integrals of the 1st and 2nd kind (or simpler, trigonometric functions). When the chosen ellipsoid is viewed from a frame that is rotating (about its c-axis) with a characteristic frequency, , the ellipsoidal configuration appears stationary. As a result, the (analytically specified) gravitational potential does not vary with time. For our purposes, this can naturally serve as the "fixed fake" potential to which you refer.
As viewed from the proper () rotating frame, we also know the exact solution to the Euler equations throughout every S-Type ellipsoid. It is a steady-state flow in which all Lagrangian fluid elements move along closed elliptical orbits that …
- lie in planes parallel to the system's (a-b) equatorial plane;
- have identical ellipticities (that is, identical axis ratios, );
- have identical orbital frequencies.
So, as we try to build a code that can solve the Euler equations, we can (A) build a coordinate grid that is rotating with the desired () frequency; (B) "guess" a velocity flow-field that corresponds to what we know to be the correct, steady-state solution; (C) hold fixed the analytically known gravitational potential; (D) then use the code to integrate the Euler equations forward in time and see how well the configuration maintains a steady-state flow. We will have successfully debugged the "Euler equations" code if steady-state has been achieved for a variety of different Riemann S-Type ellipsoids.
Once the "Euler equations" code has been properly debugged, we can then add a Poisson solver; this will allow us to examine non-steady-state flows that result from natural instabilities among the set of Riemann S-Type ellipsoids.
Other useful attributes of Riemann S-Type ellipsoids …
- Each is a (incompressible) uniform-density ellipsoid with semi-axes, ; usually without loss of generality we are able to set .
- The steady-state velocity flow-field that is associated with each equilibrium configuration can be characterized by the values of two physical parameters: a frequency, , that is associated with the rate of the ellipsoidal figure's spin about its -axis; and, a vorticity, , associated with the elliptical orbital motion of Lagrangian fluid elements inside and on the surface of the ellipsoid, when viewed from a frame that is rotating with the frequency, .
Initial Equilibrium Configurations Recommended for Dynamical Analysis
(Axisymmetric) Maclaurin Spheroids
The following table lists four "critical points" drawn from Table 4 (Appendix A, p. 611) of 📚 Hachisu, Tohline, & Eriguchi (1987); go here for additional details.
|
RRSTEM Table 1 |
||||||||||||||||||||
|
Model |
|
|
|
|
Bifurcation Characteristics … |
|||||||||||||||
| †Geometric Distortion | Angular Mom. Profile | Instability Type | ||||||||||||||||||
|
A |
Uniform | Secular | ||||||||||||||||||
|
B |
Dynamical | |||||||||||||||||||
|
C |
Uniform | Secular | ||||||||||||||||||
|
D |
Dynamical | |||||||||||||||||||
|
†Following 📚 Y. Eriguchi & I. Hachisu (1985, A&A, Vol. 148, pp. 289 - 292) — see especially their Appendix and their Table 2 — is the Legendre polynomial. See also, p. 429 of 📚 J. M. Bardeen (1971, ApJ, Vol. 167, pp. 425 - 446). |
||||||||||||||||||||
|
Given the value of the eccentricity, , we immediately know from the accompanying detailed discussion that …
|
||||||||||||||||||||
Second-Harmonic Distortions
|
"The disturbances of the Maclaurin spheroids that belong to the second harmonics lead to instability for smaller values of the angular momentum than do those that belong to any higher harmonic … [Of] the five oscillation frequencies associated with these disturbances … one is able to distinguish two critical points … The first, when is 0.8127 — our Model A — is the point of bifurcation where the Maclaurin and Jacobi sequences intersect. Although σ2 vanishes at this critical point, it is positive on either side, so that instability does not set in here, at least in the absence of further effects. The second, when is 0.9529 — our Model B — represents the onset of [dynamical] instability, and also the most flattened Maclaurin spheroid that can lie on a Riemann sequence of type S …" |
|
— Drawn from pp. 475 - 476 of 📚 Lebovitz (1967) |
Model A:
|
This is the point along the Maclaurin spheroid sequence where the Jacobi sequence bifurcates. Some of the quantitative characteristics of this critical axisymmetric configuration are identified in Table IV (Chapter 6, §39, p. 103) of [EFE]. See also … the first line in Table B1 (p. 446) of 📚 Bardeen (1971); and Appendices D.3 & D.4 (pp. 485-486) of [T78]. |
| RRSTEM Figure 1 | |
|---|---|
|
EFE Diagram |
Ω2 vs. j2 Diagram |
|
Left panel: This version of the familiar EFE Diagram displays the horn-shaped region — bounded by the lower (LSA) and upper (USA) self-adjoint sequences — where all equilibrium, S-type Riemann ellipsoids reside. Axisymmetric , uniformly rotating equilibrium configurations belong to the Maclaurin spheroid sequence which, as indicated, functions as the right-hand vertical boundary of the EFE diagram. Maclaurin spheroids that have an eccentricity less than that of Model A lie along the blue segment of the sequence; the orange segment is populated by Maclaurin spheroids with eccentricities larger than that of Model A but less than that of Model B ; all other Maclaurin spheroids lie along the black segment. Right panel: The solid, multi-colored curve shows how the (square of the) dimensionless rotation frequency, , varies with the (square of the) dimensionless total angular momentum, , along the Maclaurin spheroid sequence. As in the accompanying (left panel) EFE diagram, Model A and Model B mark the ends of the differently colored curve segments. Both panels: A pair of small yellow circular markers identify the points where, respectively, the USA and LSA sequences intersect the Maclaurin spheroid sequence; and the small green square marker identifies where has its maximum value along the Maclaurin spheroid sequence. The sequence of uniformly rotating Jacobi ellipsoids is identified by the series of small solid purple markers; Model A is the axisymmetric equilibrium configuration at the point where the Jacobi ellipsoid sequence intersect (bifurcates from) the Maclaurin spheroid sequence. Similarly, Model B lies at the intersection of the LSA with the Maclaurin spheroid sequence. |
|
Model B:
|
From p. 141 of [EFE], we find that this model, "… the Maclaurin spheroid on the verge of dynamical instability, is the first member of the [Riemann S-type ellipsoid] self-adjoint sequence ." Some of the quantitative characteristics of this critical (axisymmetric) Maclaurin spheroid are identified in Table VI (Chapter 7, §48, p. 142) of [EFE]; for example, . In Table B1 (p. 446) of 📚 Bardeen (1971), this is referred to as the "First nonaxisymmetric dynamical instability." |
|
"… to what kind of configuration does [this] instability lead? 📚 Rossner (1967) has answered this question with the aid of Riemann's formulation of the nonlinear, ordinary differential equations describing the motion of a liquid ellipsoid. Integrating the equations numerically, Rossner found that the configuration neither gets disrupted nor finds its way to a new steady state, but performs a complicated unsteady motion." — See further reference to Rossner's work, below. |
|
— Drawn from pp. 475 - 476 of 📚 Lebovitz (1967) |
Ring-Like Distortions
Model C: (additional supporting discussion)
|
📚 Eriguchi & Sugimoto (1981) claim that the one-ring (Dyson-Wong toroid) sequence bifurcates from the Maclaurin sequence precisely at the point where the spheroid has an eccentricity, — in which case, also, and . In support of this conjecture, they point out that, 📚 S. Chandrasekhar (1967a, ApJ, Vol. 147, pp. 334 - 352) — referred to in [EFE] as Publication XXX — and 📚 Bardeen (1971) have shown that this is … a neutral point on the Maclaurin sequence against the perturbation of displacement at the surface where is one of the spheroidal coordinates." This is also the "neutral point" on the Maclaurin sequence labeled "F" in Table I of 📚 Hachisu & Eriguchi (1982); and the "bifurcation point" along the Maclaurin sequence that is labeled by the quantum numbers, in Table 1 of 📚 Hachisu & Eriguchi (1984) as well as in the inset box of the left panel of our RRSTEM Figure 2 (immediately below). See also … 📚 M. Ansorg, A. Kleinächter, & R. Meinel (2003, MNRAS, Vol. 339, Issue 2, pp. 515 - 523) |
| RRSTEM Figure 2 | |
|---|---|
|
Figure 1 extracted from §2.2, p. 488 of … |
|
 |
|
| An analogous illustration appears as Figure 1 (p. 585) of … I. Hachisu & Y. Eriguchi (1983) Bifurcations and Phase Transitions of Self-Gravitating and Uniformly Rotating Fluid Monthly Notices of the Royal Astronomical Society, Vol. 204, pp. 583 - 589 |
|
|
Left panel (primary plot): As in the right panel of RRSTEM Figure 1, above, the solid, multi-colored curve shows how varies with along the Maclaurin spheroid sequence. Models A and B are not explicitly labeled, but the plot still shows the small solid circular markers (purple and yellow, respectively) that identify the locations of these models on the spheroid sequence. The point where the Jacobi sequence bifurcates from the Maclaurin spheroid sequence (Model A) is labeled by the quantum numbers, , to indicate what geometric distortion, , that is associated with this particular bifurcation. Drawing from Table 1 of 📚 Hachisu & Eriguchi (1984), five other neutral points are marked by red crosses; three carry labels in this primary plot — — and the remaining two are labeled in the inset box — . Left panel (inset box): An inset box is used to magnify the segment of the Maclaurin spheroid sequence where bifurcation to the so-called one-ring (Dyson-Wong toroid) sequence occurs. The neutral point that is believed to be associated with the bifurcation point, itself, carries the geometric distortion label, , and is identified as our Model C. As has been detailed in our separate chapter discussion, the smooth (pink) curve that connects the spheroid sequence to the one-ring sequence has been defined by the set of 18 equilibrium models presented by 📚 Eriguchi & Sugimoto (1981); the set of small green square markers identify nine equilibrium models obtained from Table I of the separate study by 📚 Hachisu, Eriguchi, & Sugimoto (1982); and the small purple triangular markers identify eight equilibrium models obtained from Table Ia of 📚 Hachisu (1986a). Right panel: Figure 1 (plus caption) from 📚 Christodoulou, Kazanas, Shlosman, & Tohline (1995b) has been reprinted here to emphasize its similarity to, and overlap with our inset box. According to the caption of this reprinted figure, the filled circular marker labeled "A" identifies the bifurcation point on the Maclaurin spheroid sequence, where . Accordingly, we have annotated the reprinted figure to indicate that the axisymmetric equilibrium model associated with point "A" is exactly our Model C. As is stated in the caption of this reprinted figure, the dotted line XBC denotes the (hypothesized) onset of a secular instability that — in the nonlinear regime and conserving total angular momentum (vertical dotted line) — should deform the spheroid into a ring-like configuration. |
|
Model D:
|
First dynamical ring mode instability and bifurcation point to the Maclaurin toroid sequence. Also identified at as a bifurcation point in Table 2 (p. 292) of 📚 Eriguchi & Hachisu (1985). |
| RRSTEM Figure 3 | |
|---|---|
|
Figure 6 extracted from §4.2, p. 493 of … |
|
 |
|
|
Left panel (primary plot): The solid, multi-colored curve shows how (rather than ) varies with along the Maclaurin spheroid sequence. The positions of Models A, B, C and, now also, Model D along this sequence are labeled. The colors of the curve segments and the positions of the (yellow and purple) small circular markers have the same meanings as in RRSTEM Figure 1. The (pink curve) one-ring sequence from RRSTEM Figure 2 is also displayed. Left panel (inset box): An inset box is used to magnify the segment of the Maclaurin spheroid sequence where bifurcation to the so-called Maclaurin toroid sequence occurs. Three neutral points along the Maclaurin spheroid sequence are identified by light-green circular markers, and are labeled according to their respective geometric distortions — see Table 2 of 📚 Eriguchi & Hachisu (1985). They have argued that the neutral point that is associated with bifurcation, itself, carries the geometric distortion label, ; it has been identified here as our Model D. As has been detailed in our separate chapter discussion, the smooth (violet) curve that connects the spheroid sequence to the Maclaurin toroid sequence has been defined by the set of 15 equilibrium models presented by 📚 Eriguchi & Hachisu (1985) in their Table 2. [This data supersedes the modeling of the Maclaurin toroid sequence presented by 📚 Marcus, Press, & Teukolsky (1977) in their discovery paper.] Right panel: Figure 6 (plus caption) from 📚 Christodoulou, Kazanas, Shlosman, & Tohline (1995b) has been reprinted here to emphasize its similarity to, and overlap with our inset box. According to the caption of this reprinted figure, the filled circular marker labeled "A" identifies the point along the Maclaurin spheroid sequence where ; according to 📚 Bardeen (1971), this neutral point is associated with a P4 geometric distortion and should be associated with the onset of dynamical axisymmetric instability. 📚 Eriguchi & Hachisu (1985) agree that this is the eccentricity at which the P4 neutral point resides, but they argue that bifurcation — and onset of dynamical axisymmetric instability — should be associated instead with the P6 neutral point, as labeled in our inset box, because "P6" is encountered earlier than "P4" along the Maclaurin spheroid sequence. [As they argue, 📚 Bardeen (1971) misidentified the bifurcation point because he only investigated models undergoing a P4 distortion.] In accordance with the arguments of 📚 Eriguchi & Hachisu (1985), our choice for Model D is the Maclaurin spheroid whose eccentricity is the same as the P6 neutral point, that is, . |
|
Finite-Amplitude Oscillations of the Maclaurin Spheroid
In §53 (pp. 172 - 184) of [EFE] we find a discussion titled, "A class of finite-amplitude oscillations of the Maclaurin spheroid". The primary focus is on simulations presented by 📚 L. F. Rossner (1967, ApJ, Vol. 149, pp. 145 - 168) — referred to in [EFE] as Publication XXXVIII — which may provide excellent points of comparison for our own investigations into the oscillatory motions of initially stable — but perturbed — Maclaurin spheroids, and the nonlinear evolution of initially unstable Maclaurin spheroids.
Jacobi Ellipsoids
|
RRSTEM Table 2 |
||||||||||||||
|
Model |
|
|
|
|
|
Bifurcation Characteristics … |
||||||||
| †Geometric Distortion | Angular Mom. Profile | Instability Type | ||||||||||||
|
E |
Dumbbell-shaped | Uniform | Secular | |||||||||||
|
F |
Pear-shaped | Uniform | Secular | |||||||||||
|
Given the value of the square of the angular velocity, , we immediately know from the accompanying detailed discussion that …
|
||||||||||||||
Pear-Shaped Distortion
Model F:
|
According to Chapter 6, §40 of [EFE], a pear-shaped configuration bifurcates from the Jacobi Sequence at , where ; this result has been obtained via the virial relations — see Eq. (28) on p. 106 — as well as via a direct perturbation analysis — see Eq. (57) on p. 110. From the information provided in the first row of Table I in 📚 Eriguchi, Hachisu, & Sugimoto (1982), we appreciate as well that . (This information also has been recorded near the end of our accompanying discussion of the Jacobi ellipsoid sequence.) |
| RRSTEM Figure 4 | |
|---|---|
|
Primary plot: As in the right panel of RRSTEM Figure 1, above, the solid, multi-colored curve shows how varies with along the Maclaurin spheroid sequence; for reference, Model A and Model B are labeled. Also as in RRSTEM Figure 1, starting at the Model A bifurcation point, the purple dashed curve identifies the equilibrium sequence of Jacobi ellipsoids. A red cross labeled F identifies the position along the Jacobi ellipsoid sequence that is a "neutral point against the 3rd-order harmonic perturbation." A so-called pear-shaped sequence branches off at this point; here, we have displayed the behavior of this sequence by drawing the properties of equilibrium models from Table I (p. 1071) of 📚 Eriguchi, Hachisu, & Sugimoto (1982). Inset box: Especially Because the pear-shaped sequence is very short, an inset box is used to magnify the plotted sequence; this was also done by 📚 Eriguchi, Hachisu, & Sugimoto (1982) — see their Figure 1 (p. 1072). A red arrow, that accompanies our Model F label, points to the location along the Jacobi sequence where the relevant neutral point lies. As is suggested by 📚 Eriguchi, Hachisu, & Sugimoto (1982), the presumption is that this pear-shaped sequence bifurcates from the Jacobi sequence at the neutral point. But this is not the case in our plot. Upon closer inspection, we see that the pear-shaped sequence does appear to bifurcate from the Jacobi sequence in Figure 1 of 📚 Eriguchi, Hachisu, & Sugimoto (1982) and that this happens because the Jacobi sequence is shifted a bit from our depiction of the Jacobi sequence location. Curious! |
|
Dumbbell-Shaped Distortion
Model E:
- According to the last pair of equations on p. 128 of [EFE], Chapter 6, §45, a neutral point belonging to the fourth harmonic (a dumbbell-shaped) distortion arises on the Jacobi Sequence at and . Chronologically, this result for appears first in Eq. (93) on p. 635 of 📚 S. Chandrasekhar (1967b, ApJ, Vol. 148, pp. 621 - 644) — referred to in [EFE] as Publication XXXII. Then, in Eq. (66) on p. 302 of 📚 S. Chandrasekhar (1968, ApJ, Vol. 152, pp. 293 - 304) — referred to in [EFE] as Publication XXXV — we find , along with a footnote [5] which states, "The value found earlier differs slightly; but the difference is not outside the limits of accuracy of the numerical evaluation."
- According to the first row of properties in Table II of 📚 Eriguchi, Hachisu, & Sugimoto (1982), we find that Model E is characterized by the properties … ; ; and . I have not (yet) found the corresponding value of in any of Chandrasekhar's publications, but if we combine the value of obtained from EHS82 with the values of obtained from [EFE], we find … ; from the above expression, ; and . This value of is very close to the value obtained by EHS82.
- In the paragraph at the top of the right-hand column of p. 467 of 📚 I. Hachisu (1986b, ApJS, Vol. 62, pp. 461 - 499), we find … ; .
- 📚 D. M. Christodoulou, D. Kazanas, I. Shlosman, & J. E. Tohline (1995b, ApJ, Vol. 446, pp. 485 - 499) grab parameter values from a variety of sources. In subsection "B" (Jacobi Ellipsoid to Binary) of their Table 1 (p. 494) and in the first paragraph of their §3.2 (p. 492), they state … ; ; and, .
- NOTE (23 May 2023): Plugging the axis values from p. 128 of [EFE] — that is, — into our "Riemann01.for" application, we find , and , and .
| RRSTEM Figure 5 | |
|---|---|
|
Figure 4 extracted from §3.2, p. 493 of … |
|
 |
|
|
Left panel (primary plot): Same as the primary plot displayed in RRSTEM Figure 4, immediately above. A red cross labeled E identifies the position along the Jacobi ellipsoid sequence that is a neutral point against a 4th-order harmonic perturbation. A so-called dumbbell-shaped sequence branches off at this point; it, in turn, transitions to a sequence of equal-mass binaries. Left panel (inset box): An inset box shows more clearly the sequence of equilibrium models that make up the dumbbell (green markers and curve) and binary (blue markers and curve) sequences. Here, the dumbbell sequence is defined by a set of equilibrium models drawn from Table II (p. 1073) of 📚 Eriguchi, Hachisu, & Sugimoto (1982) while the binary sequence is defined by a set of equilibrium models drawn from the subsection (p. 243) of Table 1 labeled "N = 0" in 📚 Hachisu & Eriguchi (1984b). Right panel: Figure 4 (plus caption) from 📚 Christodoulou, Kazanas, Shlosman, & Tohline (1995b) has been reprinted here to emphasize its similarity to, and overlap with our inset box. According to the caption of this reprinted figure, the filled circular marker labeled "A" identifies the bifurcation point on the Jacobi ellipsoid sequence, where . Accordingly, we have annotated the reprinted figure to indicate that the Jacobi ellipsoid model associated with point "A" is exactly our Model E. As is stated in the caption of this reprinted figure, the dotted line XBC denotes the (hypothesized) onset of a secular instability that — in the nonlinear regime and conserving total angular momentum (vertical dotted line) — should lead to fission of the ellipsoid into an equal-mass binary system. |
|
Details
- Maclaurin Spheroid Sequence:
- Standard Presentation
- Alternate Sequence Diagrams
- Oblate-Spheroidal Coordinates
- Various Simple Rotation Profiles
- Two Particularly Relevant Angular Momentum Distributions
- Uniform Rotation → bifurcation leads to Dyson-Wong "one-ring" sequence
- → bifurcation leads to 📚 Marcus, Press, & Teukolsky (1977) "Maclaurin Toroid" sequence
- Eriguchi, Hachisu, and their various Colleagues
- Maclaurin Toroid Sequence (MPT77 & EH85)
- Phase Transition to Dyson-Wong (one-ring) sequence
|
See also our associated, more detailed discussion of Critical Points along the Maclaurin Spheroid Sequence. |
Lebovitz and Lifschitz
Invitation
|
On 8 May 2023, Stephen Sorokanich sent the following email to Joel: "Dr. Cohl and I are wondering if you would like to join our discussion of …" N. R. Lebovitz & A. Lifschitz (1996)
Short-Wavelength Instabilities of Riemann Ellipsoids Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences Vol. 354, Issue 1709, pp. 927 - 950 "This paper is very interesting to us because the authors consider Eulerian perturbations to the steady-state S-type ellipsoid velocity and pressure fields. The resulting linear equations in the Eulerian frame seem ideal for us to compare with our current finite element simulations of the nonlinear system. This is the only paper I've found by Lebovitz and Lifschitz where the stability analysis is carried out in an Eulerian frame. There's some nice analysis in the paper too. The linearized equations are solved using the "geometrical-optics approximation," which reduces the 3-dimensional linearized Euler equations to a system of ordinary differential equations. These solutions are used to draw conclusions for the stability of the S-type ellipsoids. Maybe there are other approximations to this system?" NOTE from Joel: The referenced paper is obviously related to the companion publication … N. R. Lebovitz & A. Lifschitz (1996) We have already prepared a MediaWiki chapter whose focus is on this "LL96" publication.
New Global Instabilities of the Riemann ellipsoids The Astrophysical Journal, Vol. 458, pp. 699 - 713 |
WKB (geometrical-optics) Method
As Stephen has pointed out, in 📚 Lebovitz & Lifschitz (1996b), the linearized equations are solved using the "geometrical-optics approximation." I am not familiar with this so-called "geometrical-optics" method, but in the last couple of paragraphs of §1 of their paper, LL96b refer to it also as the "WKB" approximation/method. I have been exposed to this alternate terminology; the WKB approximation has been used by astronomers in connection with efforts to understand the onset and development of "spiral-arm" structures in disk galaxies. Here is an excerpt from [BT87].
|
The Tight-Winding Approximation
§6.2.2 (p. 352) of [BT87] "… In the early 1960s a number of workers, notably A. J. Kalnajs, C. C. Lin, and A. Toomre, realized that for tightly wound density waves (i.e., waves whose radial wavelength is much less than the radius [of the galaxy's disk]) the long-range coupling [due to gravity] is negligible, the response is determined locally, and the relevant solutions are analytic. As we shall see, this tight-winding or WKB approximation† is an indispensable tool for understanding the origin and evolution of density waves in galaxies." †Named after the closely related Wentzel-Kramers-Brillouin approximation of quantum mechanics. |
Governing Linearized Equations
In our accompanying discussion we present a derivation of the …
| N. R. Lebovitz (1989a) The Stability Equations for Rotating, Inviscid Fluids: Galerkin Methods and Orthogonal Bases Geophysical & Astrophysical Fluid Dynamics, Vol. 46:4, pp. 221 - 243 | ||||||
|
Mixed Lagrangian/Eulerian Representation
| ||||||
When rewritten with an alternate set of variable notations — specifically, — and recognizing that , this key relation becomes,
| N. R. Lebovitz & A. Lifschitz (1996) Short-Wavelength Instabilities of Riemann Ellipsoids Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences Vol. 354, Issue 1709, pp. 927 - 950 | ||||||
| ||||||
Next, following LL96b, we let each variable be represented by the sum of an unperturbed, steady-state component (subscript zero) and a small perturbation,
| (i.e., remains unchanged) | ||
where is a characteristic length scale. As a result, we have,
|
|
|
|
Then, subtracting off the unperturbed steady-state component, namely,
|
|
|
|
we obtain,
|
|
|
|
Finally, dividing thru by ,
|
|
|
|
and adopting the characteristic timescale, , we have the dimensionless Euler equation,
|
|
|
|
|
📚 Lebovitz & Lifschitz (1996b), §2, p. 929, Eqs. (2.4) & (2.7) |
||
See Also
- MediaWiki chapter on Riemann S-Type Ellipsoids <== includes Self-Adjoint Data Table from EFE and from Howard's high-precision (20-digit accuracy) evaluation.
- MediaWiki chapter on Lebovitz & Lifschitz (1996) <== Analytic expressions that give the location of the Self-Adjoint Sequences in the EFE Diagram is presented here.
- 📚 S. Ou, J. E. Tohline, & P. M. Motl (2007, ApJ, Vol. 665, pp. 1074 - 1083), titled, Further Evidence for an Elliptical Instability in Rotating Fluid Bars and Ellipsoidal Stars.

|
|---|
|
Appendices: | VisTrailsEquations | VisTrailsVariables | References | Ramblings | VisTrailsImages | myphys.lsu | ADS | |